MAPLE
Геометрические объекты
Задание матриц
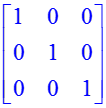
Для работы с матрицами в первую очередь необходимо ввести сроку with(linalg): (она подгрузит в Maple библиотеку функций линейной алгебры). Матриц задаются функцией «matrix». Элементы матрицы перечисляются в квадратных скобках через запятую, каждую строку так же заключают в квадратные скобки. Например: > with(linalg): > matrix([[1,0,0],[0,1,0],[0,0,1]]); > matrix([[1,2,3],[4,5,6],[7,8,9]]);

Арифметические действия
Сложение и вычитание матриц производится обычными «+» и «–», а умножение — «&*». В отличие от обычных действий, при работе с матрицами все вычисления проводятся «в уме». Для вывода результата на экран используется функция «evalm»: > A:=matrix([[1,–2],[1,3]]); B:=matrix([[–2,0],[–1,1]]); > evalm(A)+evalm(B)=evalm(A+B); > evalm(A)*evalm(B)=evalm(A&*B);
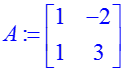
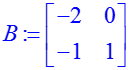
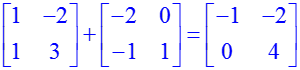
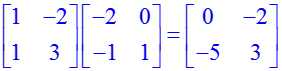
Детерминант, обратная и транспонированная матрицы
Вычисление детерминанта матрицы осуществляется с помощью функции «det»: > A:=matrix([[1,–2],[1,3]]); Det(evalm(A))=det(A); Обратная матрица вычисляется функцией «inverse»: > evalm(A)^(–1)=inverse(A); Транспонирование производится функцией «transpose»: > evalm(A)^t=transpose(A);
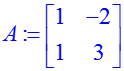
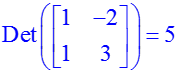
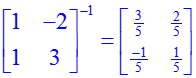
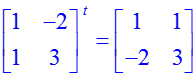
Характеристический полином, собственные значения матрицы
Характеристический полином вычисляется функцией «charpoly». Для наглядности можно отобразить характеристическую матрицу: > A:=matrix([[2,–2],[–1,3]]); > Det(evalm(A–lambda))=charpoly(A,lambda); Найдём собственные значения, решив уравнение det(A – λI) = 0: > charpoly(A,lambda)=0; solve(charpoly(A,lambda)); или с помощью функции «eigenvalues»: > eigenvalues(A);
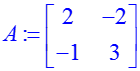
Обратите внимание, Maple вычи-сляет характеристический поли-ном как det(λI – A). Поэтому для нечётных размеров матриц пе-ред ним следует ставить «–».
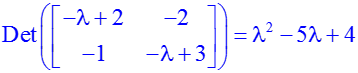
![]()
![]()
![]()
Собственные векторы матрицы
Собственные векторы матрицы вычисляются функцией «eigenvectors»: > A:=matrix([[2,–2],[–1,3]]); > eigenvectors(A); Расшифровывается это следующим образом. Собственное значение «4» имеет алгебраическую кратность 1 и соответствующий ему собственный вектор [–1, 1], аналогично, собственное значение «1» имеет алгебраическую кратность 1 и собственный вектор [2, 1]. Можно проверить:
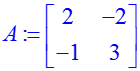
![]()
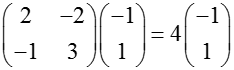
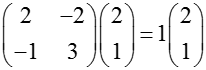
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.