ПРОИЗВОДНАЯ. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ. КАСАТЕЛЬНАЯ
Рассмотрим такую задачу. Пусть нам известен закон
движения движущегося вдоль прямой тела ![]() .
Нужно найти скорость движения тела в момент времени t.
.
Нужно найти скорость движения тела в момент времени t.
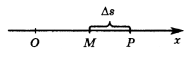 Предположим,
что в момент времени t тело находилось в точке M (см. рис.).
Дадим аргументу t приращение Δt и рассмотрим ситуацию в момент
времени t + Δt. Координата тела стала другой, оно будет
находиться в точке P. Значит, за время Δt тело переместилось из
точки M в точку P, т. е. прошло путь MP. Обозначим этот
путь Δs.
Предположим,
что в момент времени t тело находилось в точке M (см. рис.).
Дадим аргументу t приращение Δt и рассмотрим ситуацию в момент
времени t + Δt. Координата тела стала другой, оно будет
находиться в точке P. Значит, за время Δt тело переместилось из
точки M в точку P, т. е. прошло путь MP. Обозначим этот
путь Δs.
Нетрудно найти среднюю скорость ![]() движения тела за промежуток времени
движения тела за промежуток времени ![]() :
:
![]() .
.
А что такое скорость ![]() в момент времени t (ее называют мгновенной
скоростью)? Можно сказать так: это средняя скорость движения за промежуток
времени
в момент времени t (ее называют мгновенной
скоростью)? Можно сказать так: это средняя скорость движения за промежуток
времени ![]() при условии, что Δt выбирается все
меньше и меньше; иными словами, при условии, что
при условии, что Δt выбирается все
меньше и меньше; иными словами, при условии, что ![]() . Это значит, что
. Это значит, что ![]() . Подводя итог решению задачи, получаем
. Подводя итог решению задачи, получаем
![]() .
.
Решение задачи привело к математической модели — пределу отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю. Многие задачи физики, химии, экономики и т. д. приводят в процессе решения к такой же модели. Значит, эту математическую модель надо специально изучить, т. е.:
а) присвоить ей новый термин;
б) ввести для нее обозначение;
в) исследовать свойства новой модели.
Функция называется дифференцируемой в точке ![]() , если существует предел
, если существует предел ![]() . Величина этого
предела называется производной функции в точке
. Величина этого
предела называется производной функции в точке ![]() и обозначается
и обозначается![]() .
.
Найдем производные следующих функций по определению:
1.
Вычислите производную функции ![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
Ответ: ![]() .
.
2.
Вычислите производную функции ![]() .
.
![]() ,
, ![]() ,
, 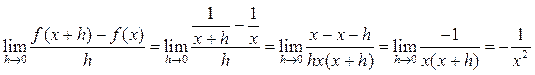 .
.
Ответ: 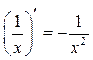 .
.
3.
Вычислите производную функции ![]() .
.
![]() ,
, ![]() .
.
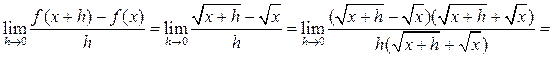
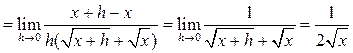 .
.
Ответ: 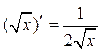 .
.
|
Частный случай |
||
|
|
|
|
|
|
|
|
|
|
|
|
![]() ,
,
![]() ,
,
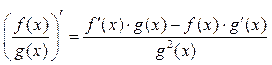 .
.
4.
Найдите производную функции ![]() .
.
![]() .
.
5.
Найдите производную функции ![]() .
.
![]() .
.
6.
Найдите производную функции ![]() .
.
![]() .
.
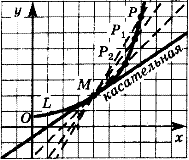
Касательные к графику функции
 Пусть
дана кривая (см. рис.), на ней выбрана точка M. Возьмем ещё одну точку
этой кривой — точку P. Проведем секущую MP. Далее будем
приближать точку P к точке M. Секущая MP будет
поворачиваться вокуруг точки M. Предельное положение секущей называют
касательной к кривой в точке M.
Пусть
дана кривая (см. рис.), на ней выбрана точка M. Возьмем ещё одну точку
этой кривой — точку P. Проведем секущую MP. Далее будем
приближать точку P к точке M. Секущая MP будет
поворачиваться вокуруг точки M. Предельное положение секущей называют
касательной к кривой в точке M.
Пусть через точку ![]() ,
в которой функция
,
в которой функция ![]() дифференцируема,
требуется провести касательную, ее уравнение
дифференцируема,
требуется провести касательную, ее уравнение ![]() ,
где k — угловой коэффициент прямой, равный тангенсу угла ее
наклона к оси абсцисс, b — ордината точки пересечения с осью Oy.
,
где k — угловой коэффициент прямой, равный тангенсу угла ее
наклона к оси абсцисс, b — ордината точки пересечения с осью Oy.
Уравнение касательной, проходящей через заданную точку
![]() , таково:
, таково: ![]() . Но как «увидеть» это
уравнение, в чём его геометрический смысл? Во-первых полезно убедиться, что это
уравнение прямой. Перепишем уравнение в виде
. Но как «увидеть» это
уравнение, в чём его геометрический смысл? Во-первых полезно убедиться, что это
уравнение прямой. Перепишем уравнение в виде ![]() . Таким образом,
переменная y линейно зависит от x, следовательно, точки с
координатами
. Таким образом,
переменная y линейно зависит от x, следовательно, точки с
координатами ![]() , удовлетворяющими
уравнению, лежат на прямой. Эта прямая проходит через точку
, удовлетворяющими
уравнению, лежат на прямой. Эта прямая проходит через точку ![]() , так как
, так как ![]() при
при ![]() . Ее угловой
коэффициент равен
. Ее угловой
коэффициент равен ![]() , тангенс
угла наклона секущей
, тангенс
угла наклона секущей ![]() . Поэтому
при
. Поэтому
при ![]() мы получим производную
функции
мы получим производную
функции ![]() в точек
в точек ![]() по самому ее
определению:
по самому ее
определению: ![]() . Значит,
наша прямая — касательная.
. Значит,
наша прямая — касательная.
7. Напишите
уравнение касательной к графику функции ![]() , проходящей через
точку графика с абсциссой 1.
, проходящей через
точку графика с абсциссой 1.
Решение:
![]() ,
, ![]() ,
, ![]() .
.
Таким образом, уравнение касательной имеет вид:
![]()
![]() .
.
Ответ: ![]() .
.
8. Напишите
уравнение касательной к графику функции ![]() ,
проходящей через точку графика с абсциссой
,
проходящей через точку графика с абсциссой ![]() .
.
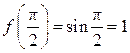 ,
, ![]() ,
, 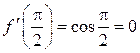 .
.
Таким образом, уравнение касательной имеет вид:
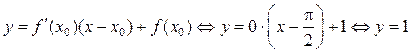 .
.
Ответ: ![]() .
.
См. ридер «Производные и интегралы».
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.