MAPLE
Решение дифференциальных уравнений
Решение дифференциальных уравнений (часть 1)
Для начала вспомним, что для вычисления обычных и частных производных в Maple используется команда «diff» («Diff»). С её помощью можно задать дифференциальное уравнение. Например, уравнения y’ = 2x + 3, y’ = y, y’’ + y = 0 записываются так: > Diff(y(x),x)=2*x+3; > Diff(y(x),x)=y(x); > Diff(y(x),x,x)+y(x)=0;
![]()
![]()
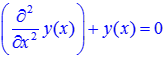
Решение дифференциальных уравнений (часть 2)
Решает дифференциальные уравнения функция «dsolve». У этой функции два аргумента: первый — дифференциальное уравнение, второй — функцию, относительно которой решается это уравне-ние. Решим, например, уравнения y’ = 2x + 3, y’ = y, y’’ + y = 0: > dsolve(diff(y(x),x)=2*x+3, y(x)); > dsolve(diff(y(x),x)=y(x), y(x)); > dsolve(diff(y(x),x,x)+y(x)=0, y(x)); где _С1 и _С2 — произвольные постоянные.
![]()
![]()
![]()
Решение дифференциальных уравнений (часть 3)
При наличии начальных условий, они записываются через запя-тую вместе с уравнением в фигурных скобках. Решим, например, уравнения с начальными условиями: y’ = 2x + 3, y(1) = 1; y’ = y, y(0) = 2; y’’ + y = 0, y(0) = 3, y’(0) = –1: > dsolve({diff(y(x),x)=2*x+3, y(1)=1}, y(x)); > dsolve({diff(y(x),x)=y(x), y(0)=2}, y(x)); > dsolve({diff(y(x),x,x)+y(x)=0, y(0)=3, D(y)(0)=–1}, y(x)); Обратите внимание на запись условия y’(0) = –1.
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.