ЧИСЛОВЫЕ МНОЖЕСТВА, СЧЕТНОСТЬ МНОЖЕСТВА РАЦИОНАЛЬНЫХ
ЧИСЕЛ,
ДОКАЗАТЕЛЬСТВО СУЩЕСТВОВАНИЯ ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ
Среди числовых множеств выделяют:
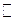 —
множество натуральных чисел 1, 2, 3, …
—
множество натуральных чисел 1, 2, 3, …
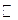 —
множество целых чисел … –2, –1, 0, 1, 2, …
—
множество целых чисел … –2, –1, 0, 1, 2, …
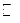 — множество рациональных
чисел — множество дробей вида
— множество рациональных
чисел — множество дробей вида 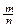 ,
где
,
где 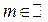 ,
, 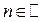 .
.
Ir — множество иррациональных чисел.
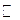 — множество
вещественных чисел.
— множество
вещественных чисел.
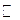 — множество
комплексных чисел.
— множество
комплексных чисел.
Любое рациональное число представляется в виде
бесконечной десятичной периодической дроби и наоборот, любая из таких дробей —
рациональное число.
Примеры (делим «в столбик»):
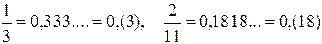
Примечание. Период правильной дроби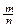 не
будет длиннее n, и при реализации алгоритма деления «в столбик» начнется не позже, чем через nшагов деления. Поясним это утверждение:
при делении числителя на знаменатель дроби n может получиться не
больше чем n различных остатков, поэтому не позже чем через n делений остатки начнут повторяться, причем повторяться циклически. Это
и даст период дроби.
не
будет длиннее n, и при реализации алгоритма деления «в столбик» начнется не позже, чем через nшагов деления. Поясним это утверждение:
при делении числителя на знаменатель дроби n может получиться не
больше чем n различных остатков, поэтому не позже чем через n делений остатки начнут повторяться, причем повторяться циклически. Это
и даст период дроби.
Пример обратного преобразования.Переведем в обычную дробь бесконечную десятичную периодическую дробь
0,(3)=0,333…
x =
0,333…
10х = 3,333…
9х = 3
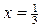 .
.
Теорема. Множество рациональных чисел
счетно.
Доказательство. Представим множество всех рациональных чисел в виде
бесконечной таблицы.
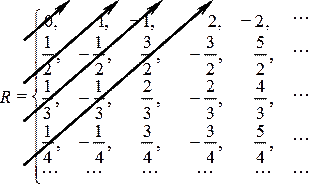 Укажем,
как строятся строки этой таблицы.
Укажем,
как строятся строки этой таблицы.
Первая строка: все целые числа, расположенные
по возрастанию их модуля и так, что знаки «+» и «–» чередуются.
Вторая строка: все несократимые дроби со знаменателем
2, расположенные по возрастанию их модуля и так, что знаки «+» и «–»
чередуются.
Третья строка: все несократимые дроби со знаменателем
3, расположенные по возрастанию их модуля и так, что знаки «+» и «–»
чередуются.
Вообще, n-я строка это все несократимые
дроби со знаменателем n, расположенные по возрастанию их модуля и так,
что знаки «+» и «–» чередуются.
Очевидно, что в этой таблице находятся все
рациональные числа. Используя прием диагонализации представим 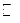 в виде:
в виде:
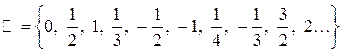 .
.
Так как 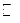 представилось
в форме последовательности, то есть его элементы можно занумеровать
устанавливается биекция между рациональными и натуральными числами. Это и означает,
что
представилось
в форме последовательности, то есть его элементы можно занумеровать
устанавливается биекция между рациональными и натуральными числами. Это и означает,
что 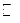 — счетное
множество.
— счетное
множество.
Иррациональные числа
Иррациональные числа — те, которые не могут быть записаны в виде отношения
целого к натуральному; не представляются в виде бесконечной периодической
десятичной дроби.
Вопрос о существовании иррациональных чисел
требует доказательства. В истории математики, например, число π
долгое время считалось частным двух натуральных чисел.
Теорема. Иррациональные
числа существуют.
Доказательство. (Метод от противного). Пусть 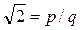 , где
, где 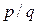 —
несократимая дробь.
—
несократимая дробь.
Тогда 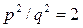 , откуда p2 = 2q2. Это значит, что квадрат числа p — четное число, тогда само p
тоже четное число.
, откуда p2 = 2q2. Это значит, что квадрат числа p — четное число, тогда само p
тоже четное число.
Если это так, то можно положить p =
2m, тогда равенство p2 = 2q2 можно представить в виде (2m)2 = 2q2 или 4m2 = 2q2, 2m2 = q2. Это означает, что q делится на 2, значит, q —
четное число, тогда можно положить q = 2r.
Тем самым получено, что p =
2m , а q = 2r , но тогда 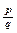 — сократимая
дробь. Противоречие.
— сократимая
дробь. Противоречие.
Итак, есть числа не представимые в виде
отношения целого к натуральному.
Поскольку иррациональные числа существуют, но
не записываются в виде периодической десятичной дроби, они записываются в виде
бесконечной десятичной непериодической дроби.
Все бесконечные дроби (периодические и
непериодические вместе) образуют множество вещественных (или действительных)
чисел:
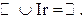
Заметим, что справедливо вложение:
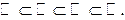
См. также приложение Ozes-World Home Page.
![]() — множество
вещественных чисел.
— множество
вещественных чисел.![]() — множество
комплексных чисел.
— множество
комплексных чисел.![]()
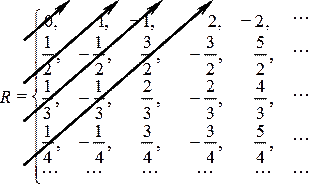 Укажем,
как строятся строки этой таблицы.
Укажем,
как строятся строки этой таблицы.![]() в виде:
в виде: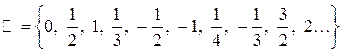 .
.![]() представилось
в форме последовательности, то есть его элементы можно занумеровать
устанавливается биекция между рациональными и натуральными числами. Это и означает,
что
представилось
в форме последовательности, то есть его элементы можно занумеровать
устанавливается биекция между рациональными и натуральными числами. Это и означает,
что ![]() — счетное
множество.
— счетное
множество.![]()