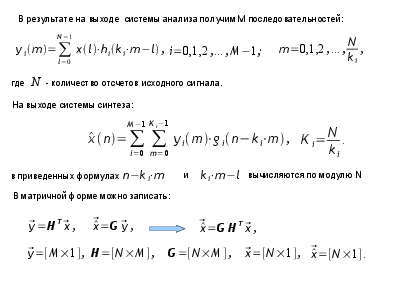


























Сжатие сигналов МТКС. Преобразования сигналов
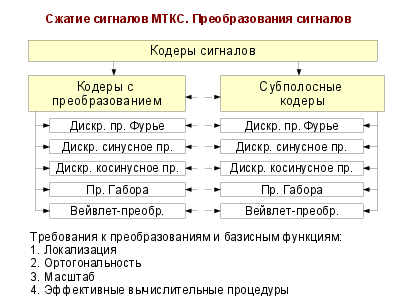
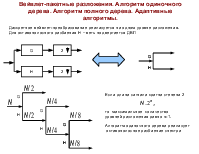
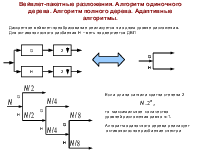
Кодеры сигналов
Кодеры с Субполосные преобразованием кодеры
 Дискр. пр. Фурье Дискр. пр. Фурье
Дискр. синусное пр. Дискр. синусное пр.
Дискр. пр. Фурье Дискр. пр. Фурье
Дискр. синусное пр. Дискр. синусное пр.
Дискр. косинусное пр. Дискр. косинусное пр.
Пр. Габора Пр. Габора
Вейвлет-преобр. Вейвлет-преобр.
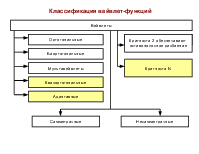
Требования к преобразованиям и базисным функциям:
1. Локализация
2. Ортогональность
3. Масштаб
4. Эффективные вычислительные процедуры
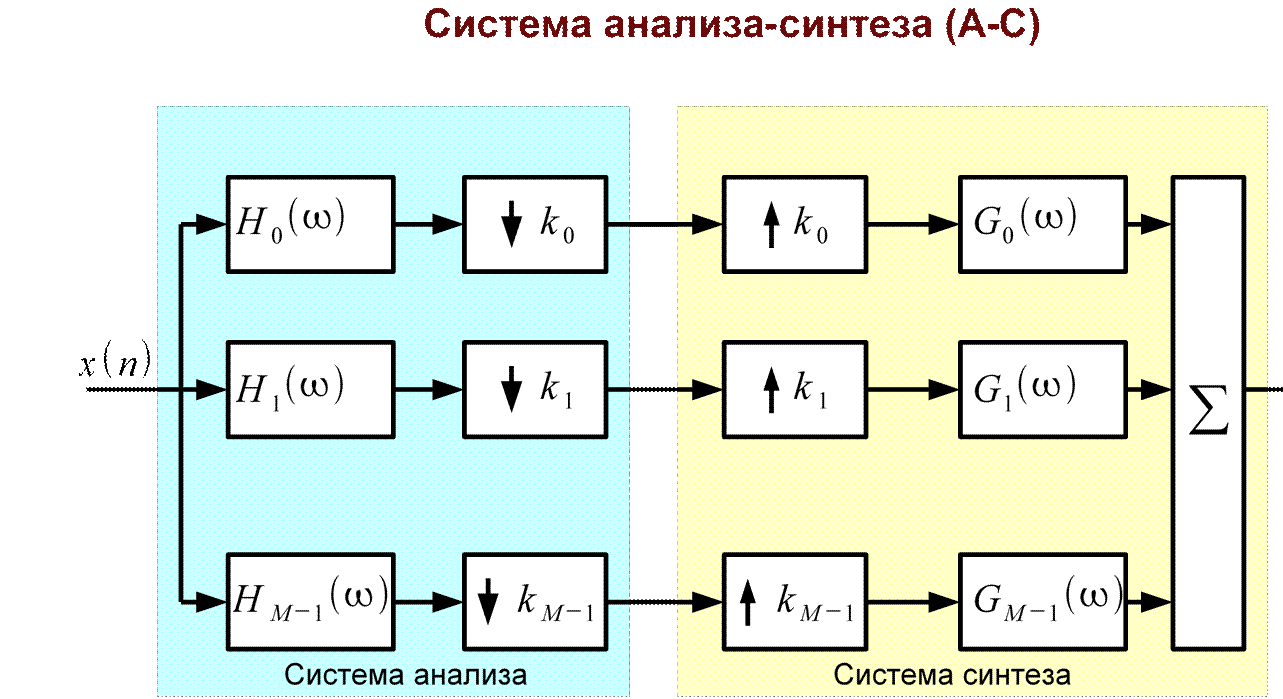
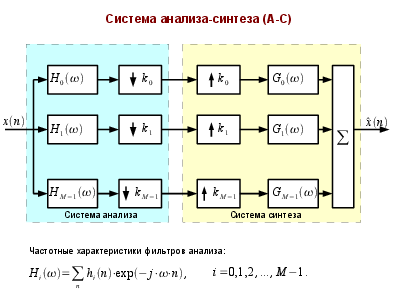
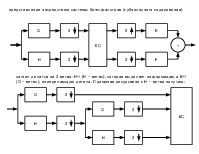
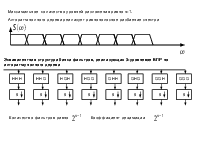
Частотные характеристики фильтров анализа:
H i =∑ hi n⋅exp− j⋅⋅n, i=0,1,2 ,... ,M−1.
n
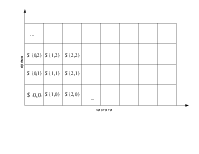
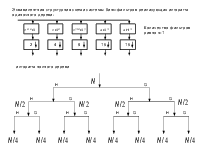
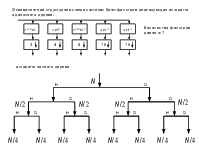
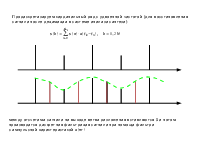
В результате на выходе системы анализа получим M последовательностей:
y im=N∑l=−01 xl⋅hiki⋅m−l, i=0,1,2 ,... ,M−1; m=0,1,2 ,... ,kNi ,
где N - количество отсчетов исходного сигнала.
На выходе системы синтеза:
M−1 K i−1 x n=∑i=0 m∑=0 yim⋅g in−ki⋅m, K i=kNi .
в приведенных формулах n−ki⋅m и ki⋅m−l вычисляются по модулю N
В матричной форме можно записать:
y=HTx, x=G
y, ![]() x=G
HTx,
x=G
HTx,
y=[M×1], H=[N×M ], G=[N×M ], x=[N×1], x=[N×1].
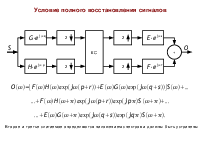
Для того чтобы система А-С обладала свойством полного восстановления необходимо:
x=x, ![]() G
HT=I.
G
HT=I.
если H - квадратная, то G=H−1T ; если H - не квадратная, то G=HHT−1H. если преобразование ортогональное, то HHT=HTH=I ,
H – квадратная
Тогда в случае полного восстановления H=G.
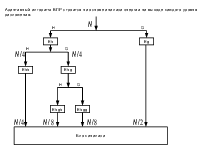
Фильтры анализа А-С системы производят октавополосное разбиение спектра

Ортогональные преобразования. Дискретное преобразование Фурье (ДПФ,DFT).
Пара преобразований Фурье в непрерывной форме:
S 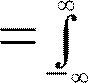 st⋅exp−j⋅⋅tdt
; st
st⋅exp−j⋅⋅tdt
; st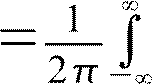 S ⋅exp j⋅⋅td.
S ⋅exp j⋅⋅td.
В дискретной форме:
|
S k=n∑=0 sn⋅exp−j2⋅N⋅n⋅k; |
k=0,1,2 ,... ,N−1 |
|
sn=N1 N∑−1 S k⋅exp j 2⋅N⋅n⋅k; |
n=0,1,2 ,... ,N−1 |
k=0
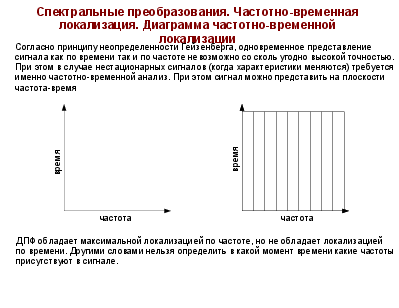
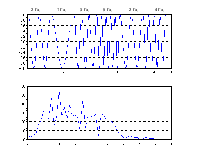
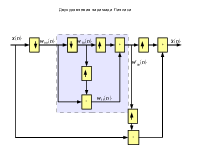
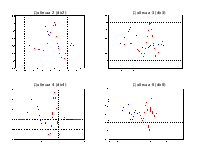
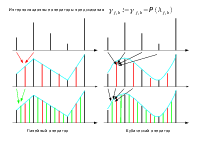
Согласно принципу неопределенности Гейзенберга, одновременное представление сигнала как по времени так и по частоте невозможно со сколь угодно высокой точностью. При этом в случае нестационарных сигналов (когда характеристики меняются) требуется именно частотно-временной анализ. При этом сигнал можно представить на плоскости частота-время

частота частота
ДПФ обладает максимальной локализацией по частоте, но не обладает локализацией по времени. Другими словами нельзя определить в какой момент времени какие частоты присутствуют в сигнале.
Оконные преобразования Фурье в непрерывной форме:
S
,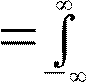 s t⋅wt−exp−j⋅⋅tdt
;
s t⋅wt−exp−j⋅⋅tdt
;
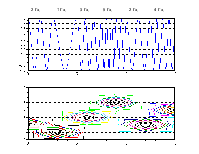
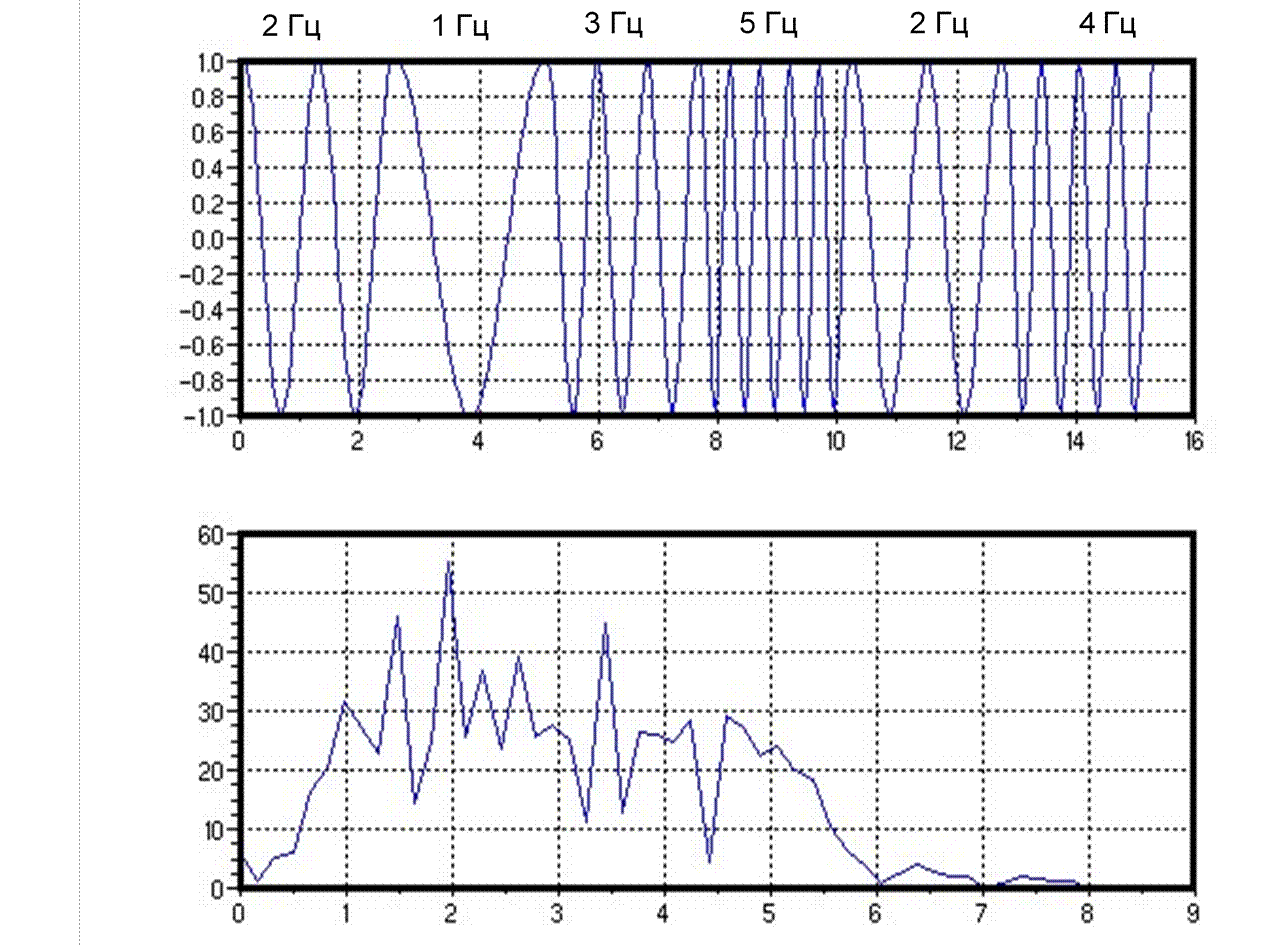
Оконные преобразования Фурье в дискретной форме:
S k=Nn∑=−01 sn⋅wn−m⋅exp−j 2⋅N⋅n⋅k;
k=0,1,2 ,... ,N−1 m=0,1,2 ,... ,M−1
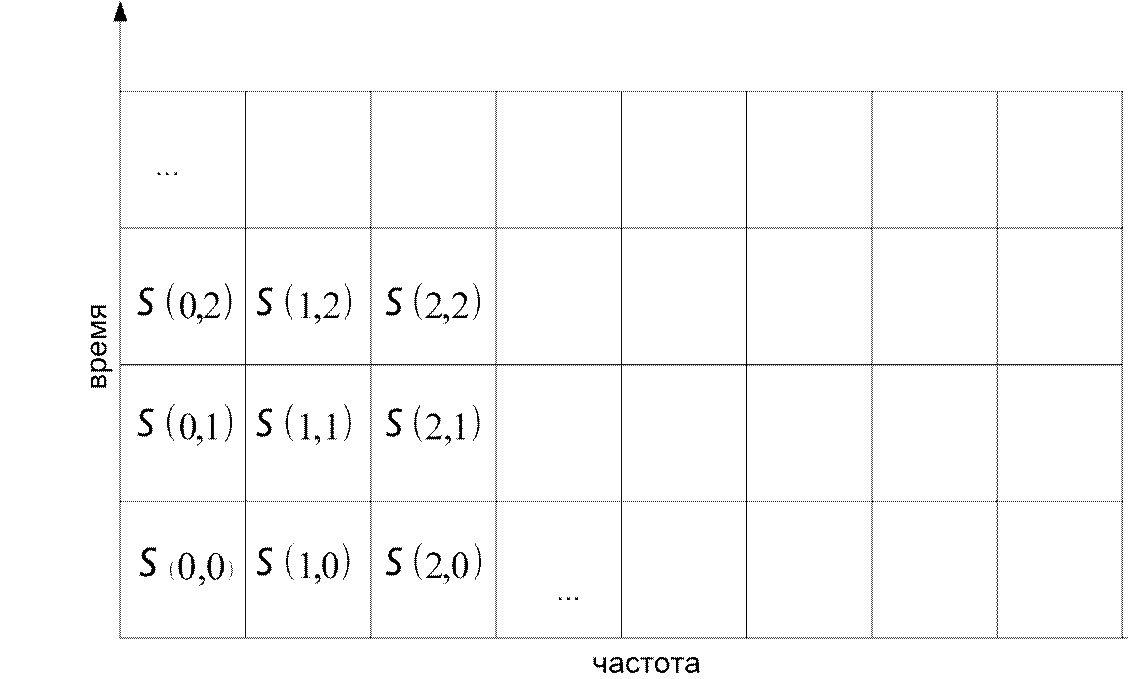
 3
Гц 5 Гц 2
Гц 4 Гц
3
Гц 5 Гц 2
Гц 4 Гц
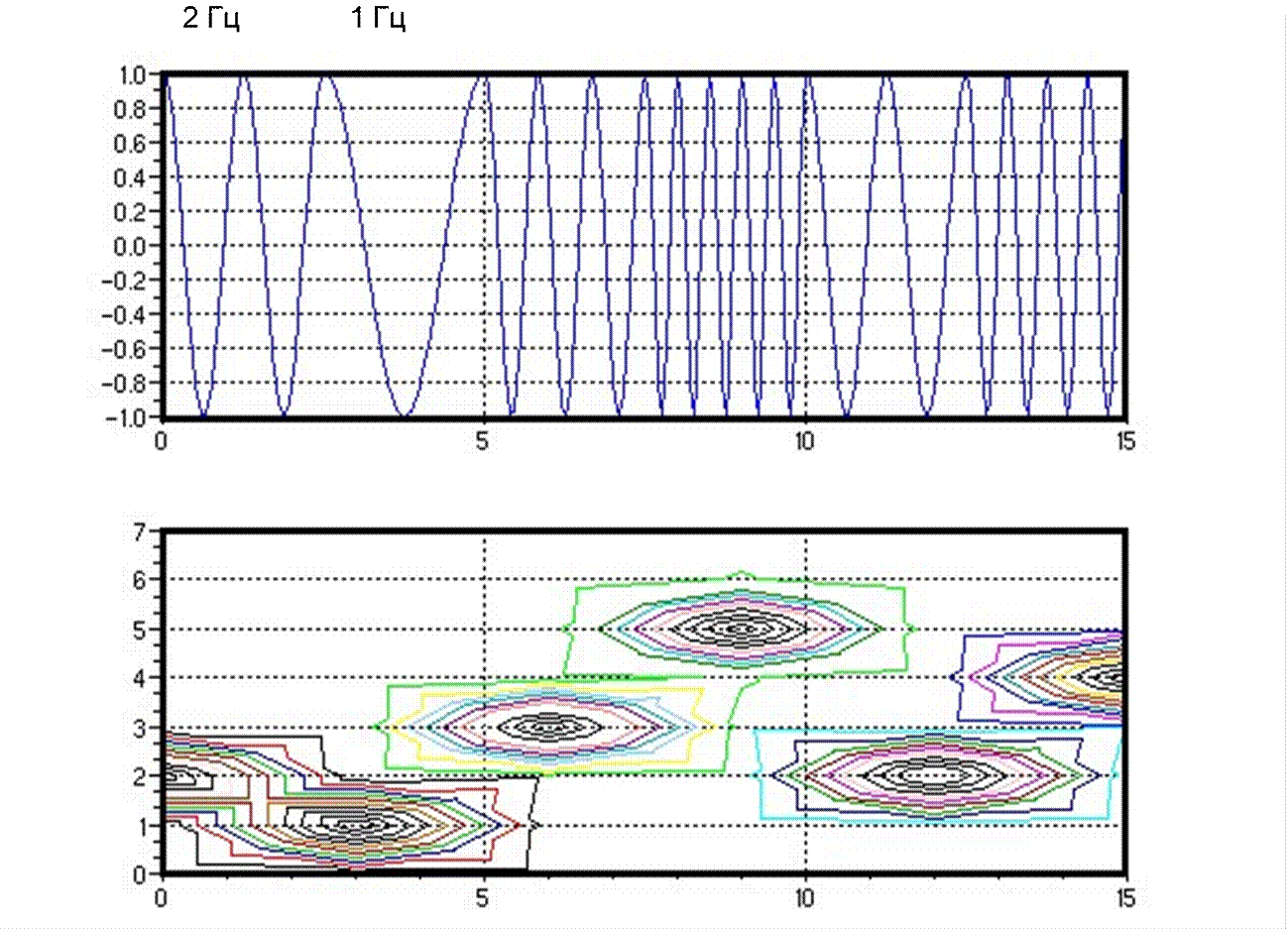
Преобразование Габора
Оконные преобразования Фурье
S ,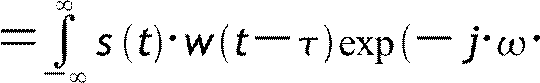 tdt
;
tdt
;
S k ,m=Nn∑=−01 s n⋅wn−m⋅exp−j 2⋅N⋅n⋅k;
k=0,1,2 ,... ,N −1 m=0,1,2 ,... ,M−1
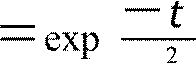 2
2
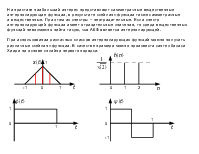
wt
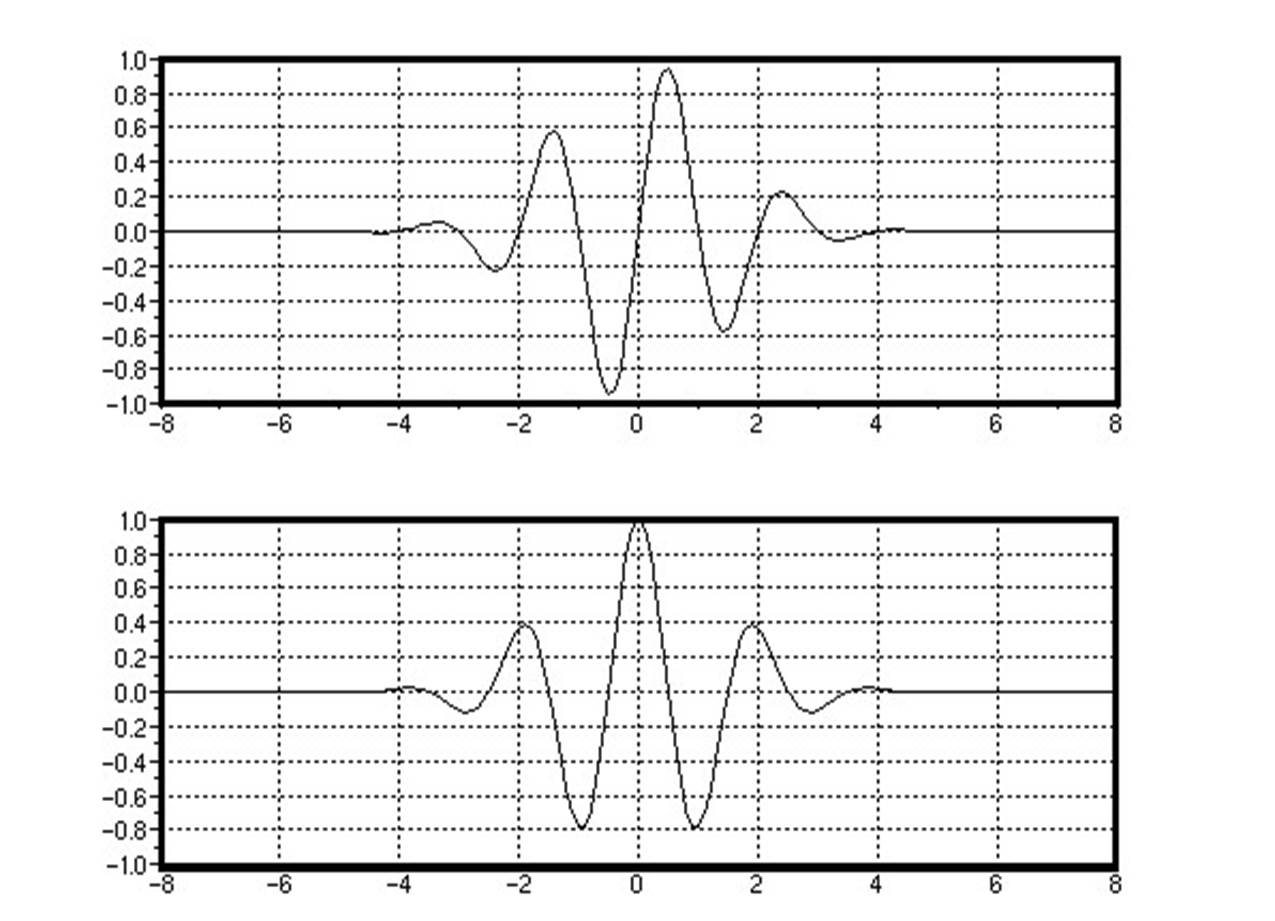
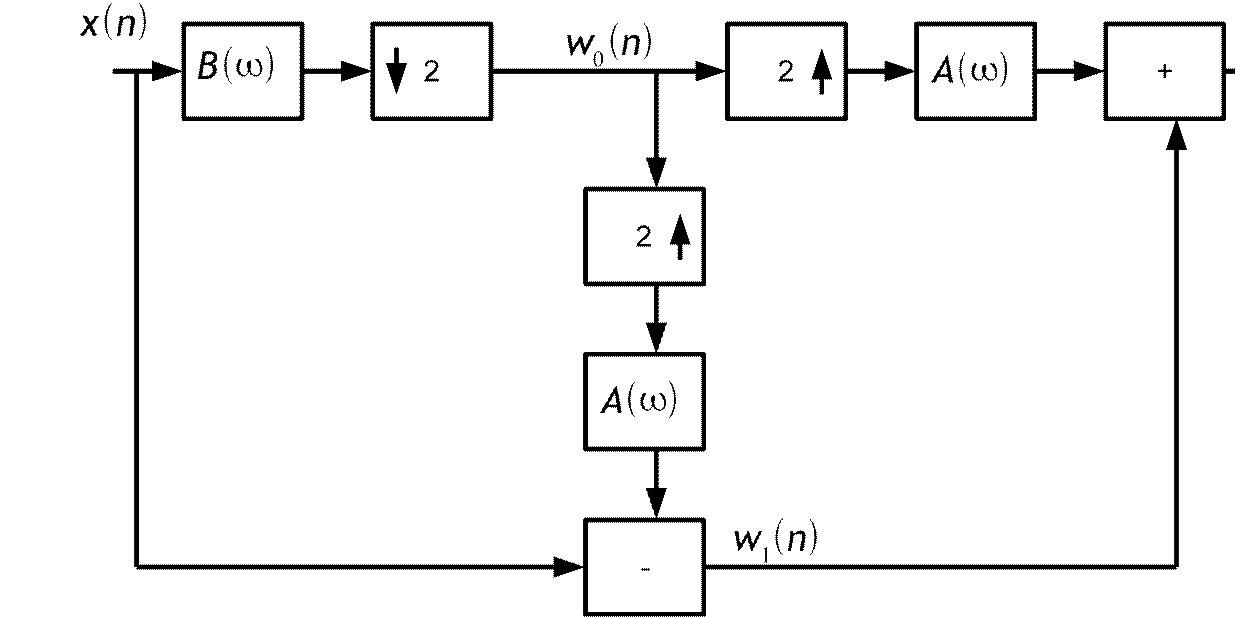
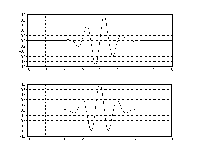
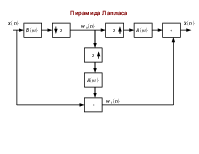
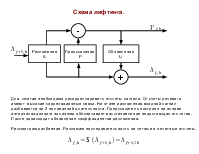
Двухуровневая пирамида Лапласа
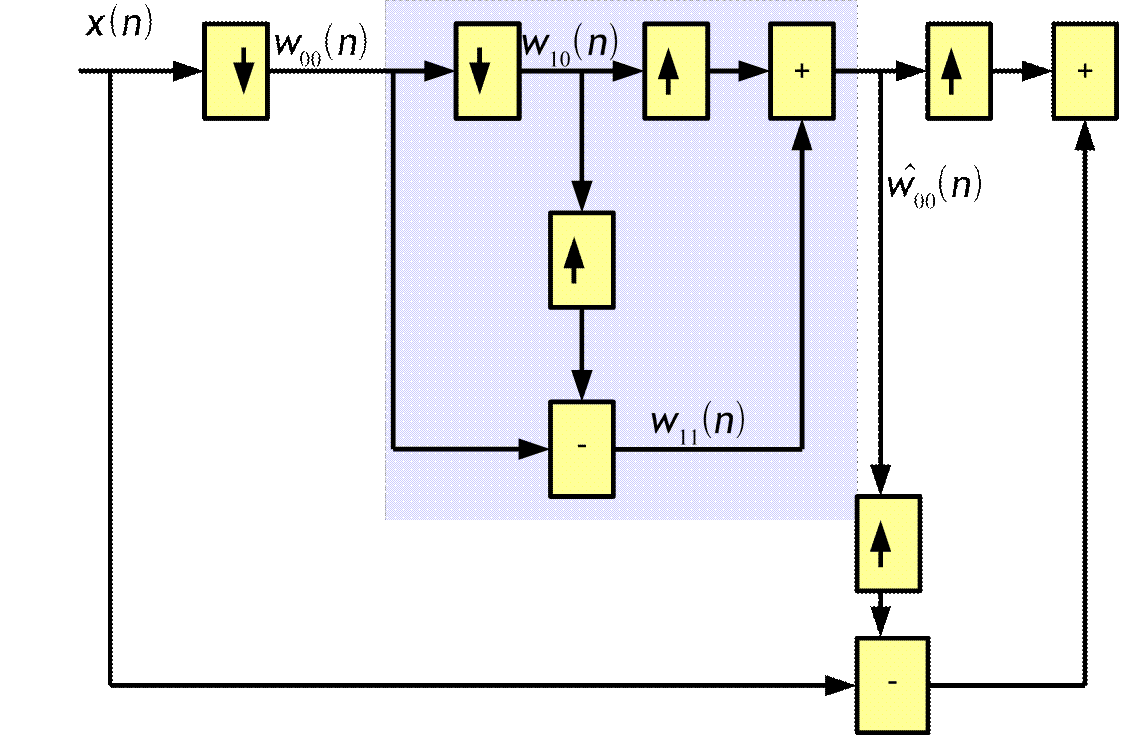

2
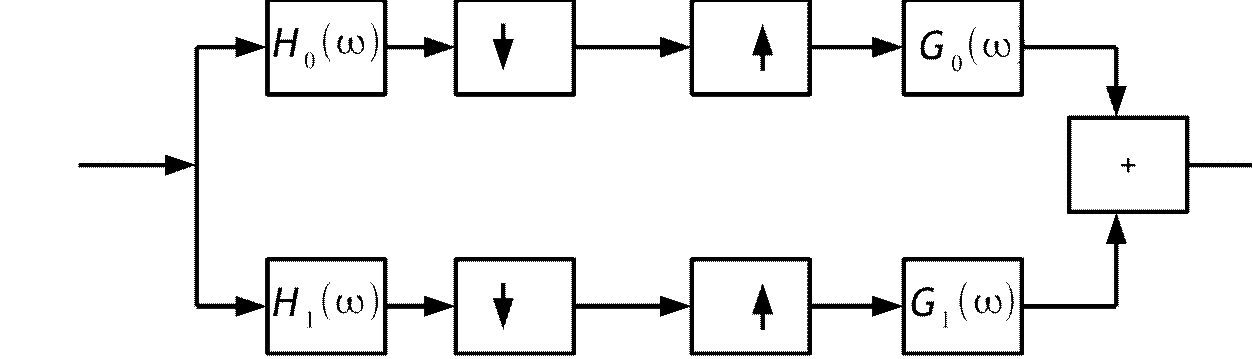
X 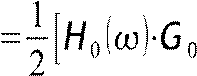 H1⋅G1]⋅X
...
H1⋅G1]⋅X
...
(*)
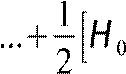 ⋅G0 H1⋅G1]⋅X
⋅G0 H1⋅G1]⋅X
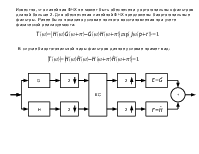
Второе слагаемое выражения (*) характеризует наложение спектров. Потребуем чтобы
H0=G0−=F ,
H1=G1−=exp j⋅F −,
тогда X 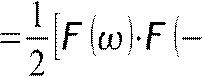 F
−⋅F
−]⋅X
...
F
−⋅F
−]⋅X
...
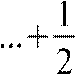 [F ⋅F
−exp jF
−⋅F
]⋅X
[F ⋅F
−exp jF
−⋅F
]⋅X
c учетом exp j=−1
X 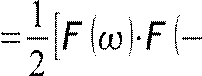 F
−⋅F
−]⋅X
.
F
−⋅F
−]⋅X
.
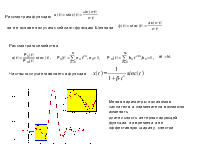
т.о. элайзинг на выходе системы ликвидирован, однако в каждой из полос он остался. конструирование КЗФ сводится к расчету НЧ фильтра с ЧХ удовлетворяющей
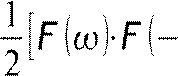 F
−⋅F
−]=1,
∣F
∣2∣F
∣2=2.
F
−⋅F
−]=1,
∣F
∣2∣F
∣2=2.
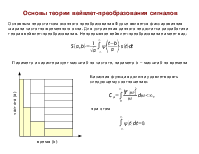
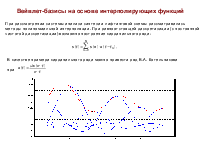
Основы теории вейвлет-преобразования сигналов
Основным недостатком оконного преобразования Фурье является фиксированная ширина частотно-временного окна. Для устранения данного недостатка разработана теория вейвлет-преобразования. Непрерывное вейвлет-преобразование имеет вид:
S
a,b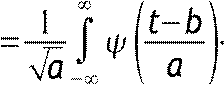 stdt
stdt
Параметр а характеризует масштаб по частоте, параметр b – масштаб по времени
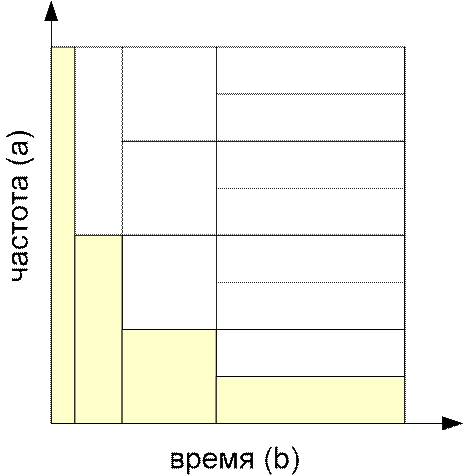 Базисная функция
должна удовлетворять следующему соотношению:
Базисная функция
должна удовлетворять следующему соотношению:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.