...F H exp jprexp jpS ...
...E G exp jqsexp jqS .
Второе и третье слагаемое определяются наложением спектров и должны быть устранены.
Если pr=qs, а также F =G , E =−H ,
в этом случае, сумма второго и третьего слагаемых равна 0
Рассмотрим первое слагаемое как комплексный коэффициент передачи:
T =[H G −G H ]exp jpr=1.
|
L если
длина фильтра H и G – четная, то p= 2 |
L g= 2 |
|
L если длина фильтра H и G – нечетная, то p= 2 |
L g= 2 |
При этом безошибочное восстановление достигается если коэффициенты фильтра G возьмем равными коэффициентам фильтра H, записанными в обратном порядке, и через один умноженными на -1: h=[h0 h1 h2 h3 h4 h5]; g=[h5 −h4 h3 −h2 h1 −h0].
Расчет фильтров с полным восстановлением. Фильтры Добеши. Биортогональные фильтры.
Ранее было показано, что для полного восстановления необходимо выполнение условия
M Tj⋅M j=I, (*)
![]() в случае фильтра
четвертого порядка:
в случае фильтра
четвертого порядка:
M j=h2 h3 0 0 0 0 h0 h1 ] h0 h1 h2 h3 0 0 0 0 0 0 h0 h1 h2 h3 0 0 0 0 0 0 h0 h1 h2 h3
h3 −h2 h1 −h0 0 0 0 0 0 0 h3 −h2 h1 −h0 0 0 0 0 0 0 h3 −h2 h1 −h0 h1 −h0 0 0 0 0 h3 −h2
Из уравнения можно записать h20h12h22h23=0.5; h0 h22h1 h3=0.
таким образом, уравнение (*) имеет множество количество решений. Для единственности наложим дополнительные ограничения: h3−h2h1−h0=0; 0⋅h3−1⋅h22⋅h1−3⋅h0=0;
тогда можно записать коэффициенты H фильтра (коэффициенты масштабирующего уравнения для скейлинг функции) :
![]()
![]()
![]() h=[13
,
33
,
h=[13
,
33
,
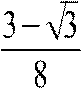 ,
, 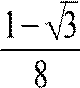 ]
]
полученный базис является базисом Добеши 4 порядка. Аналогично можно получить базисы Добеши произвольного порядка, с учетом ограничений на нулевые моменты.
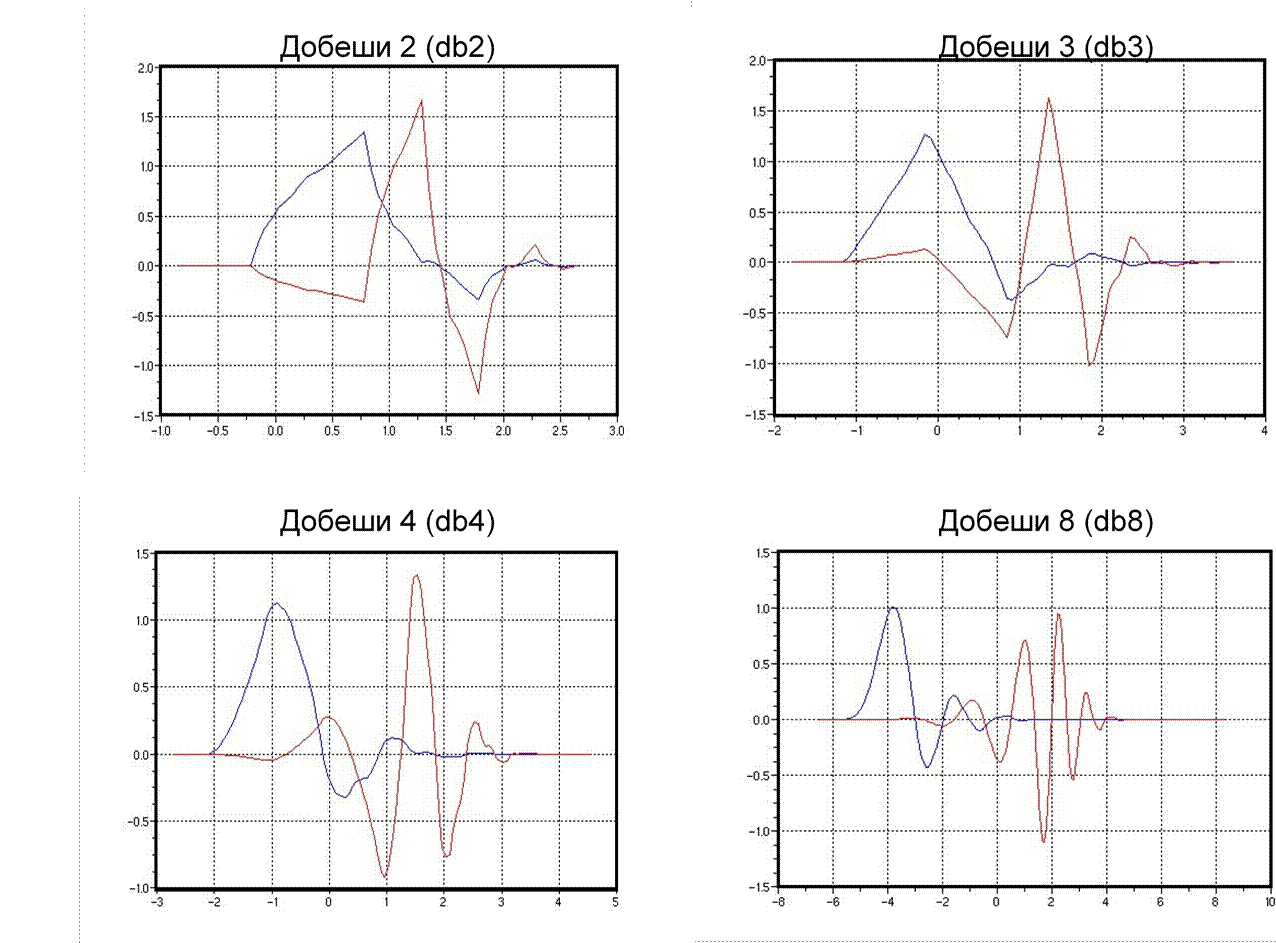
Известно, что линейная ФЧХ не может быть обеспечена у ортогональных фильтров длиной больше 2. Для обеспечения линейной ФЧХ предложены биортогональные фильтры. Ранее было показано условие полного восстановления при учете физической реализуемости:
T =[H G −G H ]exp jpr=1.
В случае биортогональной пары фильтров данное условие примет вид:
∣T ∣=∣HH −H H ∣=1.
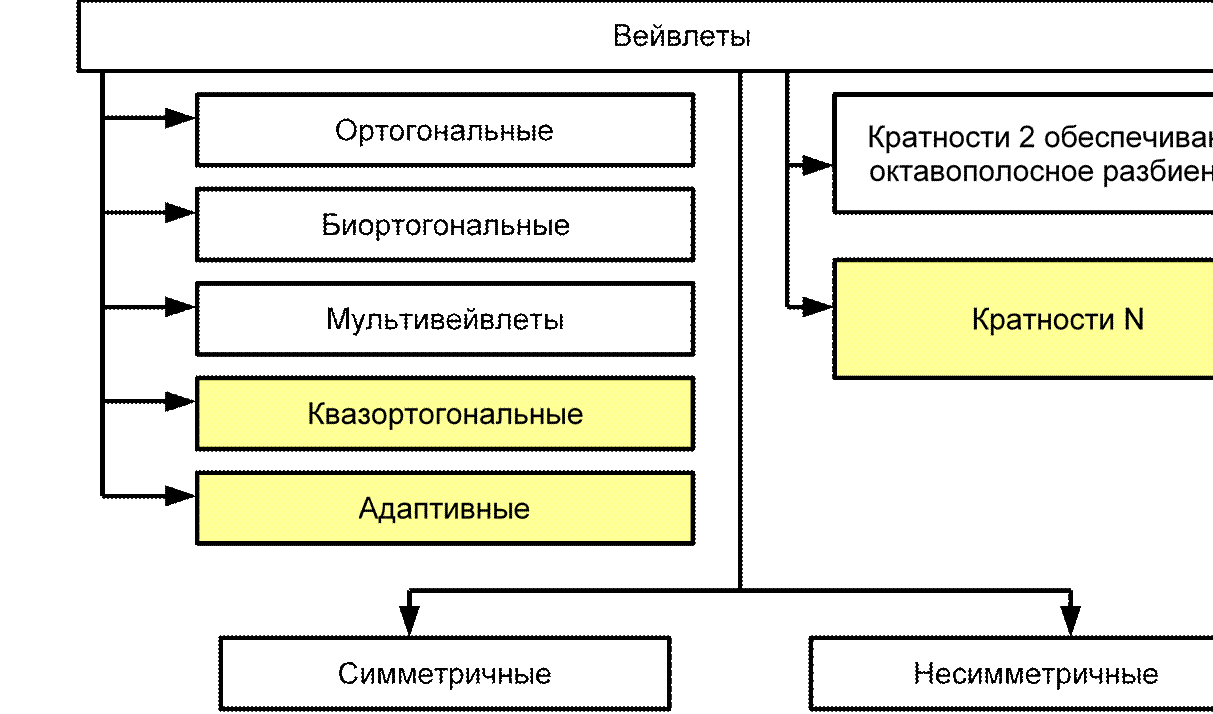
Основные классы вейвлет-функций представлены в таблице
|
НАЗВАНИЕ БАЗИСА |
Тип |
|
1. Хаара |
Ортогональное |
|
2. Добеши |
Ортогональное |
|
3.Шеннона |
Ортогональное |
|
4. Мейера |
Ортогональное |
|
5. Коэна-Добеши-Фово |
Биортогональное |
|
6. Виллансенора |
Биортогональное |
|
7. Койфмана |
биортогональное |
Вейвлет-пакетные разложения. Алгоритм одиночного дерева. Алгоритм полного дерева. Адаптивные алгоритмы.
Дискретное вейвлет-преобразование реализуется на одном уровне разложения.
Для октавополосного разбиения H – веть подвергается ДВП

![]() Если
длина сигнала кратна степени 2
Если
длина сигнала кратна степени 2
N =2n ,
то максимальное количество уровней разложения равно n-1.
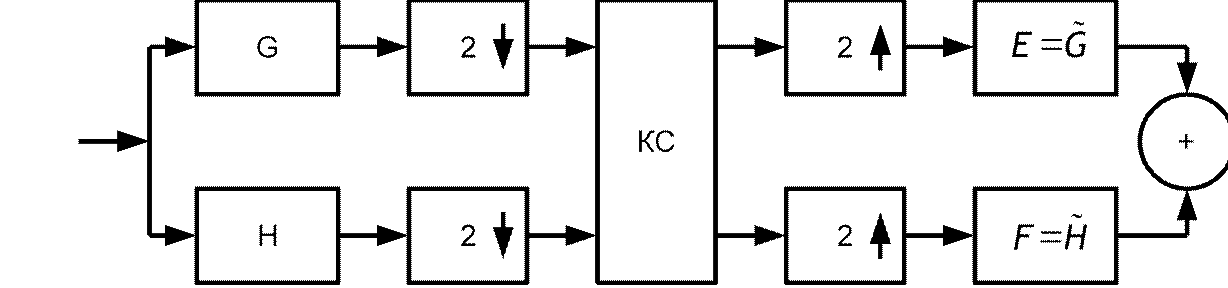
Алгоритм одиночного дерева реализует октавополосное разбиение спектра Эквивалентная структурная схема системы банк-фильтров реализующих алгоритм одиночного дерева:
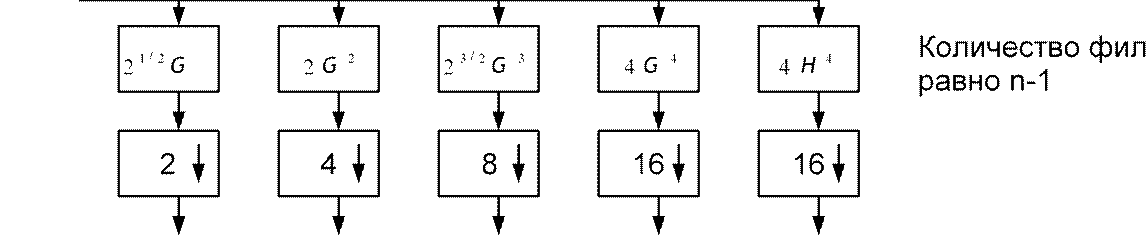
Максимальное количество уровней разложения равно n-1.
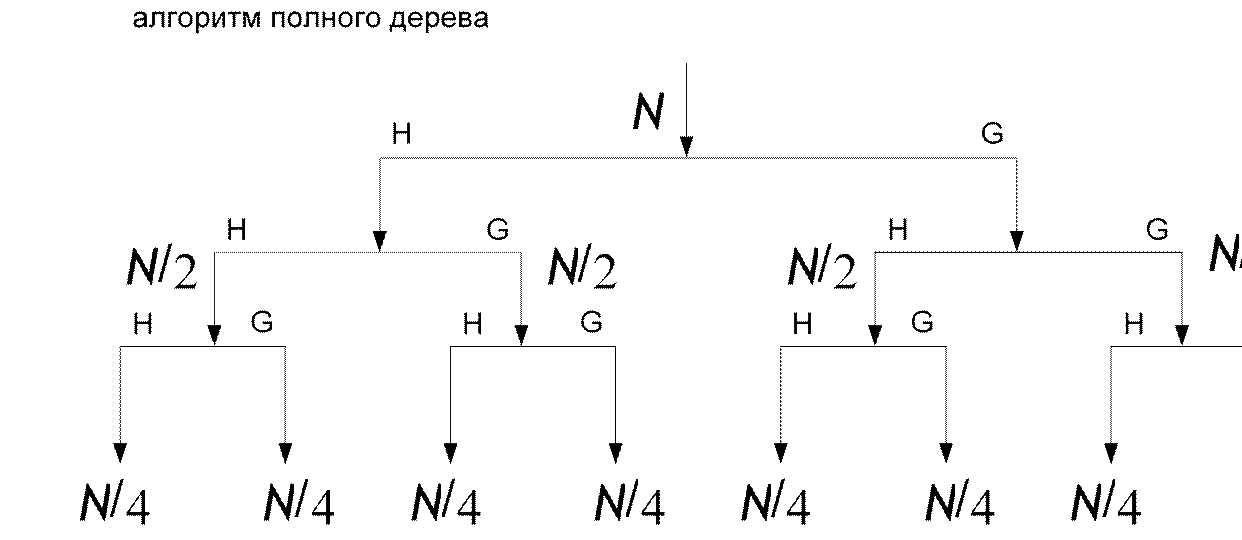
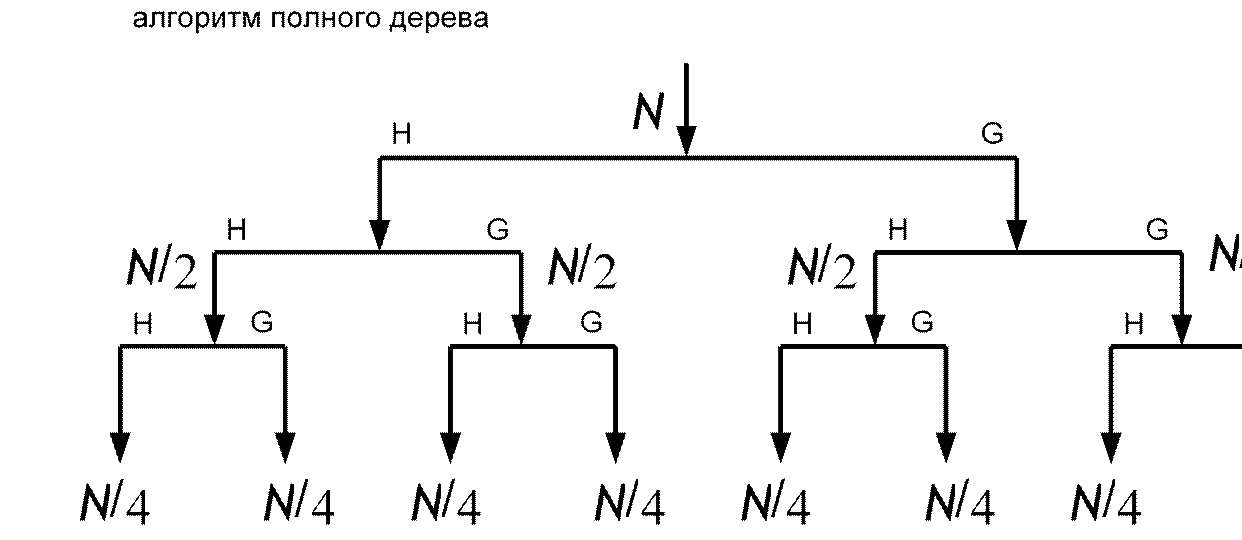
Алгоритм полного дерева реализует равнополосное разбиение спектра

Эквивалентная структура банка фильтров, реализующих 3-уровневое ВПР по алгоритму полного дерева
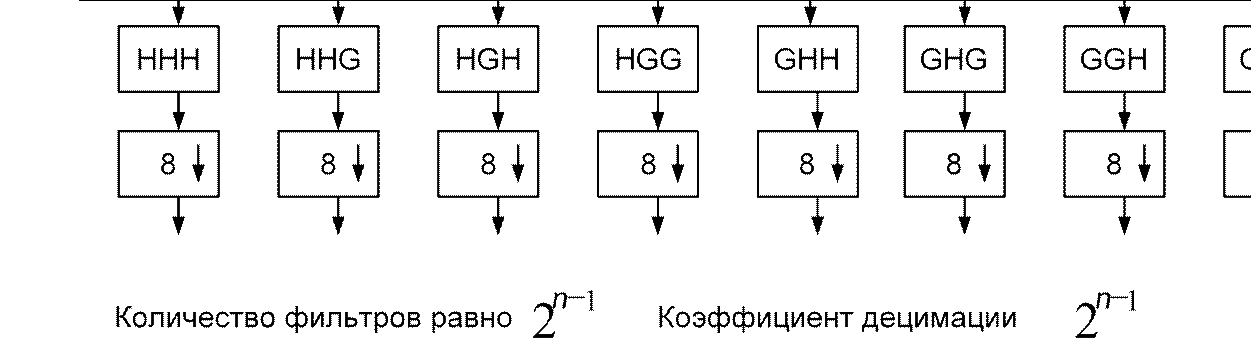
Вейвлет-пакетные разложения. Алгоритм одиночного дерева. Алгоритм полного дерева. Адаптивные алгоритмы.
Дискретное вейвлет-преобразование реализуется на одном уровне разложения.
Для октавополосного разбиения H – веть подвергается ДВП

![]() Если
длина сигнала кратна степени 2
Если
длина сигнала кратна степени 2
N =2n ,
то максимальное количество уровней разложения равно n-1.
Алгоритм одиночного дерева реализует октавополосное разбиение спектра Эквивалентная структурная схема системы банк-фильтров реализующих алгоритм одиночного дерева:

Максимальное количество уровней разложения равно n-1.
Алгоритм полного дерева реализует равнополосное разбиение спектра

Эквивалентная структура банка фильтров, реализующих 3-уровневое ВПР по алгоритму полного дерева

Адаптивный алгоритм ВПР строится на основе анализа энергии на выходе каждого уровня разложения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.