Сжатие сигналов МТКС. Преобразования сигналов. Кодеры с Субполосные преобразованием кодеры, страница 4

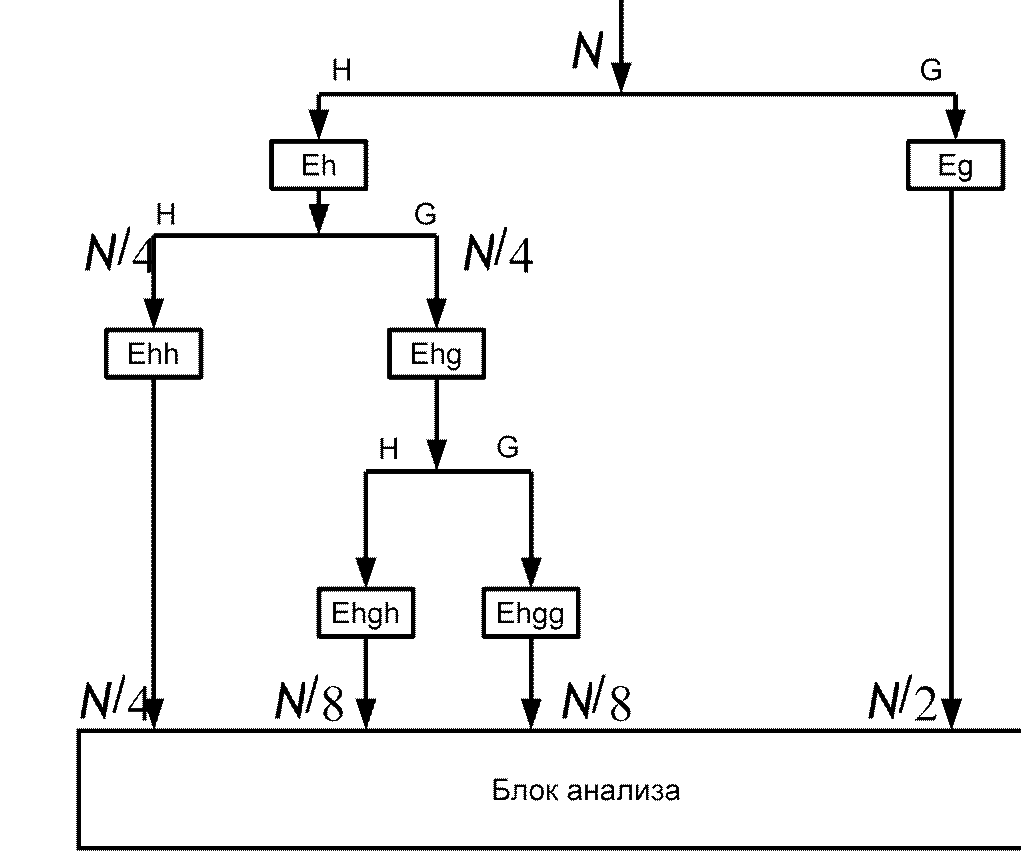
Эквивалентная структурная схема банк-фильтров:

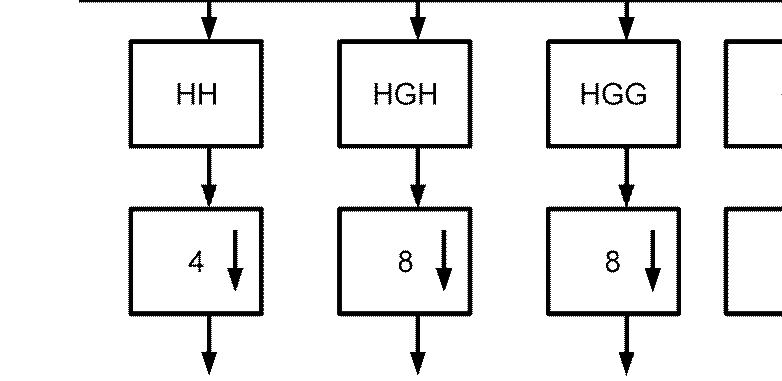
в этом случае производится адаптивное разбиение спектра:

Для  сжатия необходимо декорреллировать отсчеты сигнала. Отсчеты речевого имеют  высокие корреляционные связи. На этапе разложения входной сигнал разбивается на 2 половинной длительности. Предсказатель построен на основе интерполяционного полинома обеспечивает восстановление недостающих отсчетов. После происходит обновление коэффициентов разложения.

Рассмотрим разбиение. Разложим последовательность на четные и нечетные отсчеты.

j,k=S j1,k=j1,2k

Интерполяционные операторы предсказания j,k :=j,k−P j,k

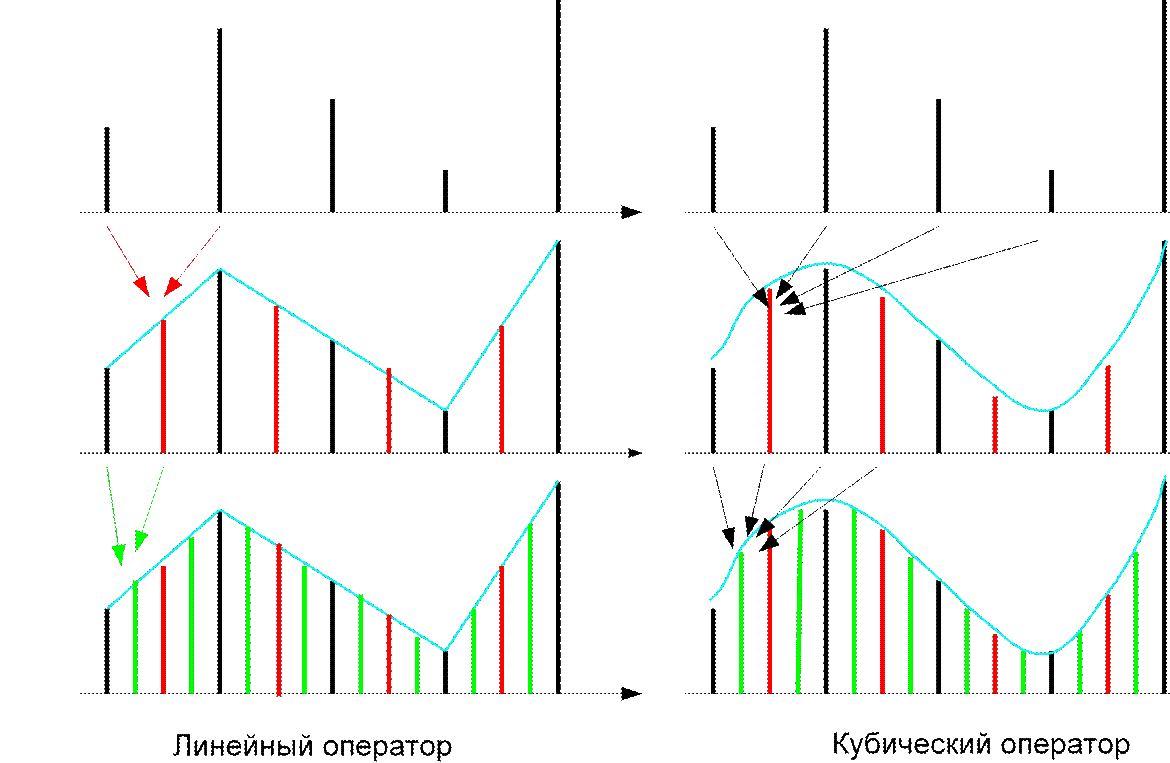
Этап обновления:

На этапе обновления коэффициенты             поднимаются при помощи  _j,k вейвлет-коэффициентов j,k

j,k :=j,kU j,k

Таким образом получим коэффициенты разложения в двух ветвях: H и G.

Обратное преобразование:

Вейвлет-базисы на основе интерполирующих функций

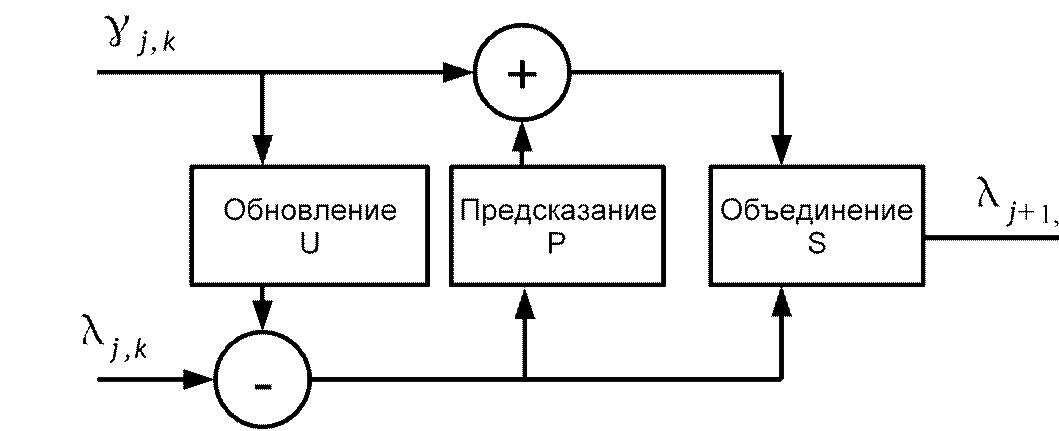
При рассмотрении системы анализа синтеза и лифтинговой схемы рассматривались методы полиномиальной интерполяции. При равноотстоящей дискретизации (с постоянной частотой дискретизации) возможно построение кардинального ряда:

N

st=∑ sn⋅xt−t_n.

n=0

В качестве примера кардинального ряда можно привести ряд В.А. Котельникова

xt=sin⋅t

при                    ⋅t

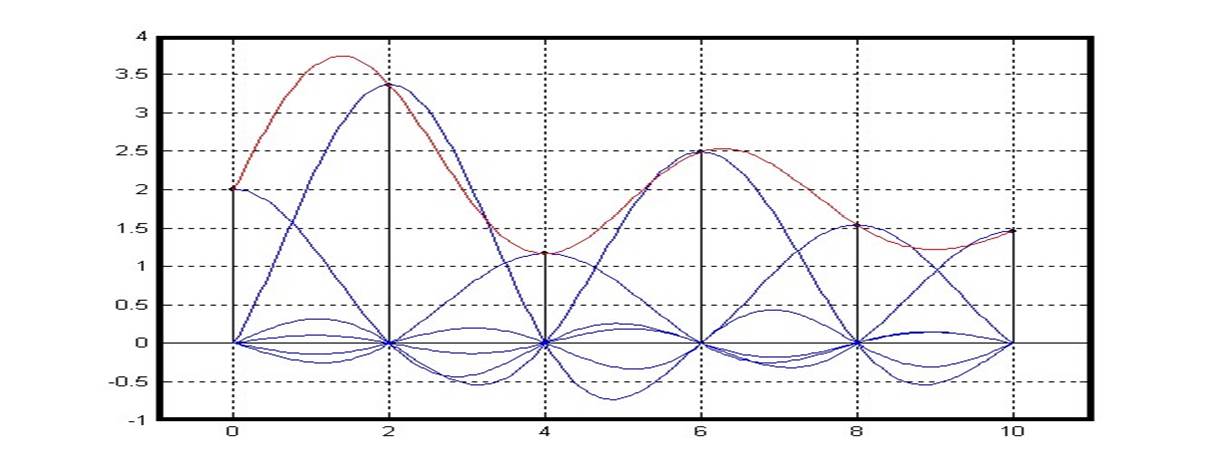
Продискретизируем кардинальный ряд с удвоенной частотой (для восстановления сигнала после децимации в системе анализа синтеза)

N

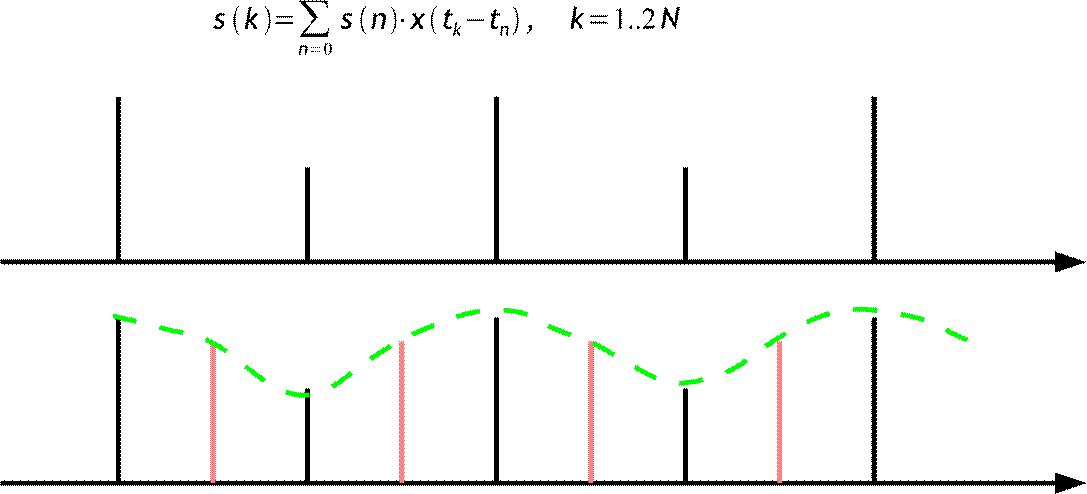
между отсчетами сигнала на выходе ветви разложения вставляются 0 а потом производится дискретная фильтрация сигнала при помощи фильтра с импульсной характеристикой xm

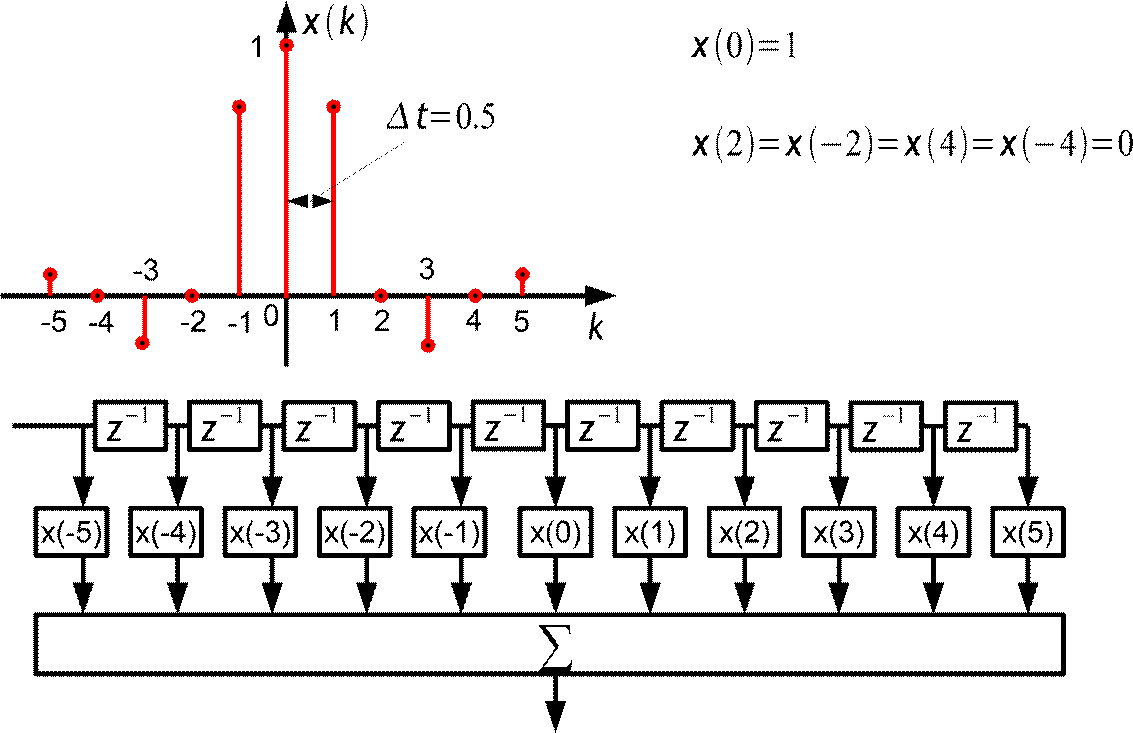
таким образом импульсная характеристика цифрового интерполирующего фильтра есть продискретизированная с шагом 0.5 интерполирующая функция.

В соответствии с теорией КМА, целочисленные сдвиги скейлинг-функции образуют ортонормированный базис в пространстве          . Это означает:V ₀

_n_,                                         n=0, n≠0;

−_∞                   n=1, n=0.

Таким образом, автокорреляционная функция скейлинг-функции

R_dt             является интерполирующей функцией.

Рассмотрим спектр продискретизированной с шагом 0,5 интерполирующей функции: x_dt=∑ xtt−nt,

n∈Z

X _d=∑ xntexp−jnt

n∈Z

_{поскольку все четные отсчеты, кроме нулевого равны 0, то} x2nt=n,

X _d=1∑ x2n1texp−j2n1t.

n∈Z

рассмотрим сумму

X _dX _d2=2∑ x2n1texp−j2n1t...

n∈Z

...∑ x2n1texp−j22n1t.

n∈Z

при t=0.5

X _dX _d2=2∑ x2n10,5exp−j2n1t...

n∈Z

... ∑ x2n10,5exp−j22n10,5;

n∈Z

тогда exp−j22n10,5=exp−j2n10,5exp−j2n1=−exp−j2n10,5

И в результате: X _dX _d2=2.

Вспомним свойство масштабирующего множителя уравнения КМА для скейлинг-функции ∣H ∣²∣H ∣²=1

Сравнивая с выражением    X _dX _d2=2                       получим

H₀= ^d X 2

2

коэффициенты масштабирующего уравнения рассчитаем через обратное преобразование Фурье



h₀=∫ H₀exp jntd

−

где h₀        соответствует коэффициентам со сдвигом 0,5. Для того чтобы выделить коэффициенты целочисленных сдвигов необходимо взять каждый второй отсчет hk=h₀2k

На практике наибольший интерес представляют симметричные вещественные интерполирующие функции, в результате скейлинг-функции также симметричные и вещественные. При этом их спектры – неотрицательные. Если спектр интерполирующей функции имеет отрицательные значения, то среди вещественных функций невозможно найти такую, чья АКФ является интерполирующей.

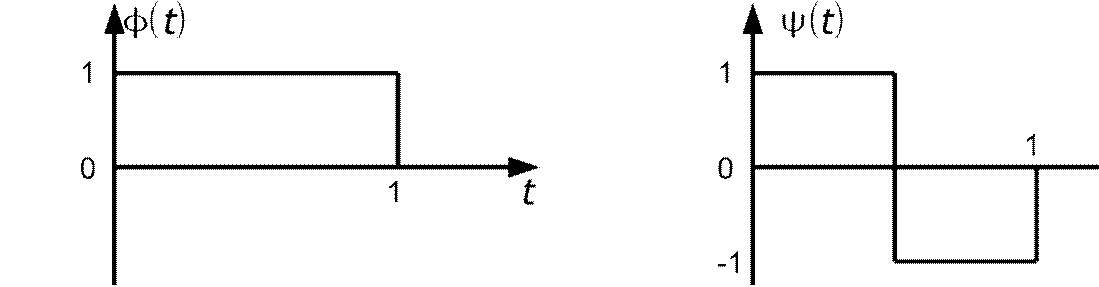
При использовании различных классов интерполирующих функций можно получать различные скейлинг-функции. В качестве примера можно произвести синтез базиса Хаара на основе сплайна первого порядка.

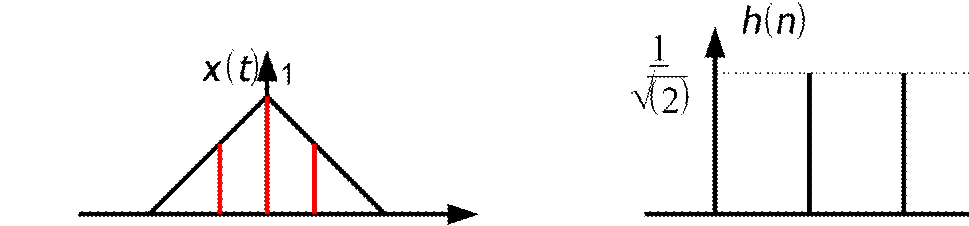
-1                0            1             t       0                             1          2 n

Рассмотрим функцию xt=sinct=sint t на ее основе получим скейлинг-функцию Шеннона t=sinct=sint t

Рассмотрим семейство xt= Pnt⋅sinct, Pnt=∑N an⋅t2n,a0=1, Pmt=∑M bn⋅t2m,b0=1, MN.

P mt                n=0                                      m=0

Частным случаем является функция            xtt

Меняя параметры полиномов числителя и знаменателя возможно изменять длительность интерполирующей функции  по времени и ее  эффективную ширину  спектра