Сжатие сигналов МТКС. Преобразования сигналов. Кодеры с Субполосные преобразованием кодеры, страница 2

C_ 0  d∞,

при этом

tdt=0.

Непрерывное изменение параметров а и b избыточно, поэтому вводят дискретные значения: a=a^m₀ ; b=n⋅b₀⋅a₀^m ; m,n∈Z , a₀1, b₀≠0.

C увеличением параметра масштаба увеличивается размер шага сдвига (при анализе на низких частотах детали не важны) . при b₀=1

_m,ntn

тогда по аналогии с рядом Фурье сигнал можно представить в виде набора дискретных коэффициентов разложения: ∞ d_m,n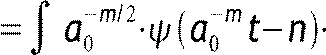stdt.

−∞

восстановленный сигнал в этом случае:

stn

m∈Z n∈Z

Основы теории кратномасштабного анализа

При КМА сигнал представляется в виде совокупности его последовательных приближений

Теория КМА базируется на теории функциональных пространств. Под КМА понимается описание пространства сигналов через вложенные не пересекающиеся подпространства:

...⊂V ₂⊂V ₁⊂V ₀⊂V₋₁⊂V₋₂⊂...

∩V _m=0,             ∪V _m=L₂R , m∈Z.

при этом если st∈V _m , _то   s2t∈V _m−₁ , а также существует базисная функция

₀ t∈V ₀ , и ее целочисленные сдвиги образуют ортонормированный базис  V ₀ ,

при этом функции m,nt=2−m/2 2−m x−n, образуют ортонормированный базис V m сигнал может быть представлен посредством последовательных приближений в V _m st= lim s_mt,

m−∞

тогда появляется возможность анализа  сигнала на различных уровнях разрешения или масштаба. При этом базисная функция удовлетворяет первому основному уравнению КМА:

t.                                                           _(!)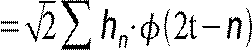

n

масштабирующая (scaling) функция и параметры           тесно связаны между собой: h_n

m1,kt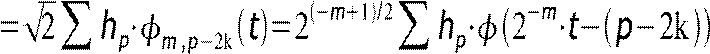. p p

При этом выражение (!) можно представить в частотной области:

,

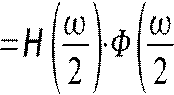_где                           H =∑h_n⋅exp−j⋅⋅n  масштабирующий множитель уравнения КМА

n

При  рекурсивном применении  масштабирующего уравнения КМА:

∞

     .

m=1    2

Свойства коэффициентов масштабирующего уравнения для скейлинг-функции:

Свойство 1. . n

Свойство 2.                                2⋅∑hn⋅hn2k=k.

n

Свойство 3. ∣H ∣²∣H ∣²=1

Введем понятие подпространства           как ортогональное дополнение W _m пространства                    доV _m   V _m−1

V _m−1=V _m∗W _m ,       ∩W _m=0, ∪W _m=L²R .

пусть t    образует ортонормированный базис пространства         , тогда W 0

t∈W 0⊂V −1           и можно представить как разложение по базису V −1

t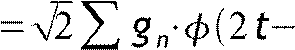n                             _(!!)

n

Выражение (!!) представляет собой масштабирующее уравнение для вейвлет-функции по аналогии со скейлинг-функциями определим семейство вейвлет-функций m,nt=2−m/2 2−m t−n.

Тогда масштабирующее уравнение для вейвлет-функции в частотной области имеет вид

,         =G^.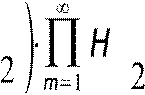

Свойства вейвлет-функции:

Свойство 1.	∑hn⋅gn=0 ⇒ gn=−1 h−n1 n
Свойство 2. Свойство 3.	G=−H −⋅exp−j⋅ 0=0, ⇒ ∑gn=0;

n

n

В этом случае сигнал можно представить в виде проекции на           (грубой V _m аппроксимации) и множества деталей как проекцию на W _j

st=∑cm,n⋅m,nt∑d j,k⋅j,kt

n                           j

В качестве примера вейвлет-базиса можно рассмотреть вейвлет Хаара:

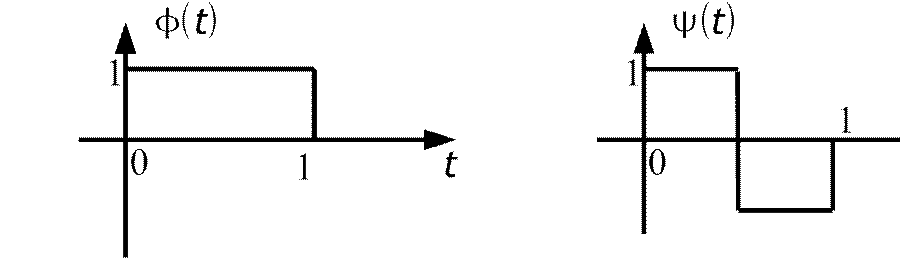
                                                                   h=[ ^{1      1} ];                      g=[ ¹  − ¹ ];

2 2                  2 2

Дискретное вейвлет-преобразование (ДВП, DWT)

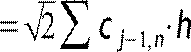Как было показано выше, базисные функции основных уравнений КМА зависят от коэффициентов уравнений КМА h и g. Т.о, возможно построение  базисных функций на основе коэффициентов уравнений КМА h и g, а также возможно производить анализ дискретных сигналов без использования базисных функций, путем итеративного вычисления коэффициентов разложения, получив таким образом полностью дискретный процесс декомпозиции:

c j,kn2k ;

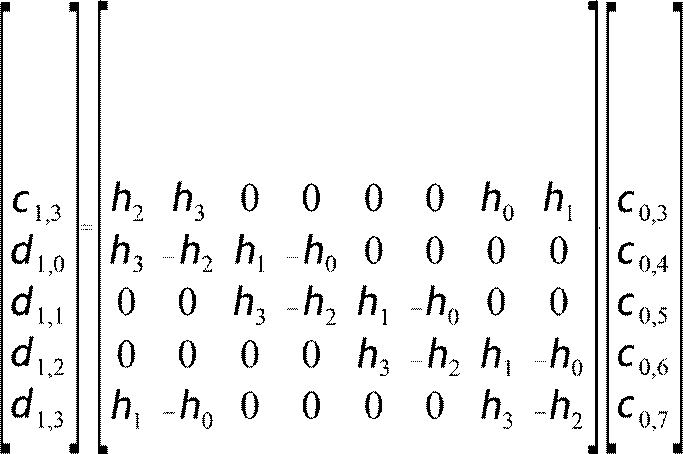n

dj,k=2∑c j−1,n⋅gn2k .

Матричное описание:      ⁿ c1,0        h0 h1 h2 h3    0    0    0    0     c 0,0 c1,1 0    0 h0 h1 h2 h3        0    0    c0,1  v j1=M j⋅v j; c1,2          0    0    0    0 h0 h1 h2 h3 c0,2

v jv j1;

представление посредством системы банк-фильтров (субполосного кодирования)

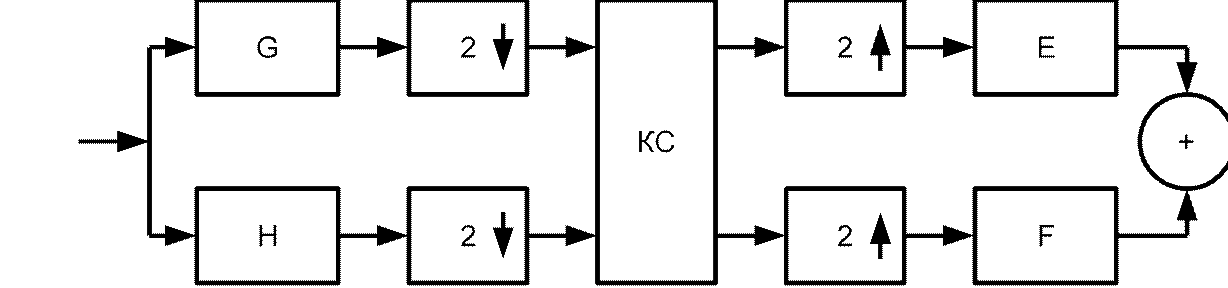
сигнал делится на 2 ветви: НЧ (H – ветвь), которая выделяет информацию и ВЧ (G – ветвь), определяющую детали. Применяя рекурсивно к H – ветви получим:

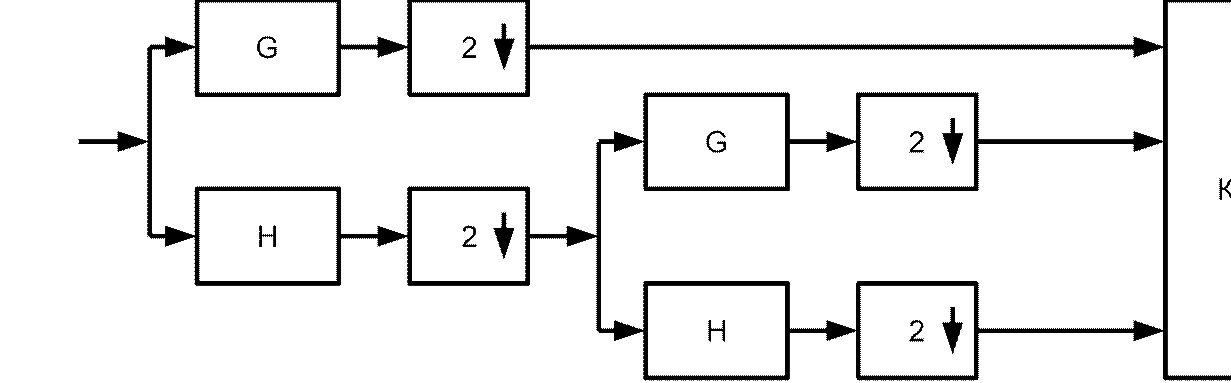
Заменим эквивалентной структурой системы анализа

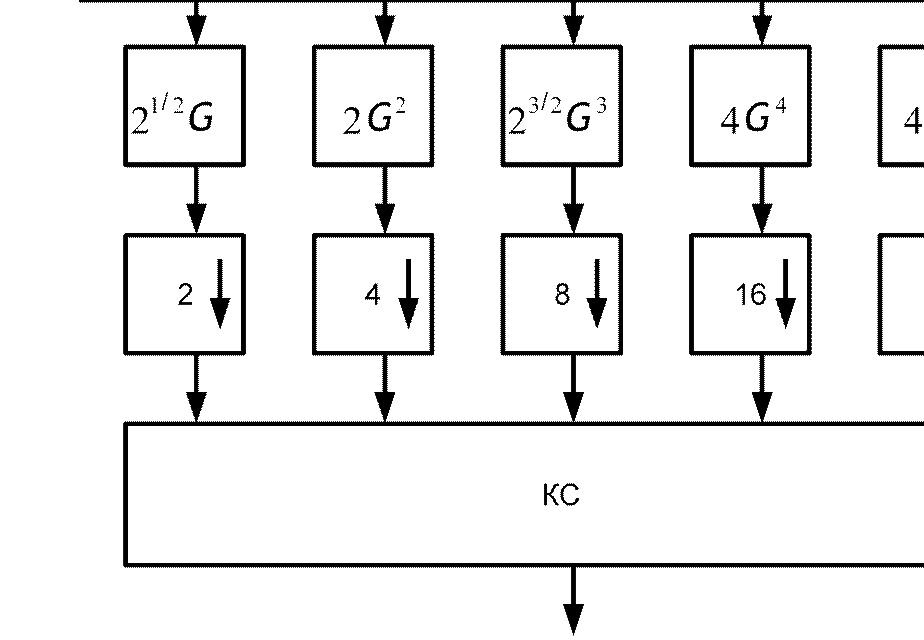
Условие полного восстановления сигналов

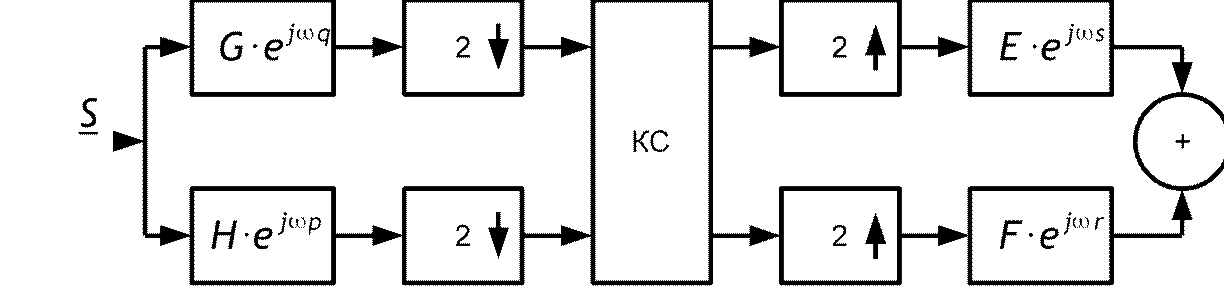
O =[F H exp jprE G exp jqs]S ...