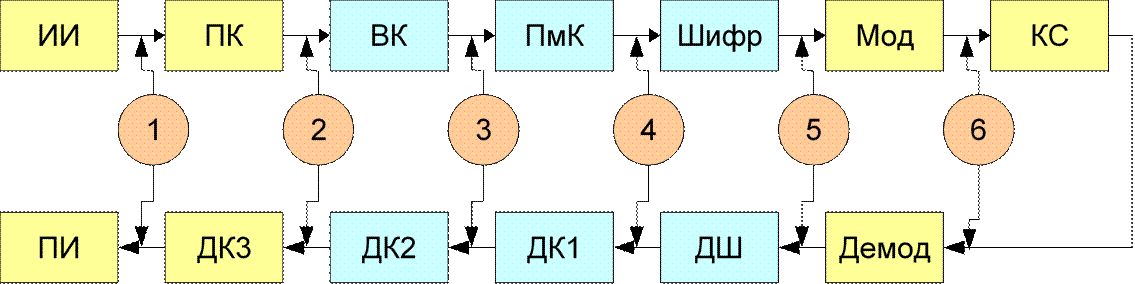
Основные блоки
ИИ – источник информации
ПК – первичный кодер
ВК – вторичный кодер
ПмК – помехоустойчивый кодер
Шифр – шифратор
Мод – модулятор
КС – канал связи
Демод – демодулятор
ДШ – дешифратор
ДК – декодер
ПИ – получатель информации
1 – исходная информация
2 – битовый поток
3 – сжатый битовый поток 4 – внесение избыточности для исправления ошибок передачи 5 – шифрование 6 – модулированный сигнал на выходе
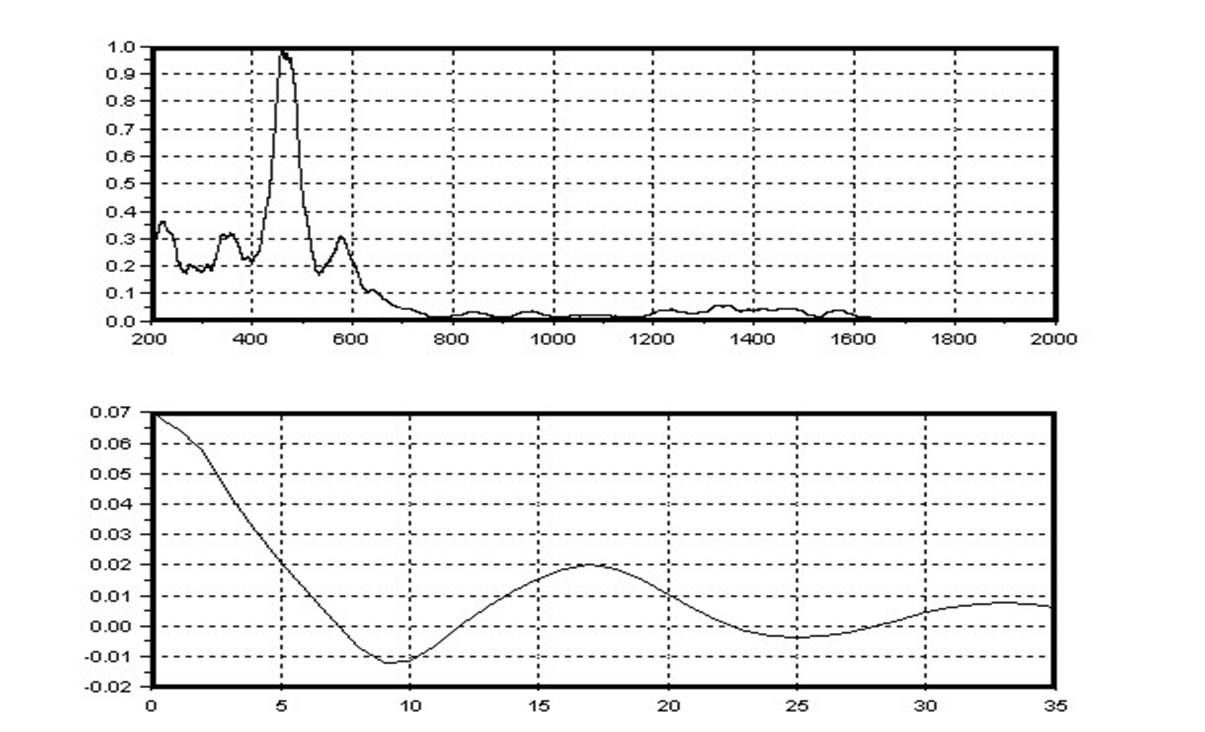
Пример речевого сигнала (РС) и Основные свойства сигналов его спектра МТКС:
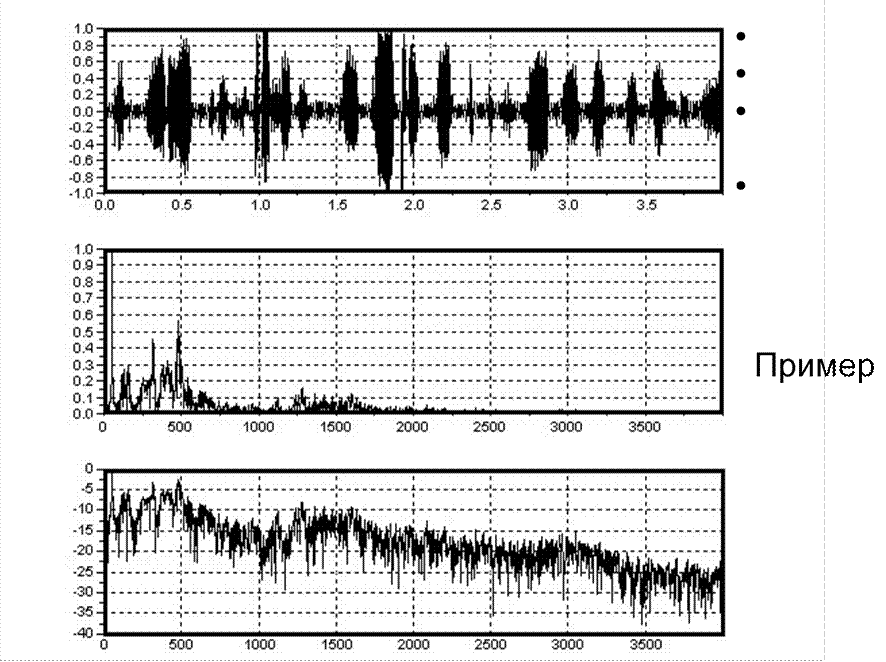 Нестационарность
Нестационарность
Изменчивость во времени
Широкий динамический диапазон изменения
Сложность математического описания
РС построен для фразы длительностью 4 с. при частоте дискретизации 8 кГц.
Статистическая модель РС
xt - непрерывный случайный процесс (СП), который описывает РС
Корреляционная функция СП
Rx=E [xt⋅xt−]
Спектральная плотность мощности (СПМ) СП
S
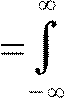 Rx⋅exp− j⋅⋅d
Rx⋅exp− j⋅⋅d
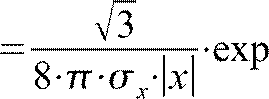
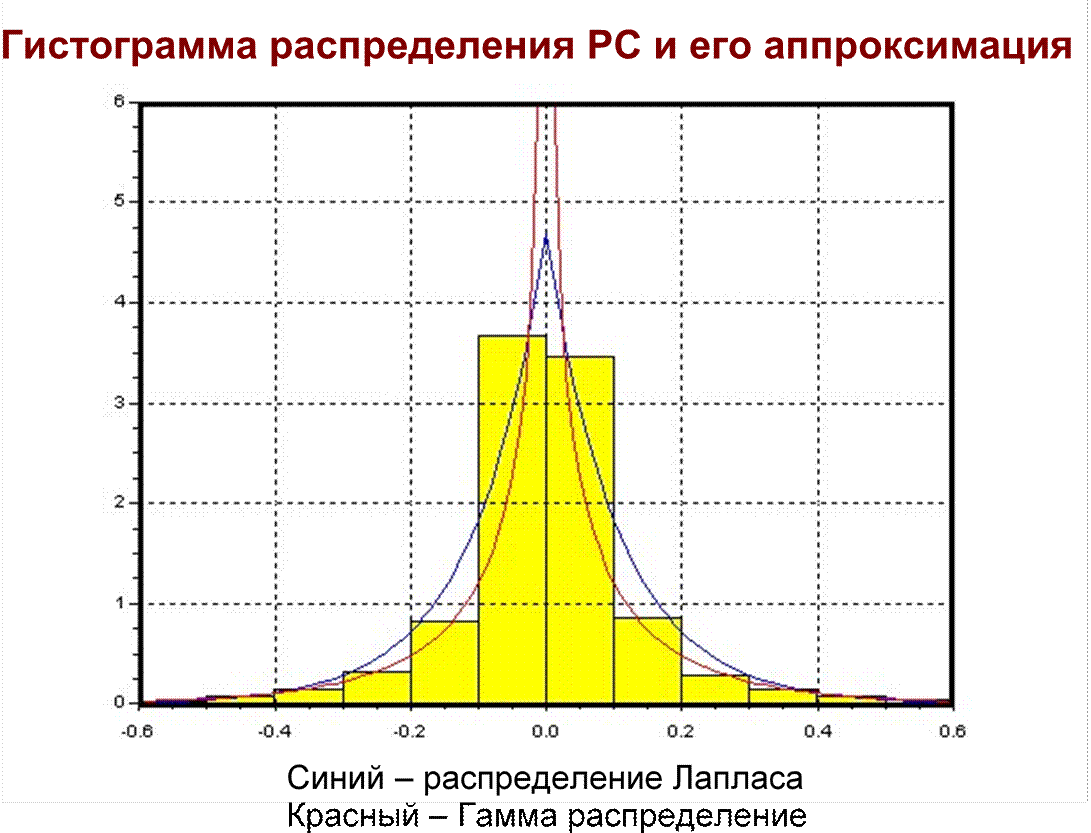
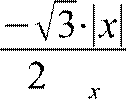 Аппроксимация ФПВ РС при помощи гамма-распределения px
Аппроксимация ФПВ РС при помощи гамма-распределения px
⋅
Аппроксимация
ФПВ РС при помощи распределения Лапласа px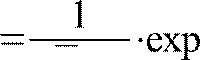
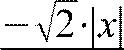
2⋅x x
Первичное кодирование РС
Дискретизация сигналов с ограниченным спектром
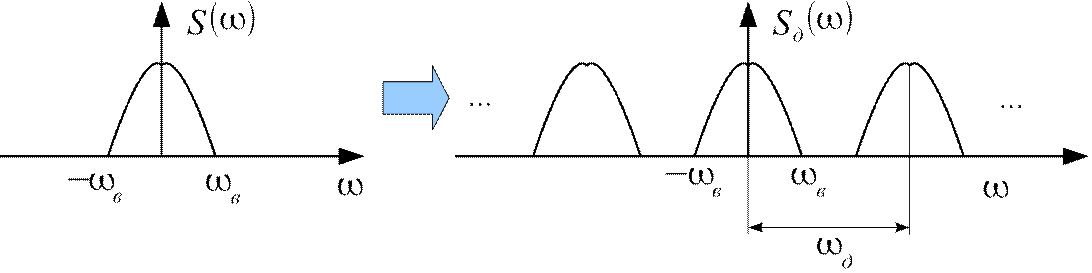
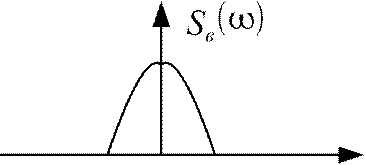
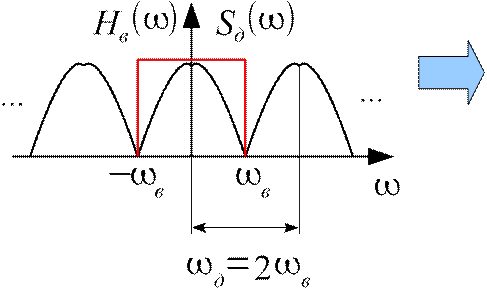 −в в
−в в
Дискретизация сигналов.
Если д2⋅ в , тогда периодические спектральные составляющие не перекрываются и исходный сигнал может быть получен при помощи идеального ФНЧ, при этом во временной области справедлив ряд В.А. Котельникова:
∞
st=∑ sn⋅t⋅sinс2⋅⋅t−n⋅t,
n=0 t
где sinсt=sintt , t=2⋅д - интервал дискретизации
Графическое представление ряда В.А. Котельникова
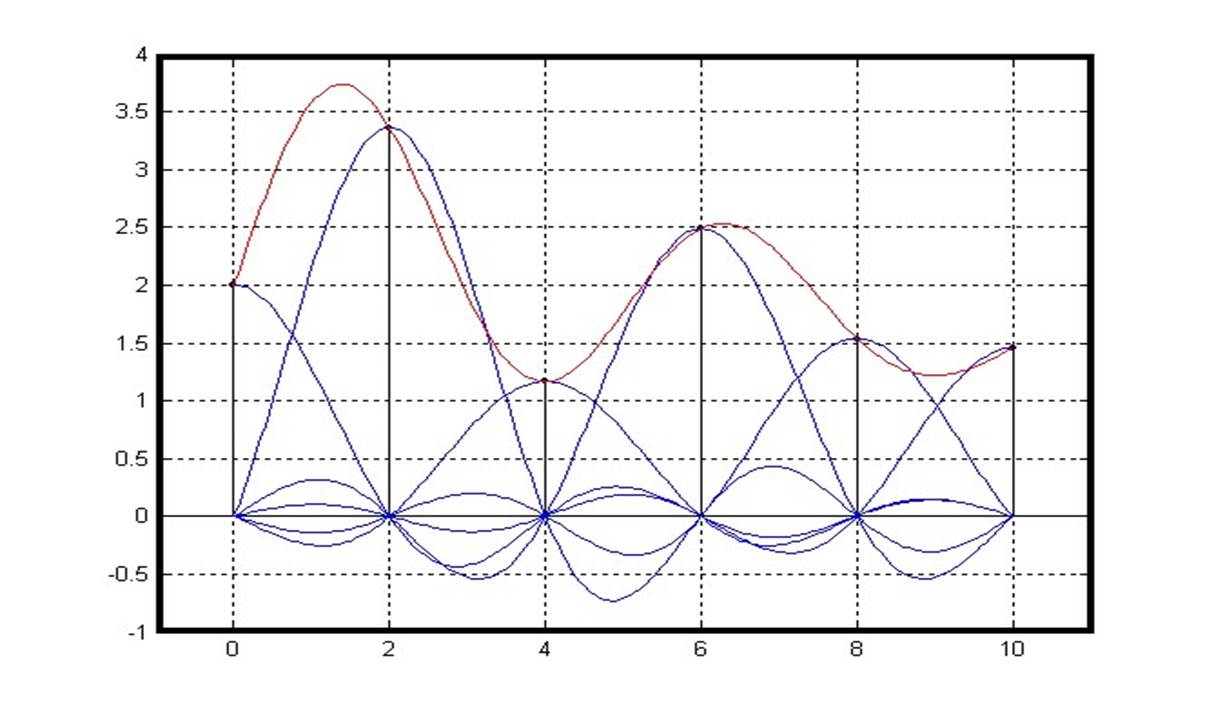
Выбор частоты дискретизации
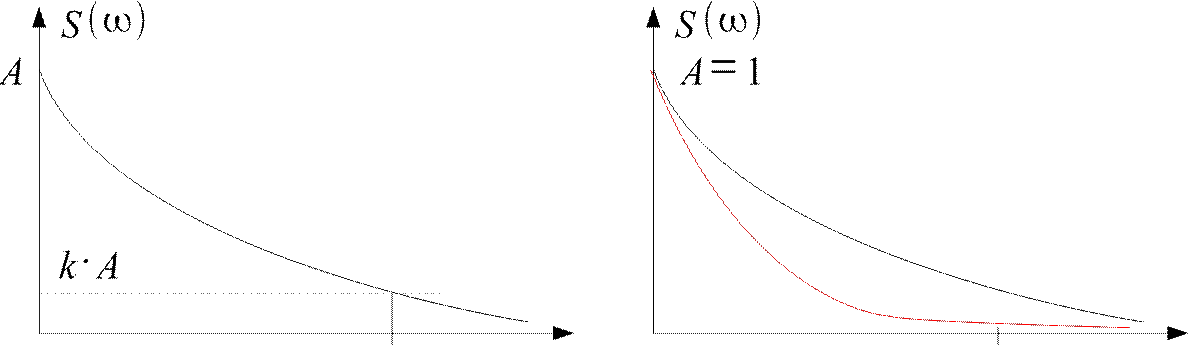
в в
1. Амплитудный метод оценки. 2. Энергетический метод оценки в
Sв=k⋅A 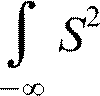 d
d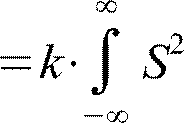 d
d
k=0.9, 0.95, 0.99
Для РС верхняя частота по уровню -30 дБ составляет 4кГц
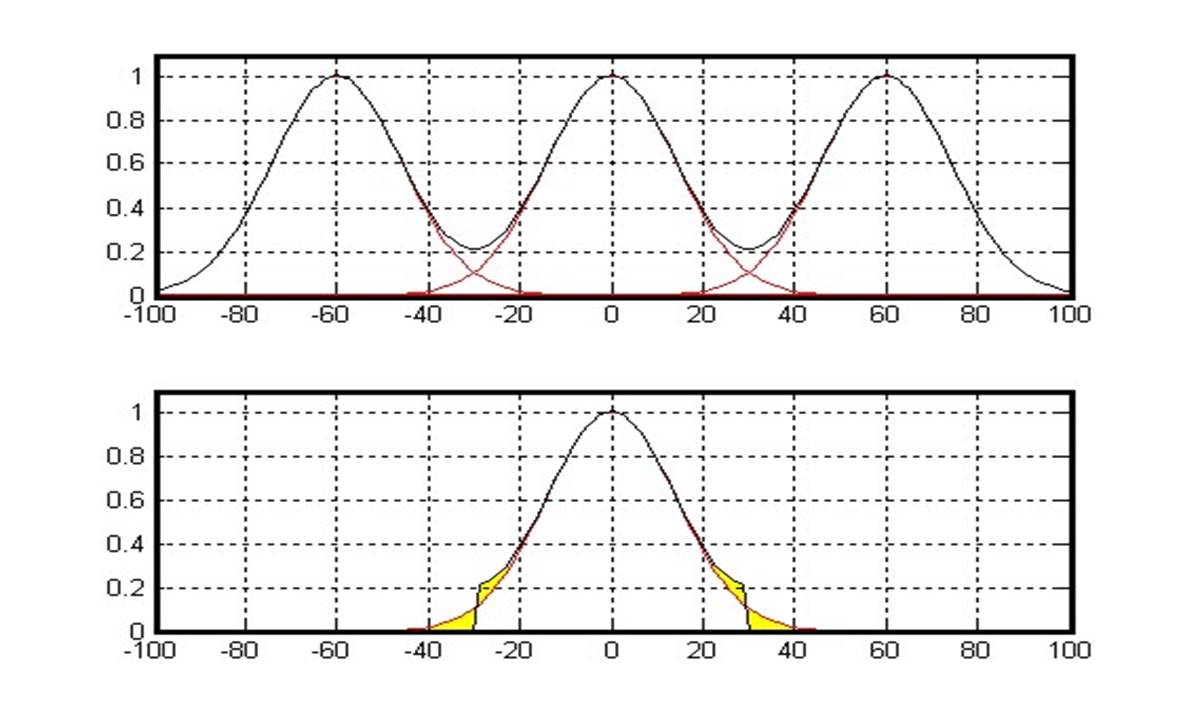
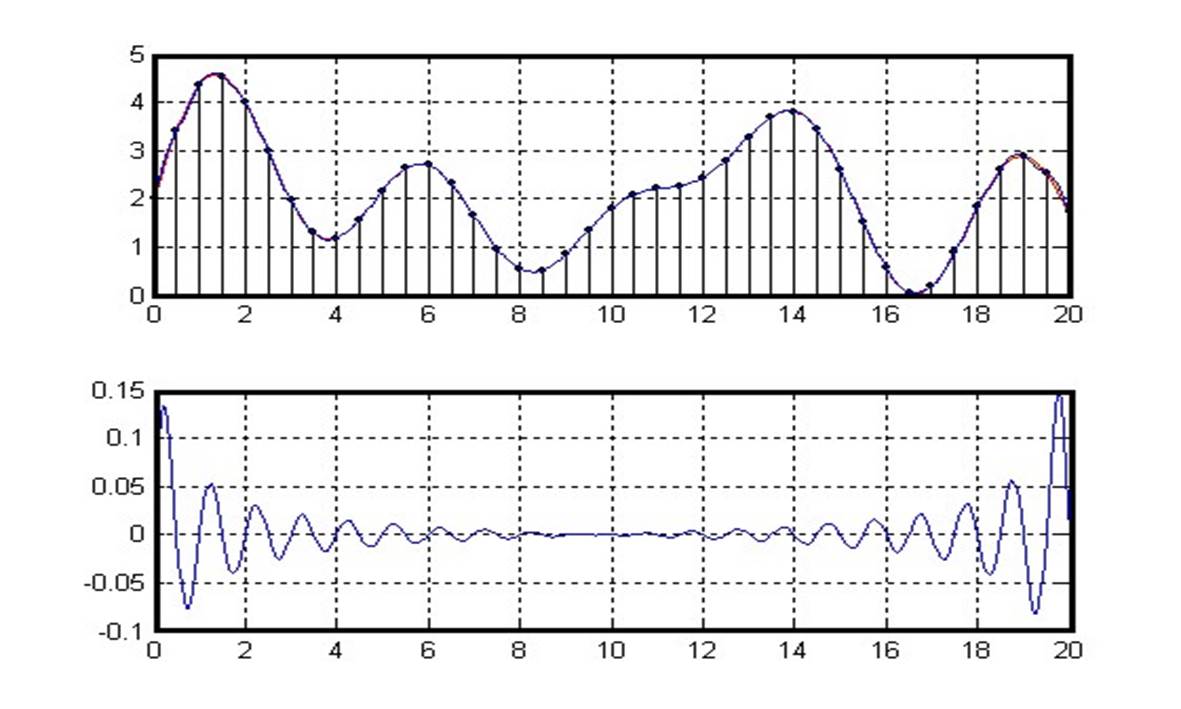
Метод борьбы с ошибками наложения:
1. Использование ограничивающих ФНЧ (антиэлайзинговых фильтров)
2. Использование ФНЧ компенсирующих ошибки наложения при восстановлении
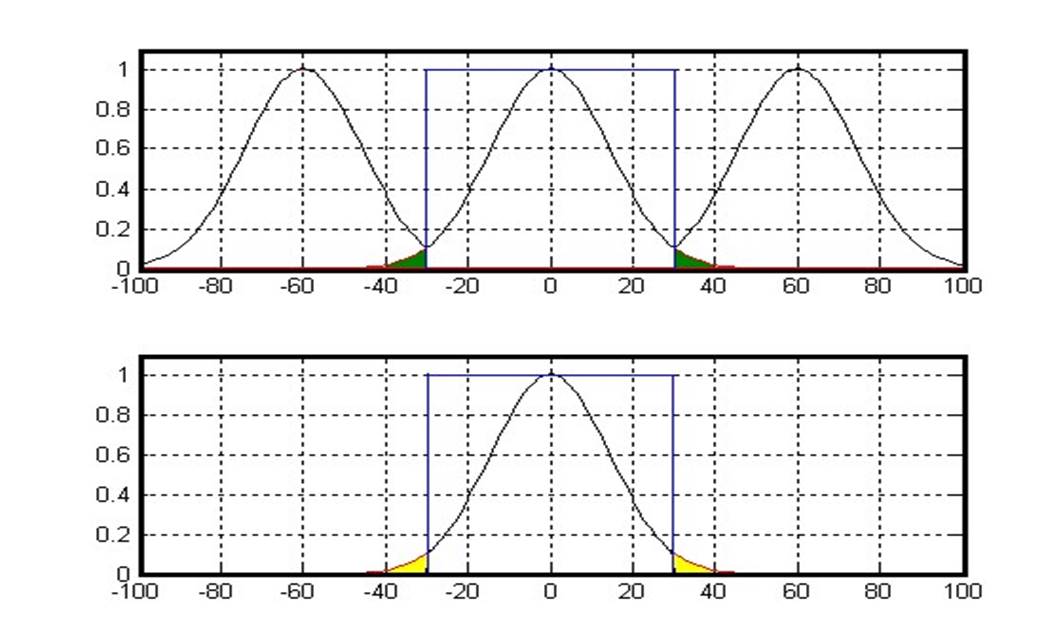
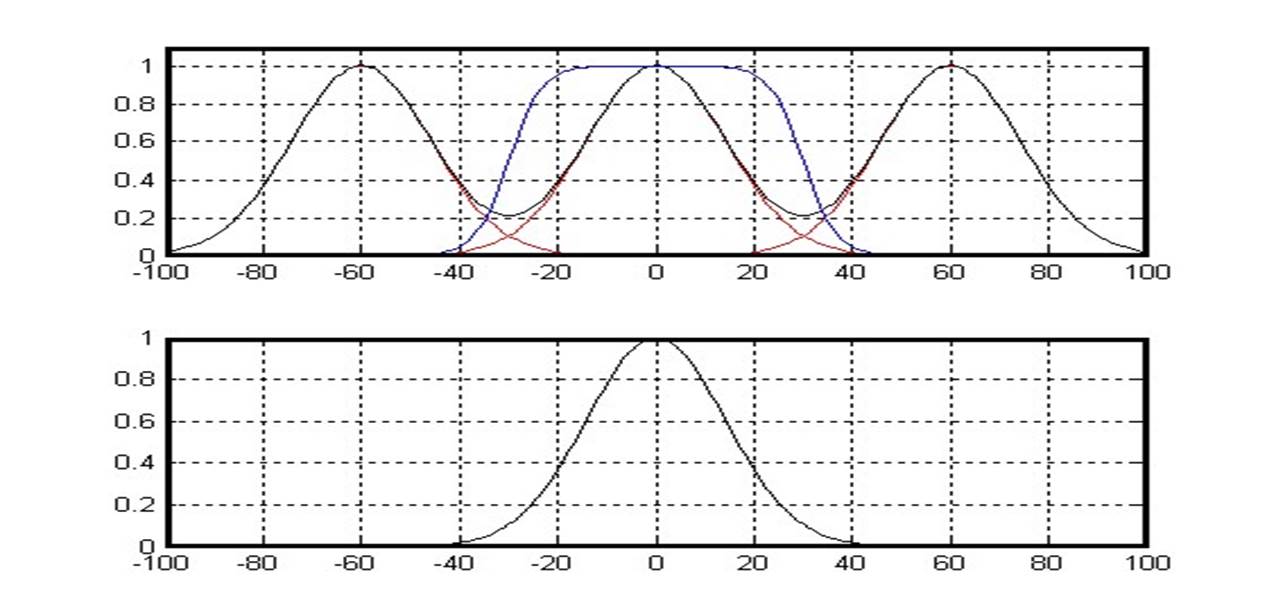
H
= ![]() S 2 АЧХ
восстанавливающего фильтра Sд⋅
S 2 АЧХ
восстанавливающего фильтра Sд⋅
⋅2 - стабилизатор, =10−5...10−9
Метод борьбы с ошибками усечения:
1. Увеличение интервала обработки
2. Использование специальных восстанавливающих функций
xt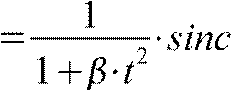 t
t
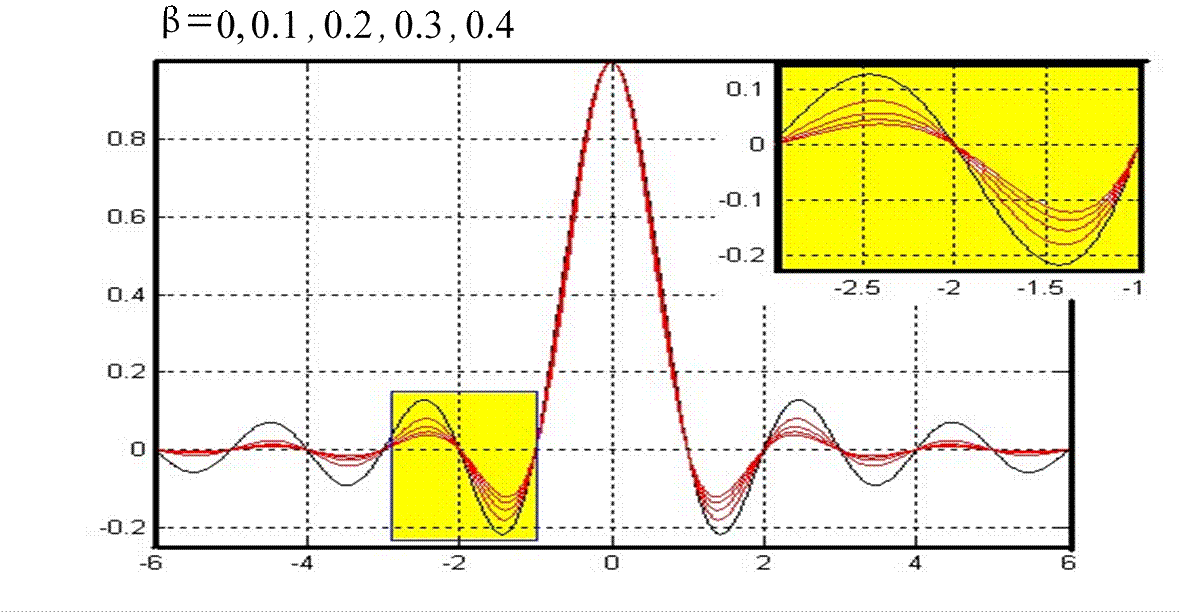
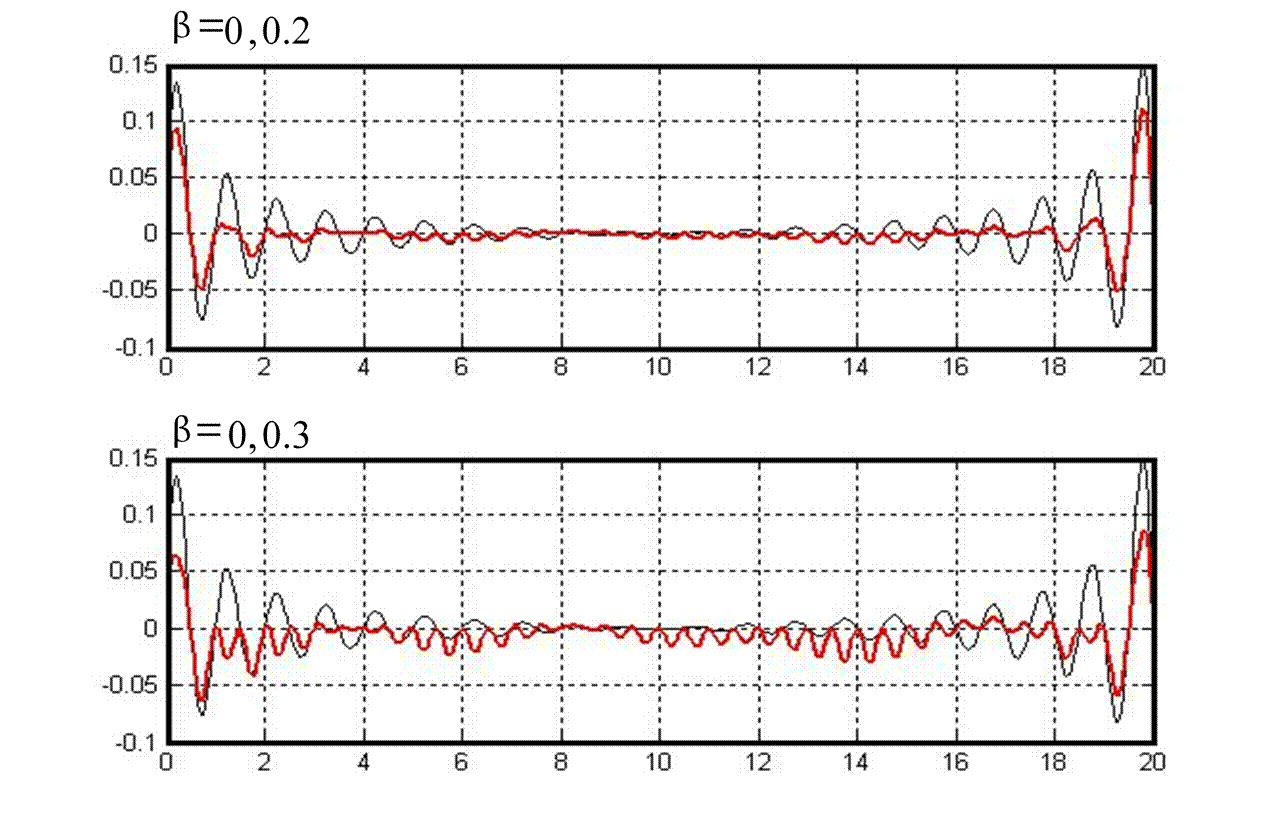
Квантование РС в МТКС
xn 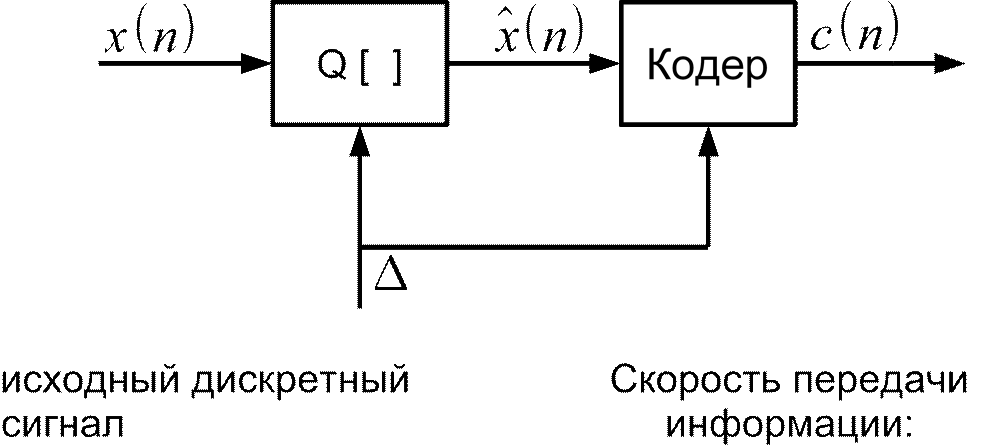
Q [ ] квантователь с=B⋅F д бит/c
xn цифровой сигнал для уменьшения скорости передачи информации необходимо снизить
шаг квантования количество бит на отсчет c n битовый поток
Пусть отсчеты сигнала попадают в конечный интервал значений при котором
тогда при использовании аппроксимации ФПВ РС распределением Лапласа можно считать:
−4⋅xxn−4⋅x ,
Вне интервала окажется менее 0,4% отсчетов РС.[−4⋅ x ,4⋅x ]
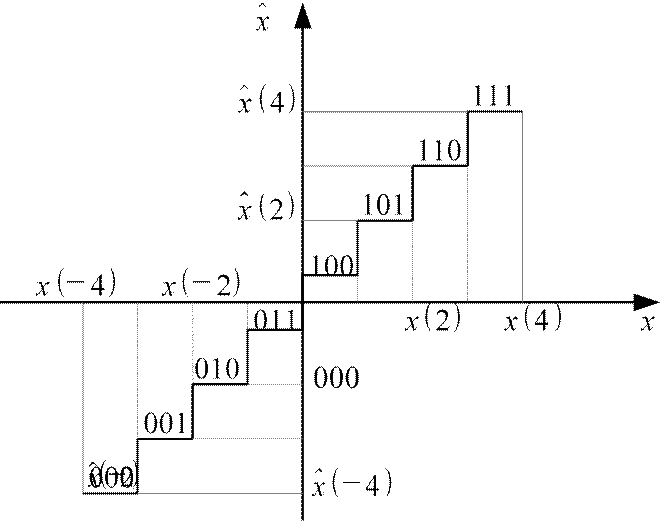 если значение
x(n)
если значение
x(n)
попадает между x(1) и x(2), то на выходе будет кодовое слово 101.
xi−xi−1= и x i−x i−1=
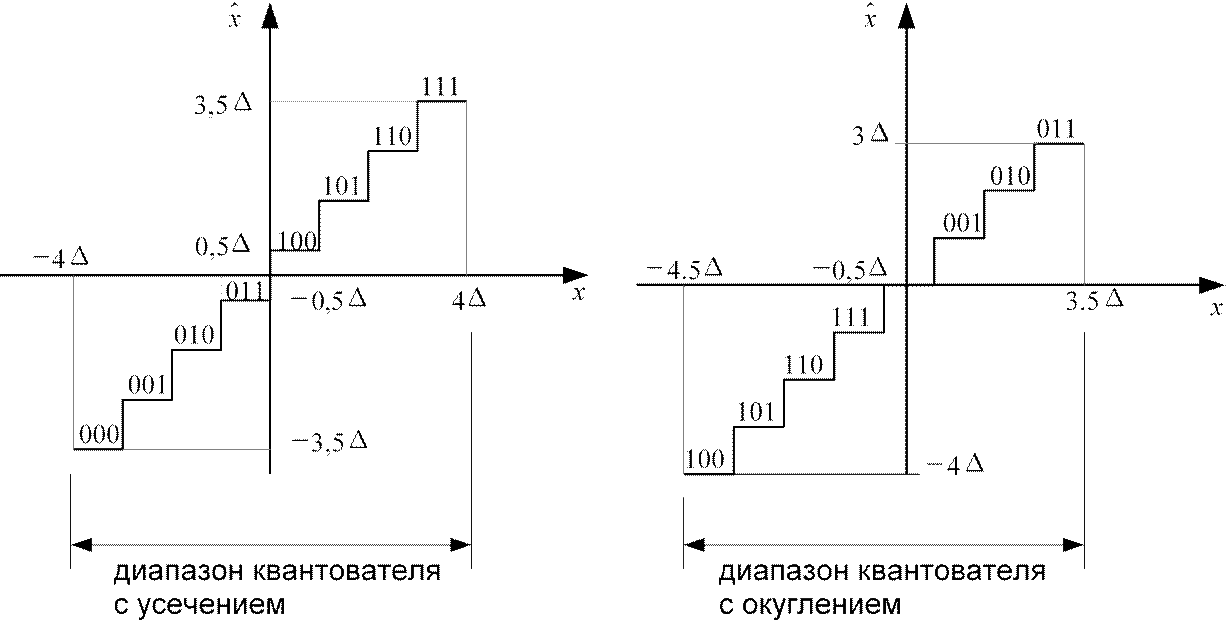
Квантователь с усечением:
x n=/2signcncn,
где signcn=1, ecли c1=0 signcn=−1, ecли c1=1
Квантователь с округлением:
x n=cn.
Для равномерных квантователей необходимо задать число уровней квантования и шаг квантования. Число уровней квантования выбирается равным 2B если ∣xn∣Xmax , то
2⋅X max=⋅2B .
=2Xmax/2B - Шаг квантования
Сигнал после квантования: x n=xnen,
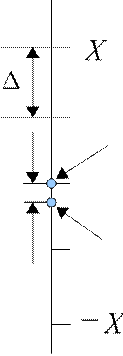 max
max
x n −/2en/2
en2 2 - дисперсия шума квантования при равномерном
xn e 12 распределении ошибки
max Оценка отношения сигнал-шум квантования имеет вид:
S X
![]()
![]() q 2=10⋅lg 22⋅12=10⋅lg
22B⋅12=20⋅B⋅lg2−10⋅lg
16 дБ
,
q 2=10⋅lg 22⋅12=10⋅lg
22B⋅12=20⋅B⋅lg2−10⋅lg
16 дБ
,
⋅16 4⋅16
X2
где S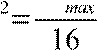 - дисперсия исходного
сигнала
- дисперсия исходного
сигнала
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.