Обобщенная структурная схема системы передачи информации. Сигналы МТКС и их свойства, страница 3

Рассмотренные выше вопросы неравномерного квантования позволяют согласовать широкий диапазон изменения РС и ограниченное количество уровней квантования. Альтернативный метод заключается в адаптации свойств РС. 

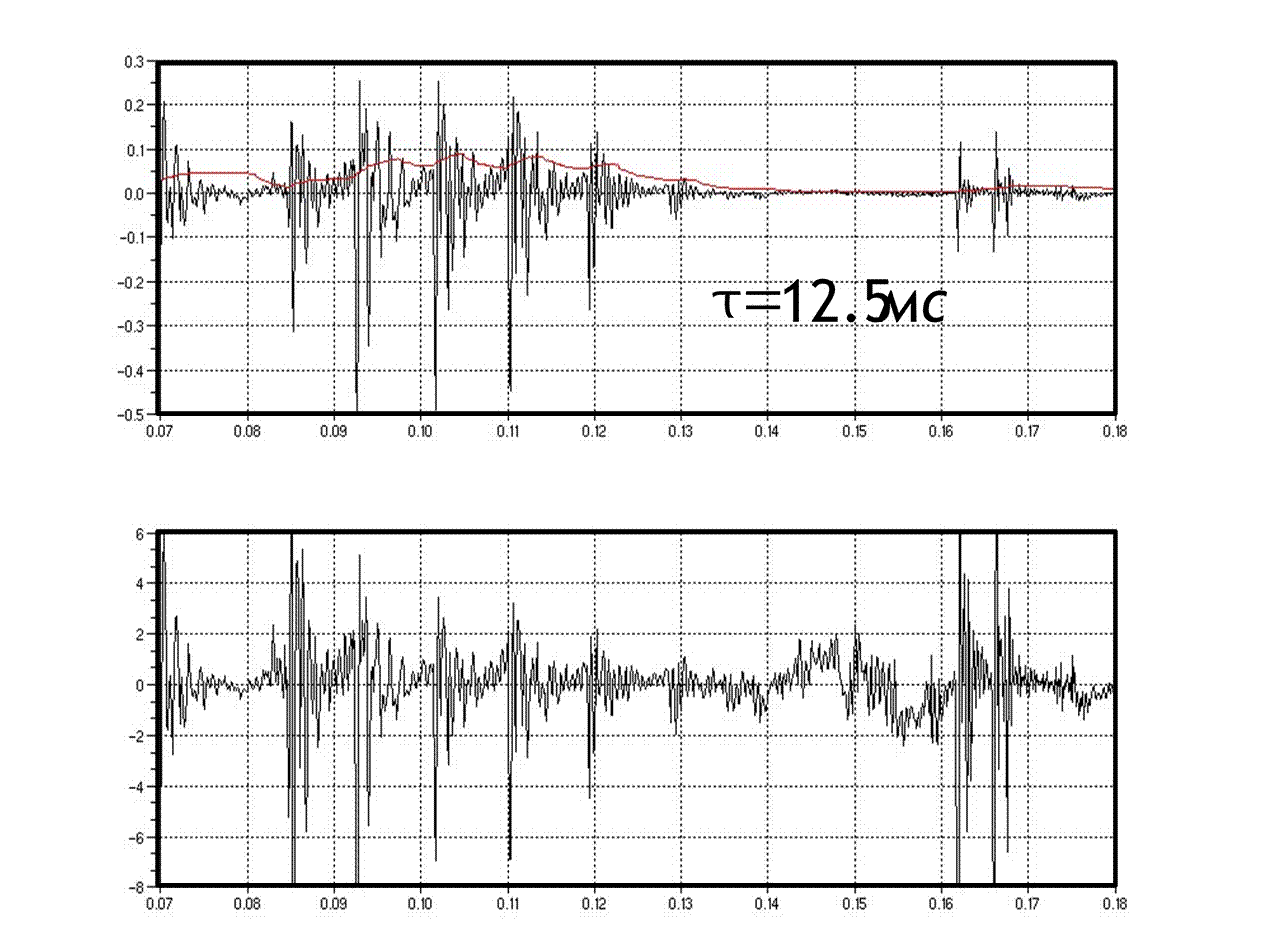
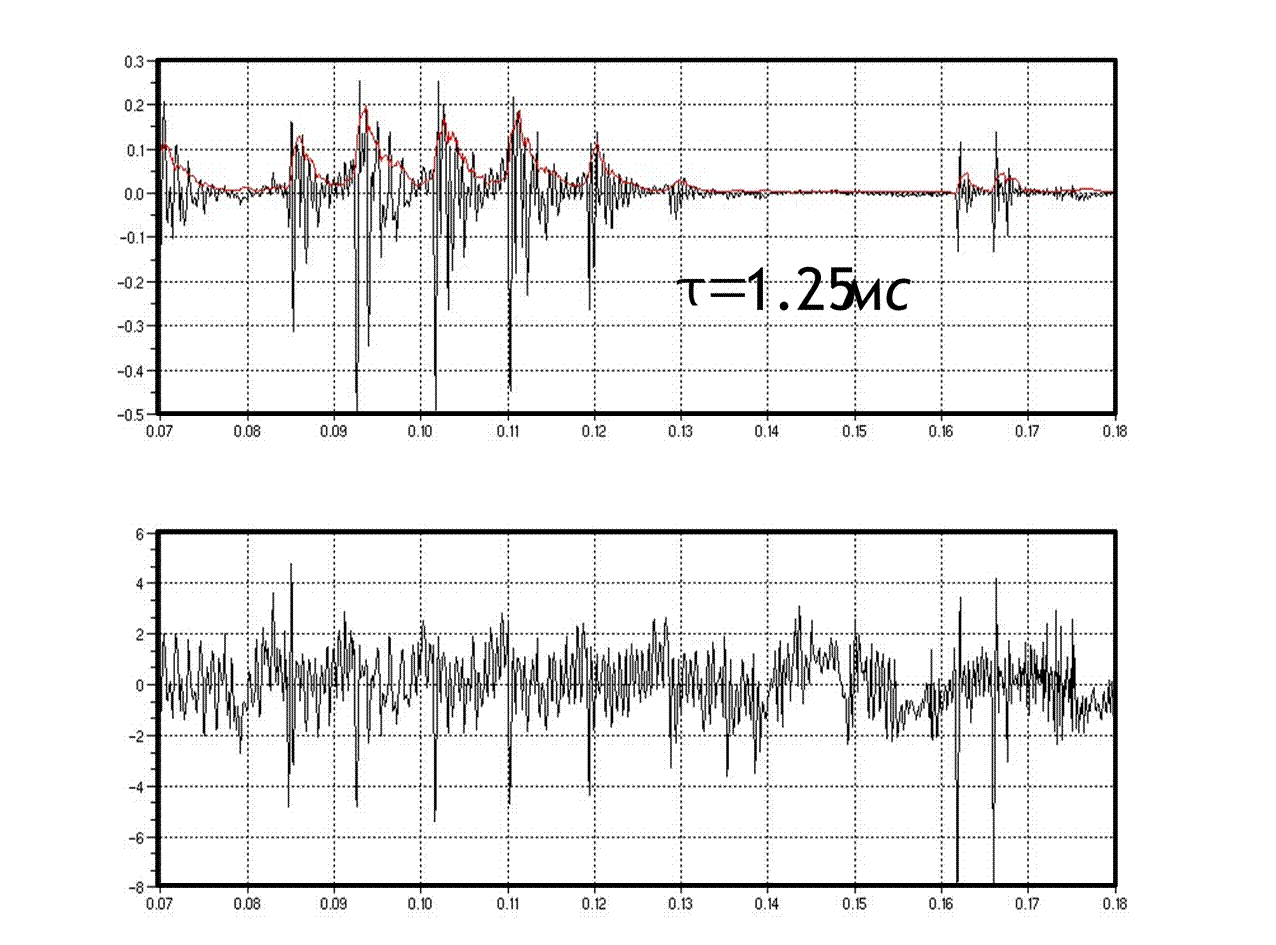
Амплитуда РС  может меняться в широких пределах при переходе от вокализованного к невокализованному сегменту.

Адаптация по входном сигналу

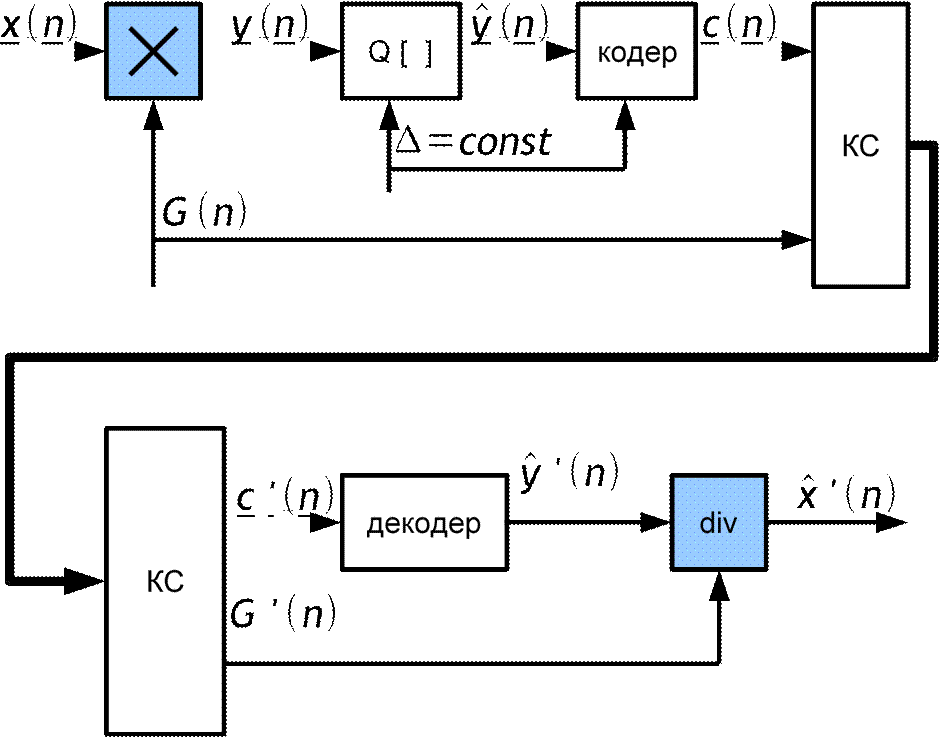
Структурная схема квантователя с адаптацией по шагу

Структурная схема квантователя с адаптацией по коэффициенту усиления

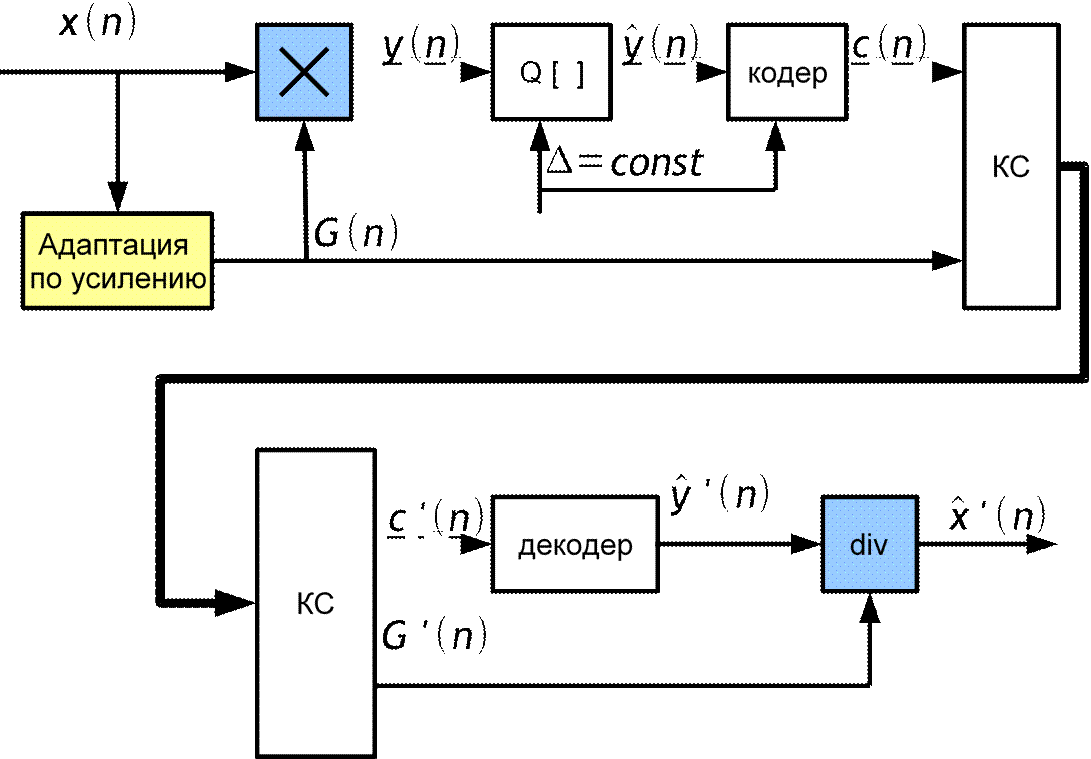
Для адаптации используют ФНЧ, на выходе которого сигнал определяет кратковременную энергию РС

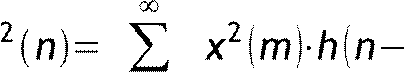m,

m=−∞

h n =ⁿ⁻¹ , n1 ; h n =0, в противном случае

n=₀⋅n ;

G⁰

Gn=n ;

Адаптация по выходном сигналу

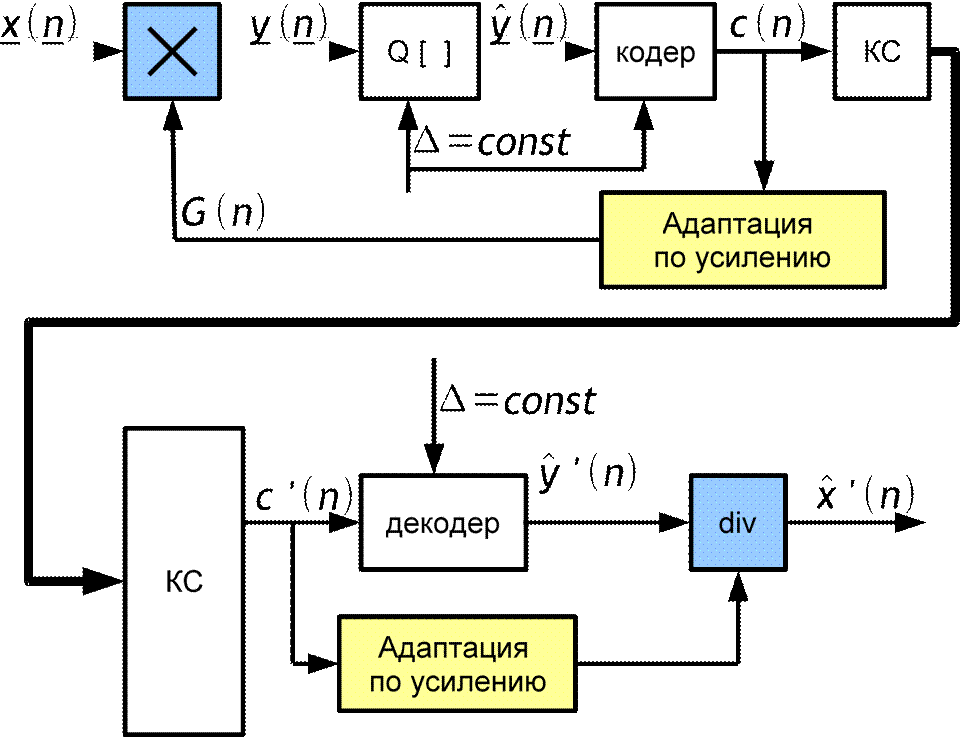
Структурная схема квантователя с адаптацией по усилению 

Структурная схема квантователя с адаптацией по шагу

m=−∞

h n =ⁿ⁻¹ , n1 ;          h n =1/M , 1nM ;

h n =0, в противном случае     h n =0, в противном случае

n=₀⋅n ;

G⁰

Gn=n ;

Разностное кодирование РС

Анализ корреляционной функции РС позволяет сделать вывод о том, что РС медленно меняется на от отсчета к отсчету. Поэтому целесообразно кантовать не сам РС а разность между соседними отсчетами.

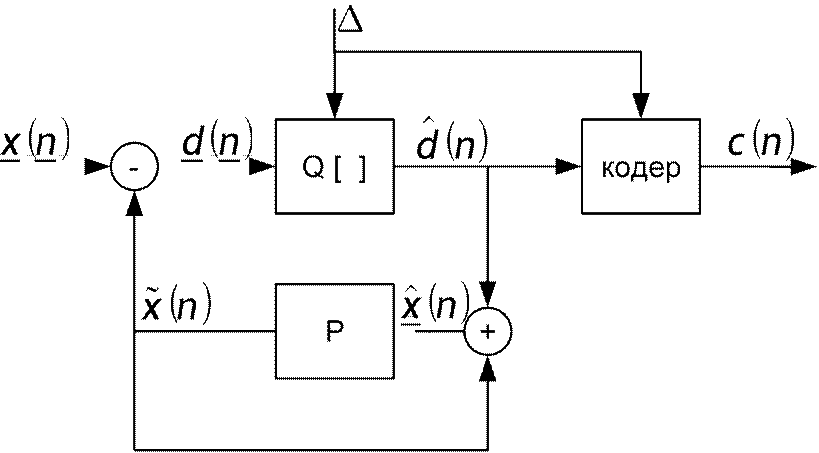
d n=x n− x n;  x n=x nd n;  d n=d ne n; d n=x n− x nd n−e n ;  x n− x n =e n ;

                                                                                                                                         q=  = =G _P⋅q₀

e        d

^d2

q0= ₂      - отношение сигнал-шум квантования _e

GP=^22x - коэффициент усиления вызванный разностным кодированием _d

Для увеличения отношения сигнал-шум необходимо увеличить коэффициент усиления, т.е. уменьшить ошибку предсказания. 

P

x n=∑ _k⋅x n−k ,

k=1

Предсказанное значение – выходной сигнал фильтра с передаточной характеристикой

P

P z=∑ _k⋅z^−k ,

k=1

Восстановленный сигнал – выходной сигнал фильтра с передаточной характеристикой

1

H z=                     _P      ,

1−∑ _k⋅z^−k

k=1

E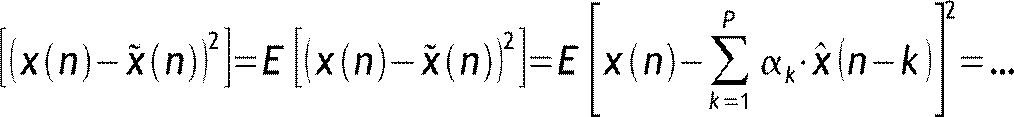

...=E .

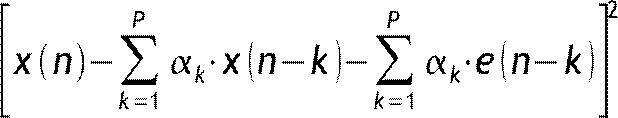Для минимизации ошибки квантования необходимо продифференцировать (***) и приравнять к нулю.

^P

xn−^∑ _k⋅[x n−k en−k ]⋅xn− jen−j]=0.                 ^(!)

k=1

С учетом (*)

E [xn−x n−k⋅x n−j]=E [dn⋅x n−j]=0. если дисперсия ошибки предсказания мала, то ошибка предсказания не коррелирована с сигналом на входе предсказания,                и тогда раскроем математическое x n−j

ожидание в уравнении (!):                                                            _P

E [xn− jxn]E [en−jxn]=∑ _k⋅E [xn−kxn−j]...

k=1

P                                                            P

...∑ _k⋅E [xn−ken− j]∑ _k⋅E [en−kxn− j]...

k=1                                                       k=1

P

...∑ _k⋅E [en−ken−j].                                                         _(!!)

k=1

E [xn− jxn]=R _x j; автокорреляционная функция

E [en− jxn]=0;     не коррелированы

E [xn−kxn− j]=R x j−k; автокорреляционная функция

E [xn−ken− j]=0; не коррелированы

E [en−kxn− j]=0; не коррелированы

E [en−kenk; автокорреляционная функция белого шума тогда (!!) примет вид:

P

R _x j=∑ _k⋅[R _x j−k;                                                 (!!!)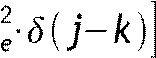

k=1

Введем нормированную АКФ

x j=R x2j, тогда               x j k=1 ke2⋅ −  ;

x