Обобщенная структурная схема системы передачи информации. Сигналы МТКС и их свойства, страница 4

или в матричной форме         _x=С , где

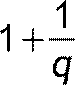                                                                 1   ⋯ P−1

С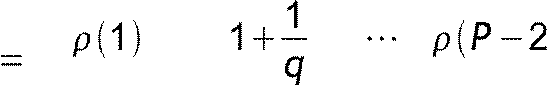〛 =С−1x.

⋮

P−1 P

Для расчета коэффициентов линейного предсказания необходимо знать отношение сигнал-шум ошибки предсказания. Предположим что отношение сигнал шум велико, тогда

.

Кодеки речи. Дельта – модуляция. Линейная дельта - модуляция

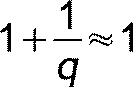Уменьшение интервала дискретизации приводит к увеличению корреляционных связей  между отсчетами РС. При этом использование одноразрядного квантователя может дать хорошие результаты. Скорость передачи в этом случае равна частоте дискретизации.

Частота дискретизации много больше частоты Котельникова.

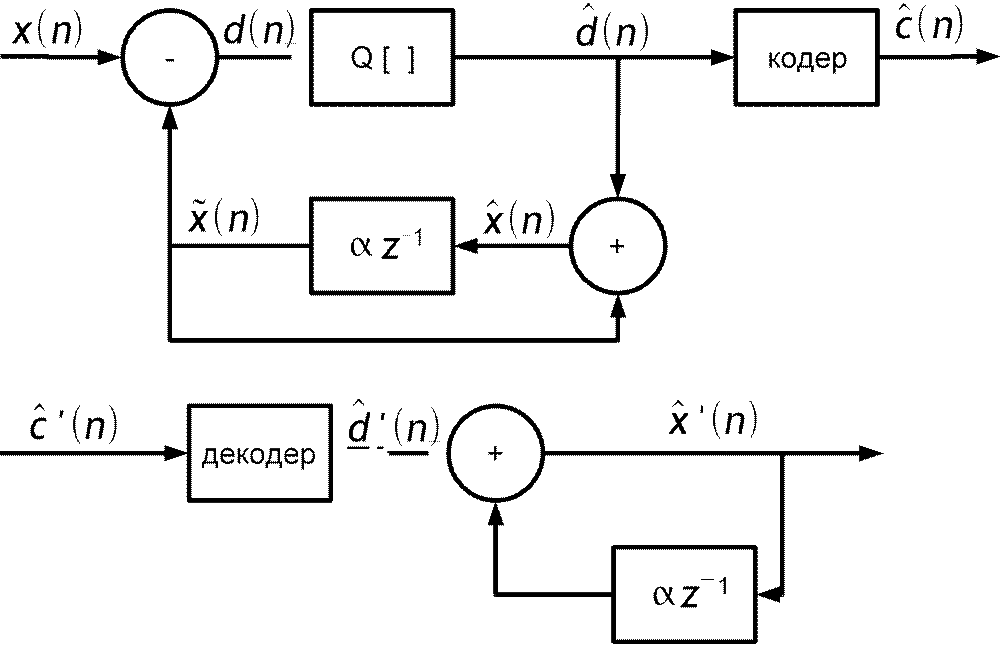
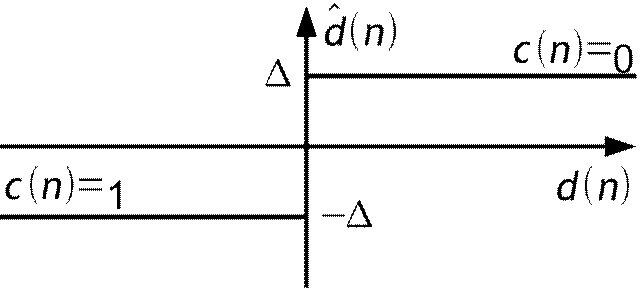
x  n=⋅x  n−1d  n

d  n=x  n−x  n=x  n−x  n−1−e n−1

_≥max dx t

T             dt

Адаптивная дельта-модуляция

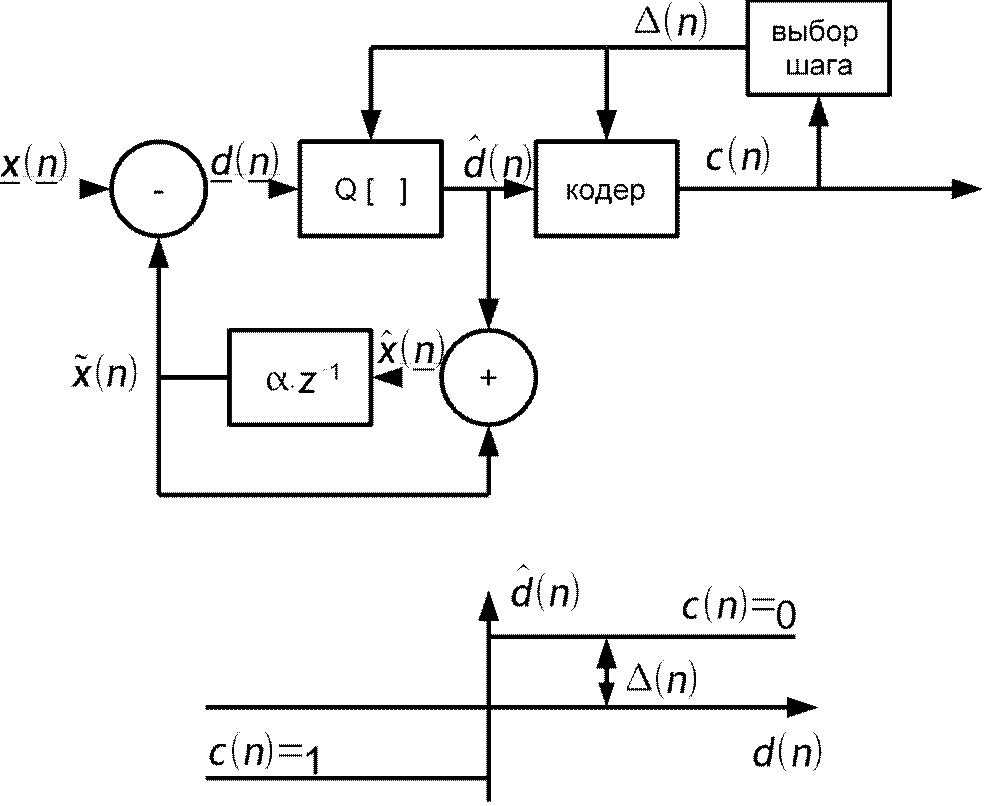
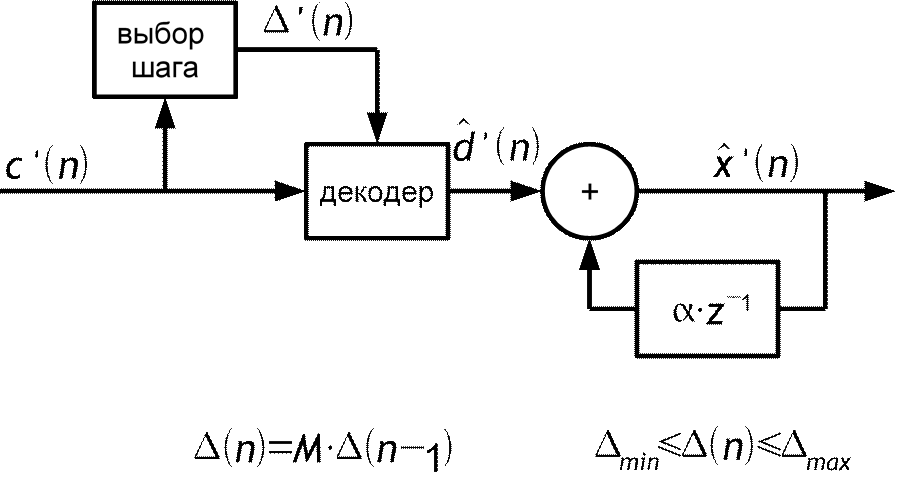
M       множитель определяется исходя из предшествующих кодовых слов:

M=P1   если    c n=c n−1 ; M=Q1   если    c n≠c n−1.

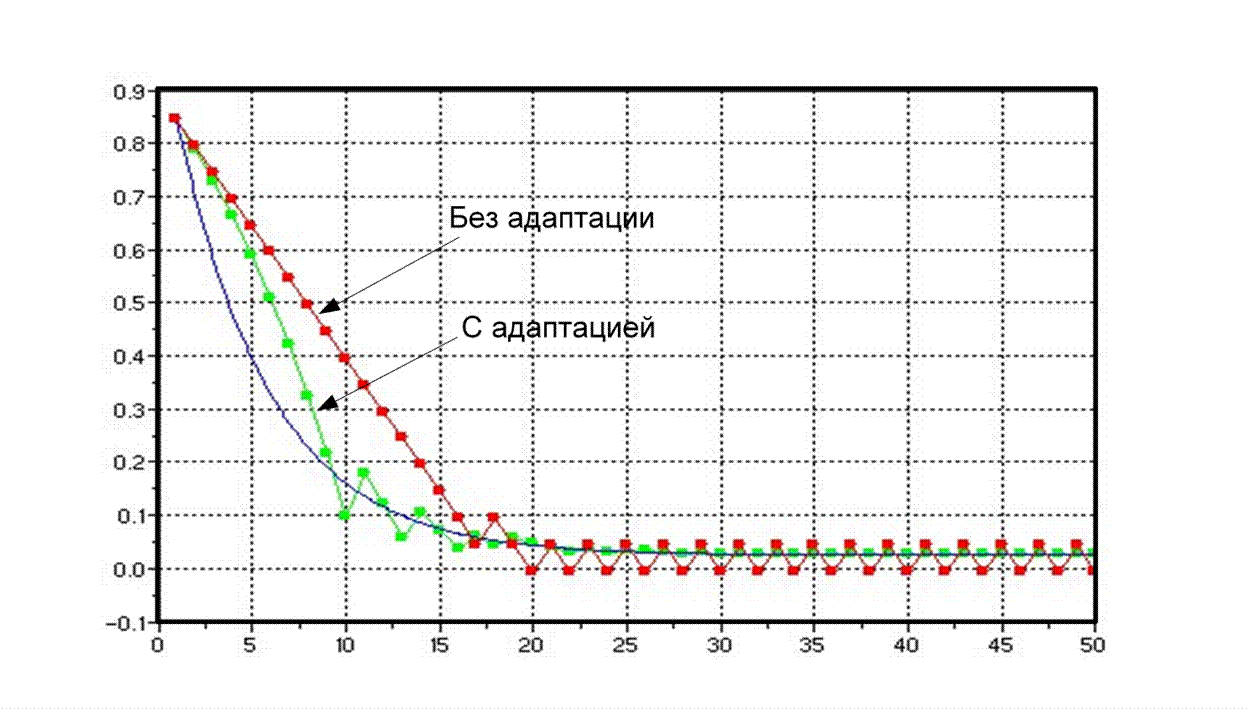
Исследование адаптивной дельта-модуляции позволяет повысить отношение  сигнал-шум квантования на 8..14 дБ по сравнению с линейной дельта-модуляцией.

При этом отношение сигнал шум при адаптивной дельта-модуляции эквивалентно   отношению сигнал шум при m-компандировании РС.

Адаптивная дифференциальная ИКМ (АДИКМ, AD P CM )

Структурная схема с адаптацией по входу шага

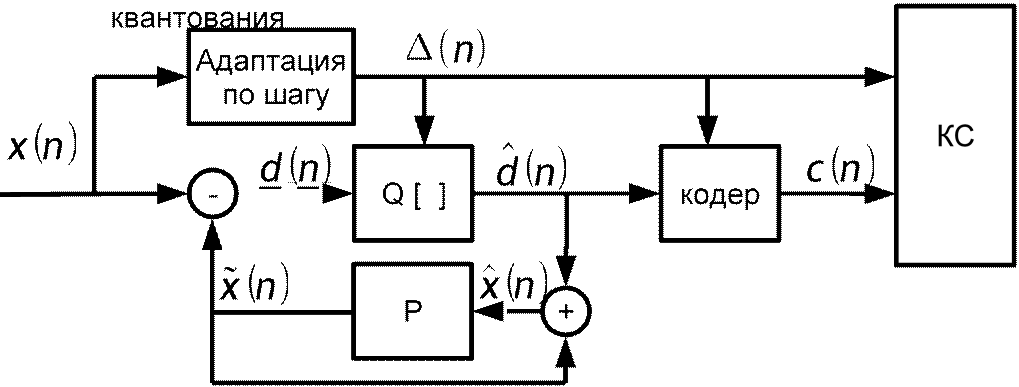
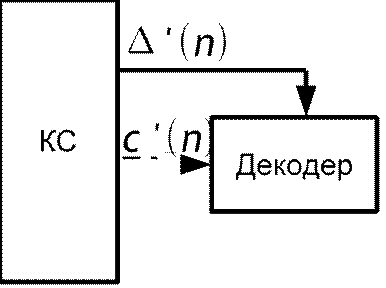                                                                     d ' n               x ' n

АДИКМ по сравнению с m-компандиованием позволят увеличить отношение сигнал-шум квантования на 4..6 дБ.

Структурная схема с адаптацией по выходу шага квантования

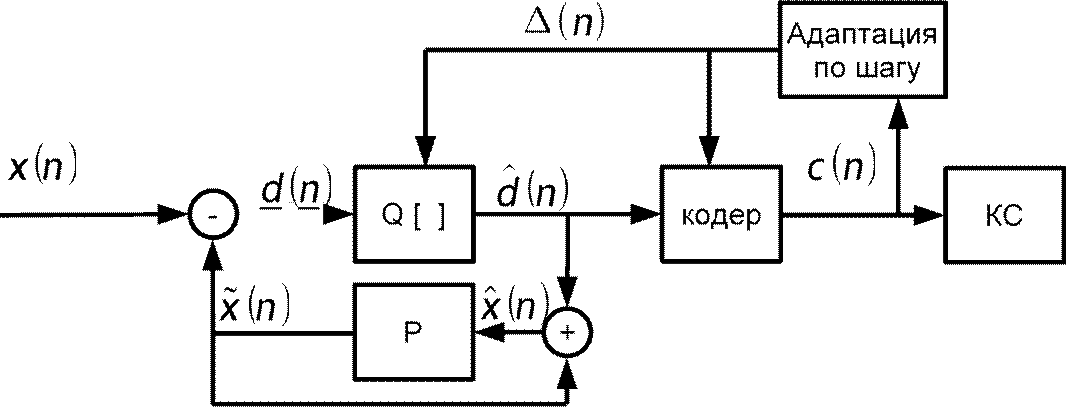
                d ' n          x ' n

АДИКМ с адаптивным предсказателем

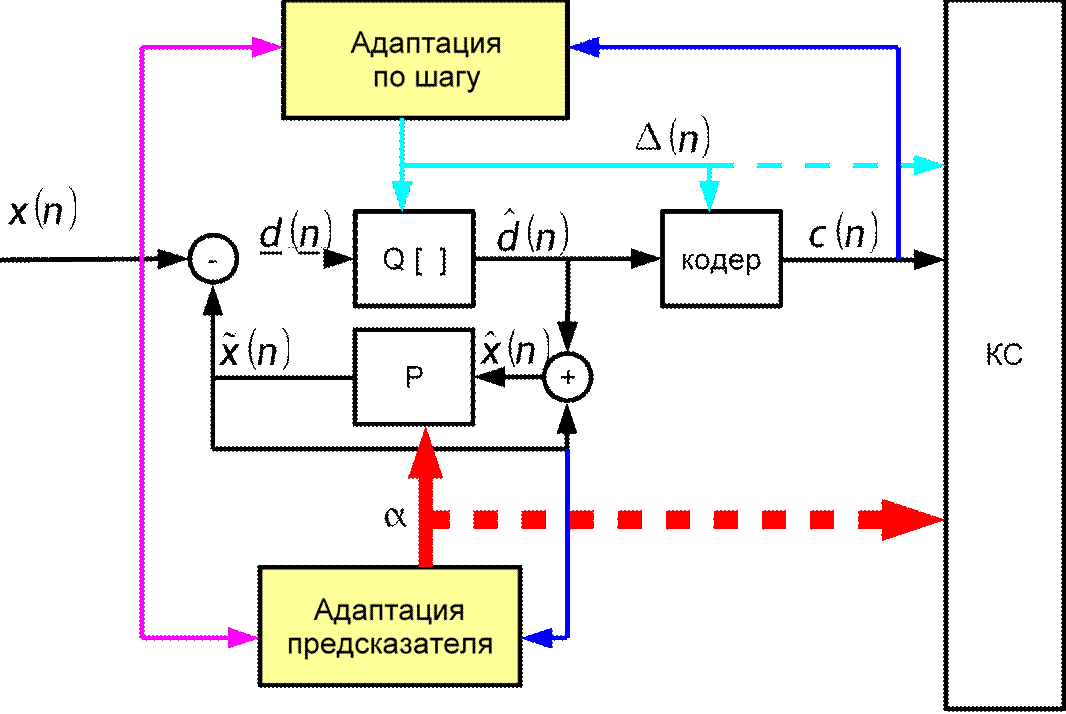
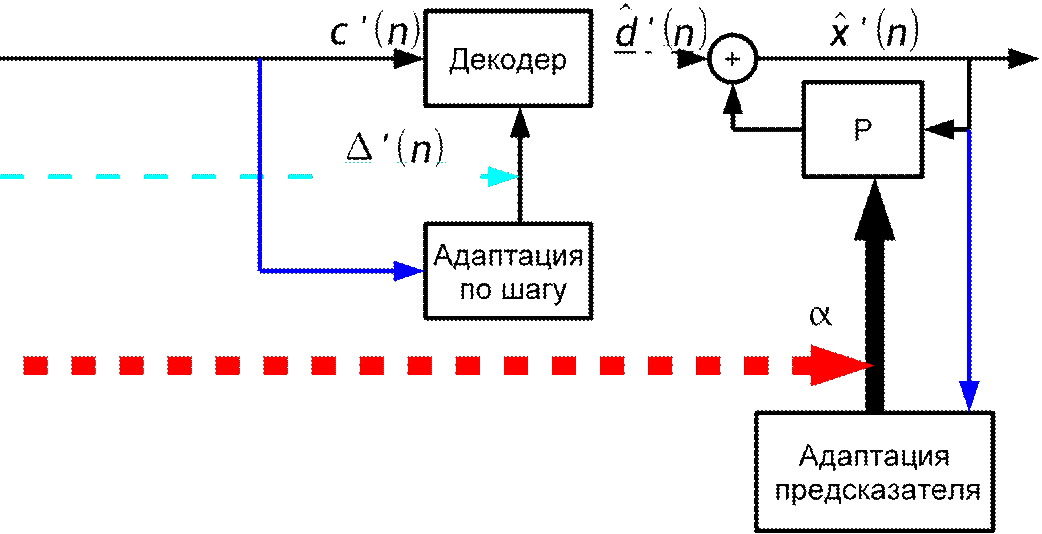
коэффициенты предсказателя зависят от времени (*) прошлой лекции:

P

x n=∑ _kn⋅x n−k ,

k=1

и их можно рассчитывать исходя из уравнения (!!!) решая систему в матричном виде

P

R _x j=∑ _k⋅[R _x j−k;                                           (!!!)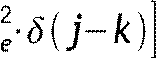

k=1

или в матричной форме _x=С , где

                                         1           1    ⋯ P−1

_С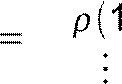      1         ⋯ P−2〛 .

P−1 P

R ^x j

_x j= ₂ ,

_x

При этом оценку коэффициентов предсказания целесообразно вести каждые 10..20 мс

Сравнение способов кодирования РС

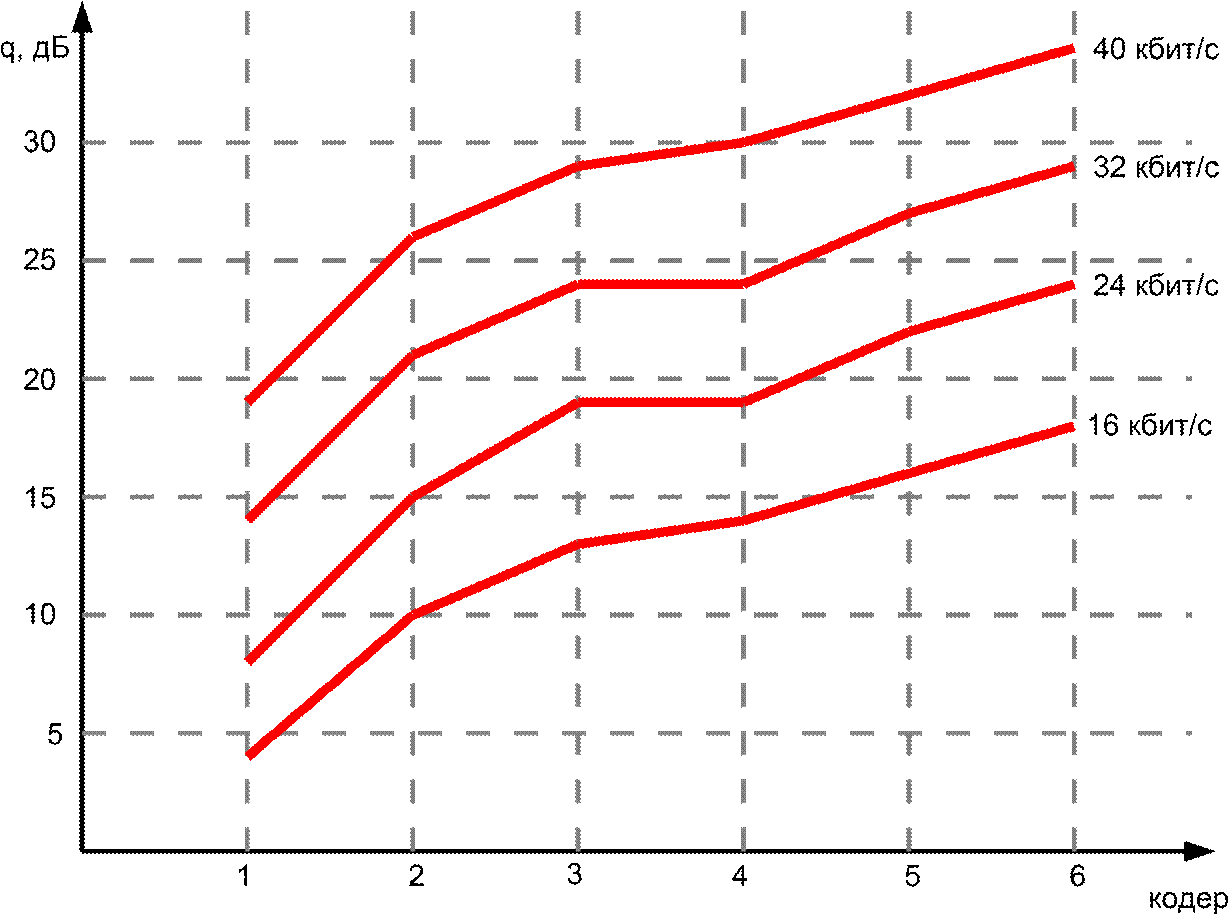
1.  Неадаптивная ИКМ c      - компандированием,        =100

2.  Адаптивная ИКМ с оптимальным гауссовским квантователем и адаптацией по входу  

3.  ДИКМ с предсказателем первого порядка и адаптивным гауссовским квантователем при адаптацией по выходу     

4.  АДИКМ с адаптивным предсказателем первого порядка и адаптивным гауссовским квантователем при адаптацией по выходу     

5.  АДИКМ с  предсказателем четвертого порядка и адаптивным квантователем (распределение Лапласа) при адаптацией по входу     

6.  АДИКМ с  адаптивным предсказателем 12-го порядка и адаптивным квантователем (Гамма-распределение) при адаптацией по входу     

Сжатие сигналов МТКС. Преобразования сигналов

Кодеры сигналов

Кодеры с Субполосные преобразованием кодеры

Дискр. пр. Фурье    Дискр. пр. Фурье Дискр. синусное пр.    Дискр. синусное пр.

Дискр. косинусное пр.   Дискр. косинусное пр.

Пр. Габора    Пр. Габора

Вейвлет-преобр.   Вейвлет-преобр.

Требования к преобразованиям и базисным функциям:

1.  Локализация

2.  Ортогональность

3.  Масштаб 

4.  Эффективные вычислительные процедуры