Обобщенная структурная схема системы передачи информации. Сигналы МТКС и их свойства, страница 2

Разрядность	2	3	4	8	12	16
отношение сигнал-шум, дБ	4,8	10,8	16,8	40,8	64,8	88,8

Пример реализации шума квантования

Выбор количества уровней квантования для РС при равномерном квантовании

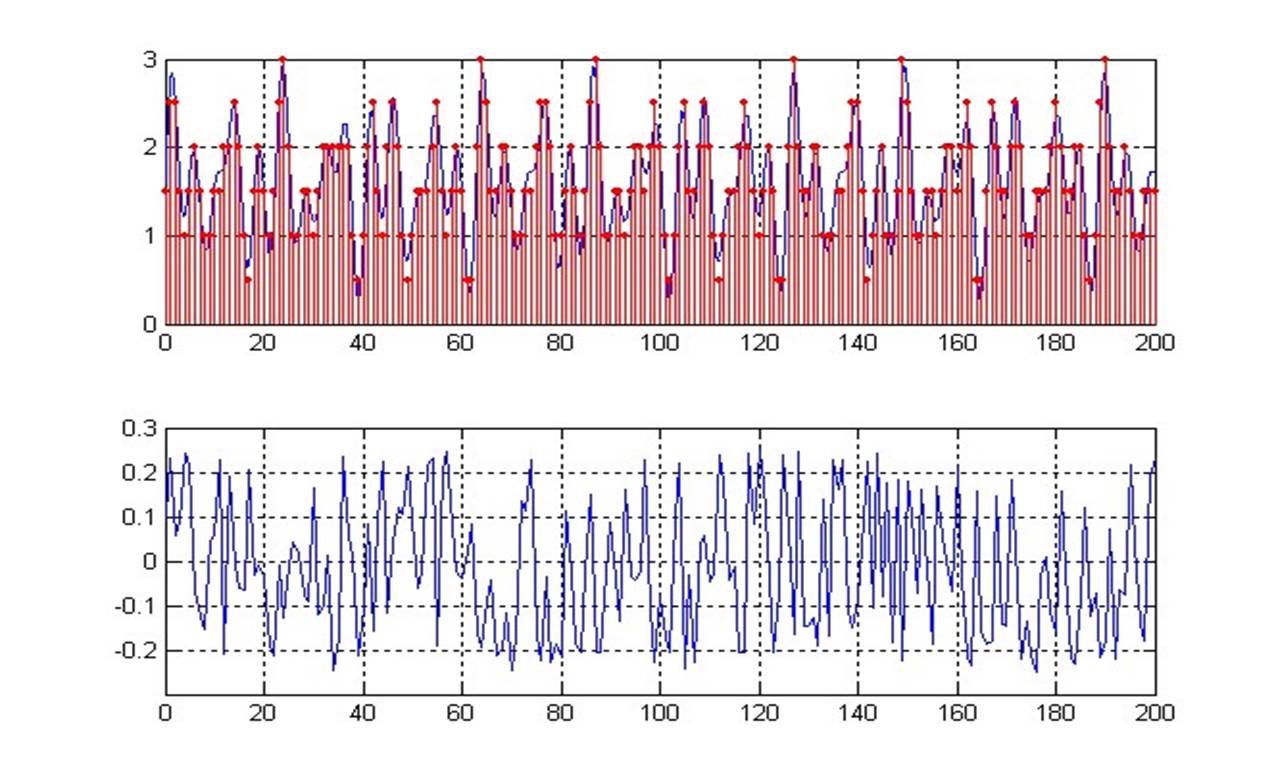
Для выбора количества уровней квантования на основе полученных соотношений  необходимо:

1. Шаг квантования должен быть мал настолько, чтобы шум квантования был белый и некоррелированный с сигналом 2. Диапазон квантования должен быть установлен так, чтобы он перекрывал диапазон сигнала.

Для РС первое условие выполняется если количество уровней квантования равно 64 (6 бит)

При этом для выполнения второго условия необходимо не менее 11 бит представления, поскольку динамический диапазон сигнала может изменяться более чем на 40 дБ Неравномерное квантование РС. Мгновенное компандирование

При квантовании сигналов с большим динамическим диапазоном, вместо квантователя постоянной абсолютной ошибкой, независящей от уровня сигнала, требуется квантователь с постоянной относительной ошибкой.

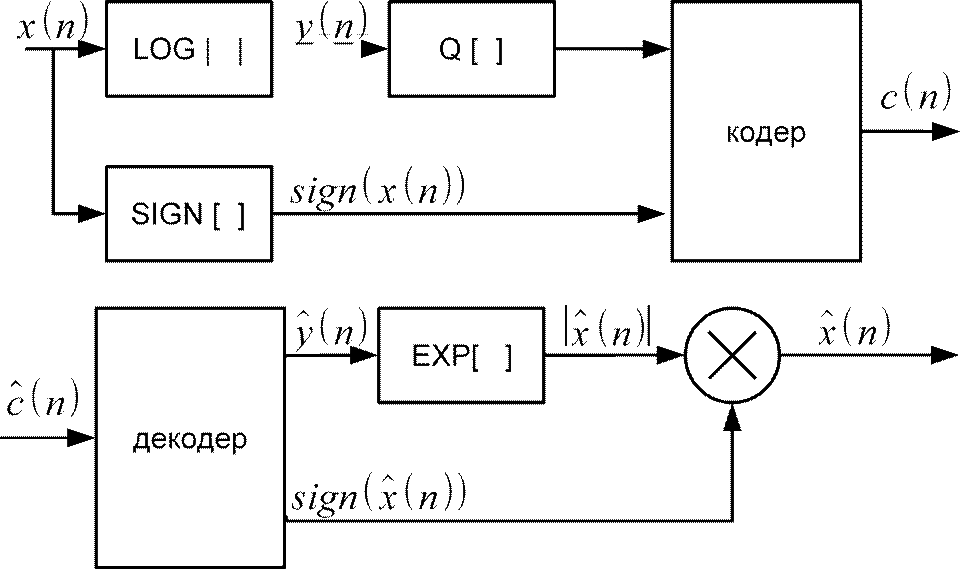
Логарифмическое преобразования входного отсчета:

yn=ln∣xn∣, тогда xn=exp yn⋅signxn, где signxn=1, ecли xn0 ; signxn=−1, ecли xn0. квантованный логарифм: yn=Q[ln∣xn∣]=ln∣xn∣en. Применяем обратное преобразование:

x n=exp yn⋅signxn=∣xn∣⋅signxn⋅expen=...

...=xn⋅expen.

если e(n) мало, то expen≈1en, тогда x n=xn1en=xnxn⋅en=xn f n,

где f n=xn⋅en. Отношение сигнал-шум: 2x 1

q= ₂ = ₂ ,  f e

поскольку ²_f

X ynx n.

ln1

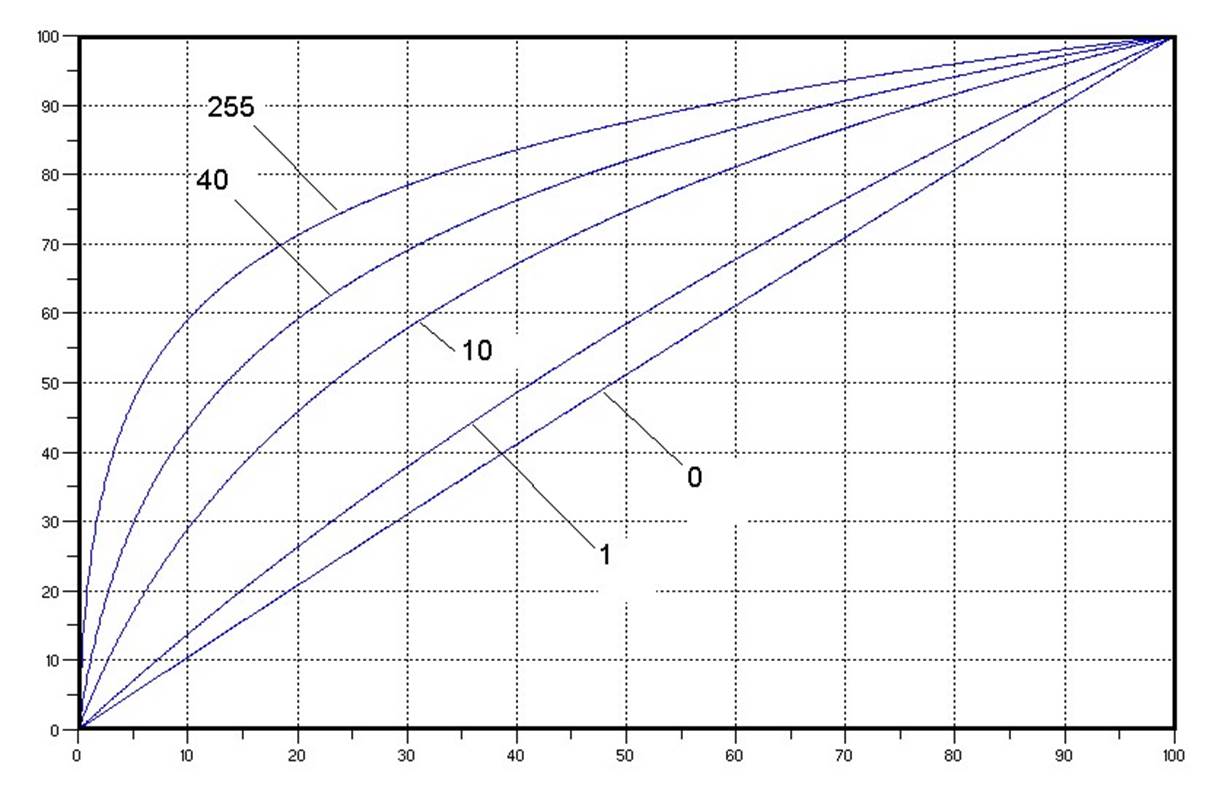
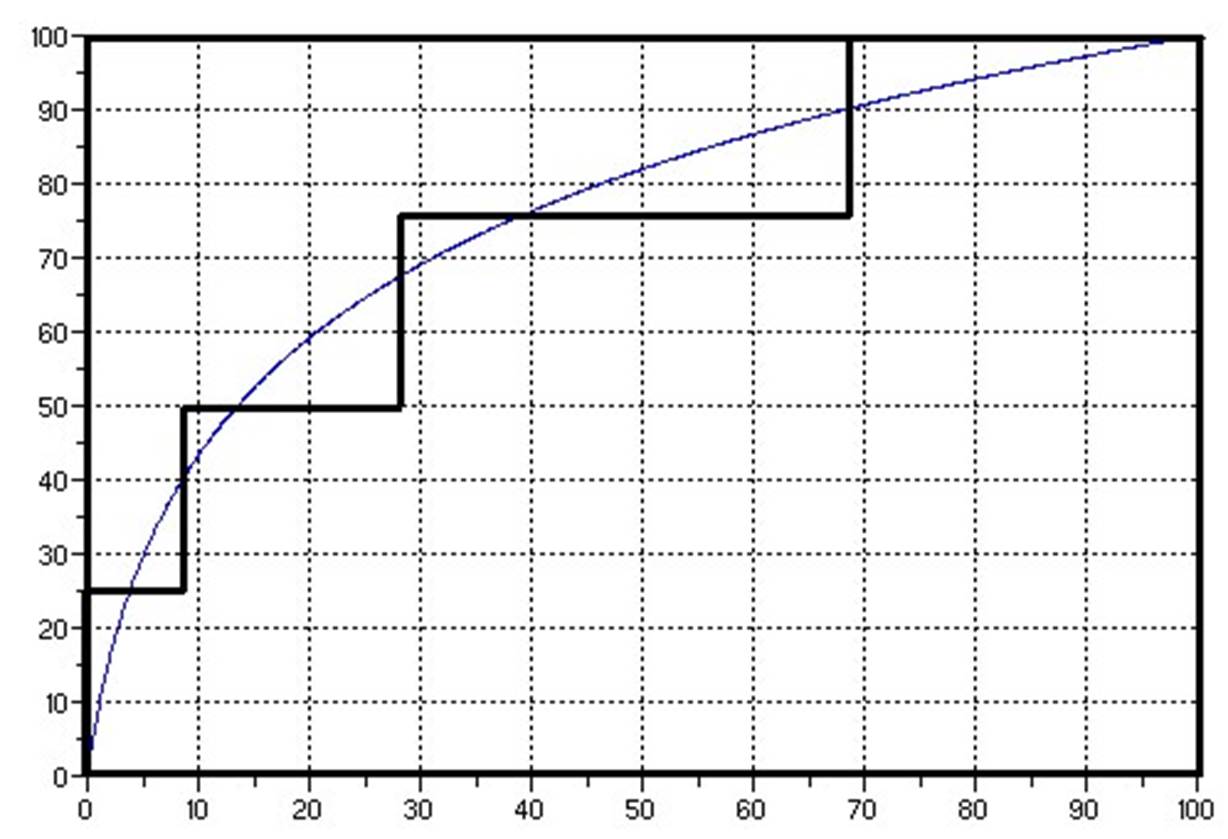
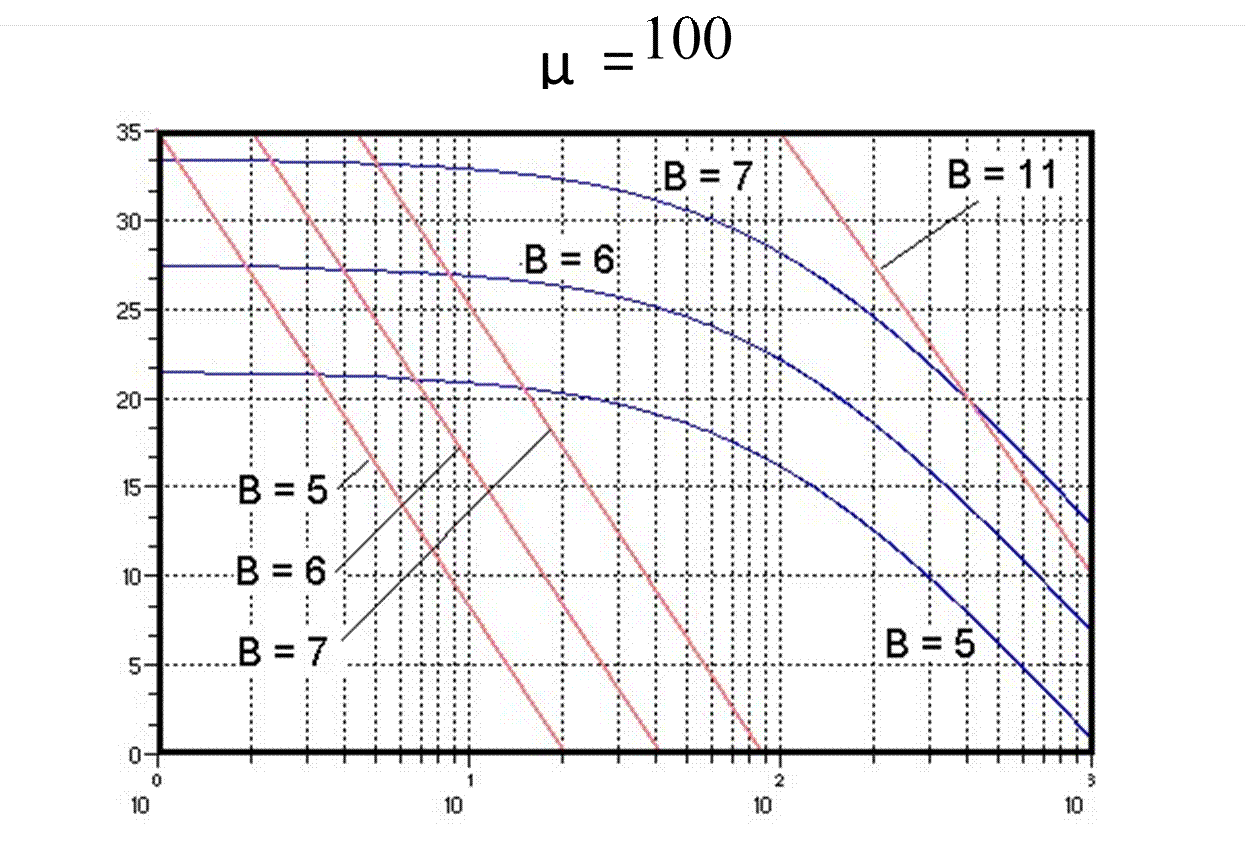
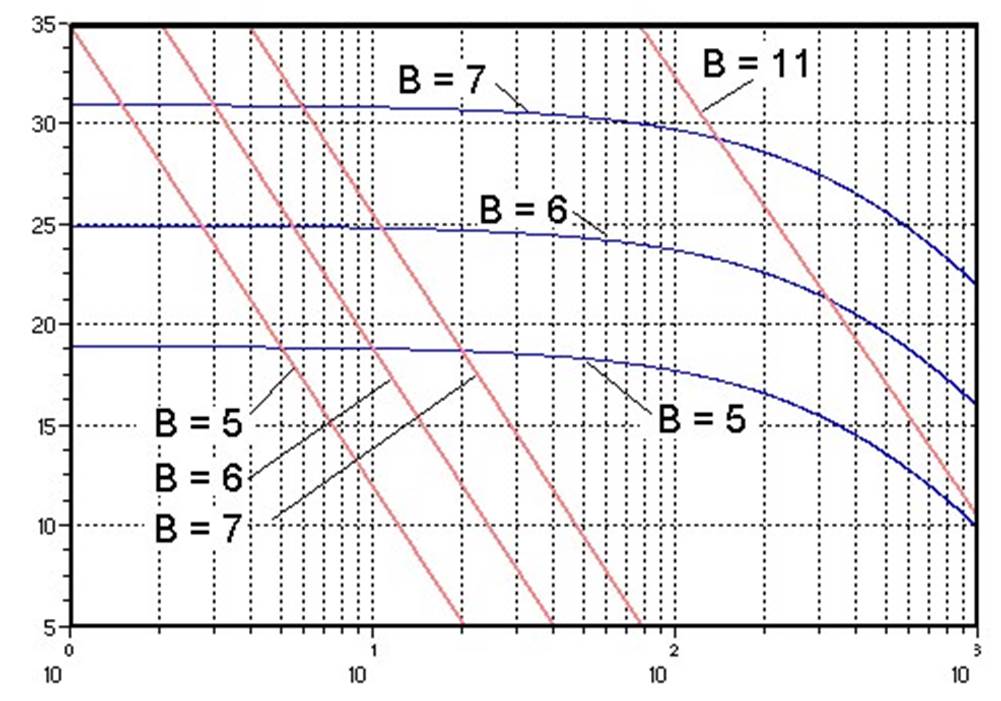
Отношениесигнал-шумвэтомслучаеимеетвид q = 6 B + 4.77 − 20 ⋅ lg (ln 1( + μ)) −

⎡        ⎛ X             ^⎞2           ⎛ X         ^⎞⎤

−10 ⋅ lg ⎢1 + ⎜  max ⎟ + 2 ⎜   max ⎟⎥ . ⎢_⎣ ⎝ μσ_x    ⎠  ⎝ μσ_x ⎠⎥_⎦

Зависитот:

1.  μ

X

2.  Отношения _σ^maxx

μ=500

Оптимальноеквантование

Дисперсия шума квантования:

σ_e² =E e n_⎣⎡ ²( )⎤_⎦=E x n x n⎡_⎣( ( )− ˆ( ))²⎤_⎦,

Пусть имеется M уровней квантования (М - четное)

⎧                                ⎫

⎨xˆ_−M+¹,...,x xˆ₋₁, ˆ₁,...,xˆ_M ⎬,            x^ˆ_{±M /2} =±∞

⎩ 2                                         2 ⎭

Дисперсию шума квантования можно вычислить через ФПВ шума квантования как ∞ .

−∞

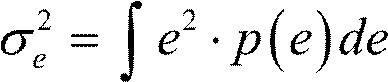ФПВ шума квантования сложно оценить на практике, поэтому дисперсию выражают через ФПВ исходного сигнала

M /2        ^xi

2

.

i=−M /2 1+ ^x_i−1

Если p(−x)= p x( ) , то

M /2 ^xi

σ_e² = 2∑ ∫ (x xˆ_i − )² ⋅ p x dx( )                                 . (***)

i=1 xi−1

Для нахождения оптимальных интервалов квантования,а также уровней квантования, необходимо продифференцировать (***) и приравнять к 0. 

x_i ∫ (xˆ_i − x)⋅ p x dx( )   = 0,  i =1,2,...,M /2;

xi₋1

x_i = (xˆ_i + xˆ_i+1 )2, i =1,2,...,(M /2)−1; x₀ = 0; x±M /2 = ±∞.

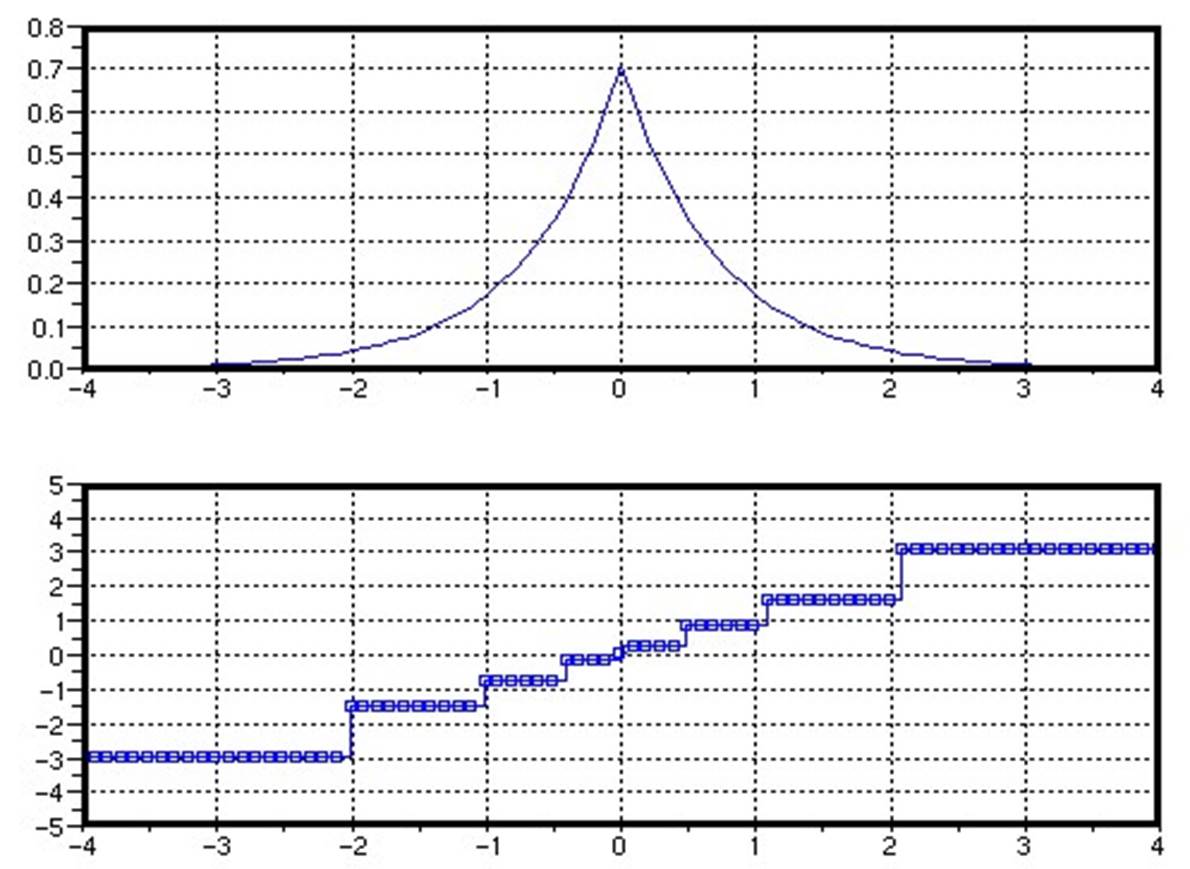
1.  Оптимальные пороги равны полусумме соответствующих уровней квантования

2.  Оптимальные уровни квантования есть среднее значение ФПВ между порогами

3.  Система нелинейная и решается численно

4.  Для равномерного распределения оптимально равномерное квантование

Адаптивное квантование