Статистические величины. Использование их в медицине. Динамические ряды. Способы их выравнивания и анализа: Учебно-методическое пособие, страница 4

При изучении варьирующего признака нельзя ограничиваться только вычислением средних величин. Необходимо вычислять и показатели, характеризующие степень разнообразия изучаемых признаков. Величина того или иного количественного признака неодинакова у всех единиц статистической совокупности.

Характеристикой вариационного ряда является среднее квадратичное отклонение (), которое показывает разброс (рассеивание) изучаемых признаков относительно средней арифметической, т.е. характеризует колеблемость вариационного ряда. Оно может определяться непосредственным способом по формуле:

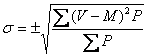
Среднее квадратичное отклонение равняется квадратному корню из суммы произведений квадратов отклонений каждой варианты от средней арифметической (V–M)² на свои частоты деленной на сумму частот ().

Пример вычисления: определить среднее число больничных листов, выдаваемых в поликлинике за день (таблица 3).

Т а б л и ц а 3

Число больничных листов, выданных врачом за день (V)	Число врачей (Р)	VP	V–M	(V–M)2	(V–M)2P
4	2	8	-2	4	8
5	4	20	-1	1	4
6	9	54	0	0	0
7	3	21	1	1	3
8	2	16	2	4	8

                                               n=20             120                                   23

;

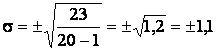
В знаменателе при числе наблюдений менее 30 необходимо от  отнимать единицу.

Если ряд сгруппирован с равными интервалами, тогда можно определить среднее квадратичное отклонение по способу моментов:

,

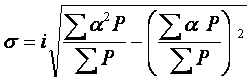где i — величина интервала;

    — условное отклонение от условной средней;

P         — частоты вариант соответствующих интервалов;

 — общее число наблюдений.

Пример вычисления: Определить среднюю длительность пребывания больных на терапевтической койке (по способу моментов) (таблица 4):

Т а б л и ц а 4

Число дней пребывания на койке (V)	Число больных (Р)
5-9	17	-2	-34	68
10-14	44	-1	-44	44
15-19	193	0	0	0
20-24	131	1	131	131
25-29	12	2	24	48
30-34	3	3	9	27

                                                  400                                  86               318

;

.

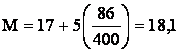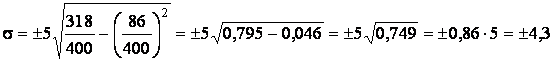Бельгийский статистик А. Кетле обнаружил, что вариации массовых явлений подчиняются закону распределения ошибок, открытому почти одновременно К. Гауссом и П. Лапласом. Кривая, отображающая это распределение, имеет вид колокола. По нормальному закону распределения колеблемость индивидуальных значений признака находится в пределах , что охватывает 99,73% всех единиц совокупности.

Подсчитано, что если к средней арифметической прибавить и отнять 2, то в пределах полученных величин находится 95,45% всех членов вариационного ряда и, наконец, если к средней арифметической прибавить и отнять 1, то в пределах полученных величин будут находиться 68,27% всех членов данного вариационного ряда. В медицине с величиной 1 связано понятие нормы. Отклонение от средней арифметической больше, чем на 1, но меньше, чем на 2 является субнормальным, а отклонение больше, чем на 2 ненормальным (выше или ниже нормы).

В санитарной статистике правило трех сигм применяется при изучении физического развития, оценке деятельности учреждений здравоохранения, оценке здоровья населения. Это же правило широко применяется в народном хозяйстве при определении стандартов.

Таким образом, среднее квадратичное отклонение служит для:

― измерения дисперсии вариационного ряда;

― характеристики степени разнообразия признаков, которые определяются коэффициентом вариации:

Если коэффициент вариации более 20% — сильное разнообразие, от 20 до 10% — среднее, менее 10% — слабое разнообразие признаков. Коэффициент вариации в известной мере является критерием надежности средней арифметической.

ДИНАМИЧЕСКИЙ РЯД, ЕГО АНАЛИЗ И СПОСОБЫ

ВЫРАВНИВАНИЯ

Динамический ряд ― ряд однородных сопоставимых величин, показывающих изменение изучаемого явления во времени. Это статистическая форма отображения развития явлений во времени. Числа, составляющие динамический ряд, принято называть уровнями ряда. Уровни ряда могут быть представлены абсолютными числами, относительными и средними величинами.

Интервальный ряд состоит из последовательного ряда чисел, характеризующих изменение явления на определенный период (по времени).

Моментный ряд состоит из величин, определяющих размеры явления не за какой-либо отрезок времени, а на определенную дату — момент.

Для более глубокого понимания сути развития общественных явлений исчисляют такие показатели динамического ряда, как абсолютный прирост, темп прироста, темп роста, абсолютное значение 1% прироста.

Абсолютным приростом называют разницу между каждым последующим уровнем и уровнем предыдущим. Абсолютный прирост может быть положительным и отрицательным.

Темпом роста называется отношение каждого последующего уровня к предыдущему, выраженному в процентах.

Темпом прироста называется отношение абсолютного прироста к предыдущему уровню, принятому за 100%.

Так как каждому относительному показателю соответствуют определенные абсолютные величины, то при изучении темпов прироста нужно обязательно учитывать, какая абсолютная величина соответствует каждому проценту прироста, каково его содержание. Для этого исчисляется такой показатель, как абсолютное значение одного процентаприроста. Он определяется как частное от деления абсолютного прироста за определенный период на темп прироста в процентах за этот же период.

Для иллюстрации расчетов рассмотренных статистических показателей приведем ряд динамики.

Приведем пример. Необходимо дать анализ динамики рождаемости в определенном районе (таблица 5).

Т а б л и ц а 5 — Динамика рождаемости в регионе за 1996–2005гг.