4. Четные и нечетные.
В чётных вариационных рядах сумма частот или общее число наблюдений выражено чётным числом, в нечётных ― нечётным.
5. Симметричные и асимметричные.
В симметричном вариационном ряду все виды средних величин совпадают или очень близки (мода, медиана, среднее арифметическое).
В зависимости от характера изучаемых явлений, от конкретных задач и целей статистического исследования, а также от содержания исходного материала, в санитарной статистике применяются следующие виды средних величин:
· структурные средние (мода, медиана);
· средняя арифметическая;
· средняя гармоническая;
· средняя геометрическая;
· средняя прогрессивная.
Мода (Мо) — величина варьирующего признака, которая более часто встречается в изучаемой совокупности т.е. варианта, соответствующая наибольшей частоте. Находят ее непосредственно по структуре вариационного ряда, не прибегая к каким-либо вычислениям. Она обычно является величиной очень близкой к средней арифметической и весьма удобна в практической деятельности.
Медиана (Ме) — делящая вариационный ряд (ранжированный, т.е. значения вариант располагаются в порядке возрастания или убывания) на две равные половины. Медиана вычисляется при помощи так называемого нечетного ряда, который получают путем последовательного суммирования частот. Если сумма частот соответствует четному числу, тогда за медиану условно принимают среднюю арифметическую из двух средних значений.
Мода и медиана применяются в случае незамкнутой совокупности, т.е. когда наибольшая или наименьшая варианты не имеют точной количественной характеристики (например, до 15 лет, 50 и старше и т.п.). В этом случае среднюю арифметическую (параметрические характеристики) рассчитать нельзя.
Средняя арифметическая — самая распространенная величина. Средняя арифметическая обозначается чаще через М.
Различают среднюю арифметическую простую и взвешенную.
Средняя арифметическая простая вычисляется:
― в тех случаях, когда совокупность представлена простым перечнем знаний признака у каждой единицы;
― если число повторений каждой варианты нет возможности определить;
― если числа повторений каждой варианты близки между собой.
Средняя арифметическая простая исчисляется по формуле:
![]() ,
,
где V — индивидуальные значения признака; n —
число индивидуальных значений; ![]() — знак суммирования.
— знак суммирования.
Таким образом, простая средняя представляет собой отношение суммы вариант к числу наблюдений.
Пример: определить среднюю длительность пребывания на койке 10 больных пневмонией:
16 дней — 1 больной; 17–1; 18–1; 19–1; 20–1; 21–1; 22–1; 23–1; 26–1; 31–1.
![]() койко-дня.
койко-дня.
Средняя арифметическая взвешенная исчисляется в тех случаях, когда индивидуальные значения признака повторяются. Ее можно вычислять двояким способом:
1. Непосредственным (среднеарифметическим или прямым способом) по формуле:
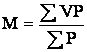 ,
,
где P — частота (число случаев) наблюдений каждой варианты.
Таким образом, средняя арифметическая взвешенная представляет собой отношение суммы произведений вариант на частоты к числу наблюдений.
2. С помощью вычисления отклонений от условной средней (по способу моментов).
Основой для вычисления взвешенной средней арифметической является:
― сгруппированный материал по вариантам количественного признака;
― все варианты должны располагаться в порядке возрастания или убывания величины признака (ранжированный ряд).
Для вычисления по способу моментов обязательным условием является одинаковый размер всех интервалов.
По способу моментов средняя арифметическая вычисляется по формуле:
 ,
,
где Мо — условная средняя, за которую чаще принимают величину признака, соответствующую наибольшей частоте, т.е. которая чаще повторяется (Мода).
i — величина интервала.
a — условное отклонение от условий средней, представляющее собой последовательный ряд чисел (1, 2 и т.д.) со знаком + для вариант больших условной средней и со знаком–(–1, –2 и т.д.) для вариант, которые ниже условной средней. Условное же отклонение от варианты, принятой за условную среднюю равно 0.
P — частоты.
![]() — общее
число наблюдений или n.
— общее
число наблюдений или n.
Пример: определить средний рост мальчиков 8 лет непосредственным способом (таблица1).
Т а б л и ц а 1
|
Рост в см |
Число мальчиков P |
Центральная варианта V |
VP |
|
115-116 |
2 |
116 |
232 |
|
117-118 |
7 |
118 |
826 |
|
119-120 |
21 |
120 |
2520 |
|
121-122 |
33 |
122 |
4026 |
|
123-124 |
21 |
124 |
2604 |
|
125-126 |
12 |
126 |
1512 |
|
127-128 |
3 |
128 |
384 |
|
129-130 |
1 |
130 |
130 |
n = 100 12234
Центральная варианта ― середина интервала ― определяется как полу сумма начальных значений двух соседних групп:
![]() ;
; ![]() и т.д.
и т.д.
Произведение VP получают путем умножения центральных
вариант на частоты ![]() ;
; ![]() и
т.д. Затем полученные произведения складывают и получают
и
т.д. Затем полученные произведения складывают и получают ![]() , которую делят на число наблюдений
(100) и получают среднюю арифметическую взвешенную.
, которую делят на число наблюдений
(100) и получают среднюю арифметическую взвешенную.
![]() см.
см.
Эту же задачу решим по способу моментов, для чего составляется следующая таблица 2:
Т а б л и ц а 2
|
Рост в см (V) |
Число мальчиков P |
а |
аP |
|
115–116 |
2 |
-3 |
-6 |
|
117–118 |
7 |
-2 |
-14 |
|
119–120 |
21 |
-1 |
-21 |
|
121–122 |
33 |
0 |
0 |
|
123–124 |
21 |
1 |
21 |
|
125–126 |
12 |
2 |
24 |
|
127–128 |
3 |
3 |
9 |
|
129–130 |
1 |
4 |
4 |
n=100 ![]()
В качестве Мо
принимаем 122, т.к. из 100 наблюдений у 33 человек рост был 122см. Находим
условные отклонения (a) от условной средней в соответствии с вышесказанным.
Затем получаем произведение условных отклонений на частоты (aP) и суммируем
полученные величины (![]() ). В итоге получится 17. Наконец,
данные подставляем в формулу:
). В итоге получится 17. Наконец,
данные подставляем в формулу:
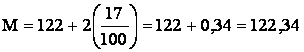
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.