Социология и политология \ Социология

Проверка нормального распределения переменных "Возраст" и "Коэффициент К" с помощью теста Колмогорова - Смирнова

Страницы работы

9 страниц (Word-файл)

Скачать файл

Содержание работы

Отчет №6

Для построения нового коэффициента К сначала используем функцию COUNT для подсчета количества людей, которые затруднились ответить(99). После этого с помощью COMPUTE строим коэффициент К, который будет равен «количество ответов «99», деленное на количество вопросов» С помощью теста Колмогорова – Смирнова проверяем нормально ли распределены возраст и коэффициент К.

Получаем следующие данные:

Проверка нормального распределения переменных «возраст» и «коэффициент К» с помощью теста Колмогорова - Смирнова

		возраст	К
N		1175	1175
Normal Parameters(a,b)	Mean	44,74638	1,041702
	Std. Deviation	17,04575	0,954214
Most Extreme Differences	Absolute	0,08651	0,206344
	Positive	0,08651	0,206344
	Negative	-0,05831	-0,15812
Kolmogorov-Smirnov Z		2,965407	7,07312
Asymp. Sig. (2-tailed)		0,000	0,000
a	Test distribution is Normal.
b	Calculated from data.

Отклонение от нормального распределения считается существенным при значении Asymp. Sig. (2-tailed)< 0,05; В наше случае, 0,000< 0,05, то есть распределение ненормально. Адекватными коэффициентами корреляции будут коэффициенты ранговой корреляции (коэффициента ранговой корреляции Кэндала).

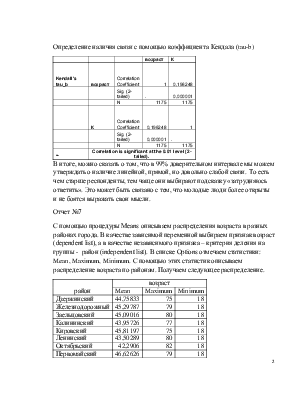
Определение наличия связи с помощью коэффициента Кендала (tau-b)

			возраст	К
Kendall's tau_b	возраст	Correlation Coefficient	1	0,196248
		Sig. (2-tailed)	.	0,000001
		N	1175	1175
	К	Correlation Coefficient	0,196248	1
		Sig. (2-tailed)	0,000001	.
		N	1175	1175
**	Correlation is significant at the 0.01 level (2-tailed).

В итоге, можно сказать о том, что в 99% доверительном интервале мы можем утверждать о наличие линейной, прямой, но довольно слабой связи. То есть чем старше респонденты, тем чаще они выбирают подсказку «затрудняюсь ответить». Это может быть связано с тем, что молодые люди более открыты и не боятся выражать свои мысли.

Отчет №7

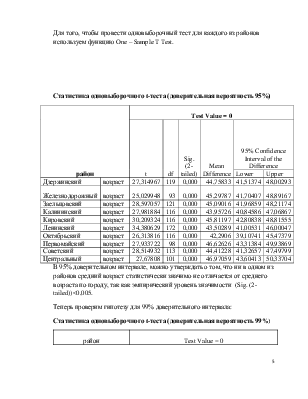
С помощью процедуры Means описываем распределения возраста в разных районах города. В качестве зависимой переменной выбираем признак возраст (dependent list), а в качестве независимого признака – критерия деления на группы - район (independent list). В списке Options отмечаем статистики: Mean, Maximum, Minimum. С помощью этих статистик описываем распределение возраста по районам. Получаем следующее распределение.

район	возраст
район	Mean	Maximum	Minimum
Дзержинский	44,75833	75	18
Железнодорожный	45,29787	79	18
Заельцовский	45,09016	80	18
Калининский	43,95726	77	18
Кировский	45,81197	75	18
Ленинский	43,50289	80	18
Октябрьский	42,2906	82	18
Первомайский	46,62626	79	18
Советский	44,41228	77	18
Центральный	46,97059	75	18
Total	44,74638	82	18

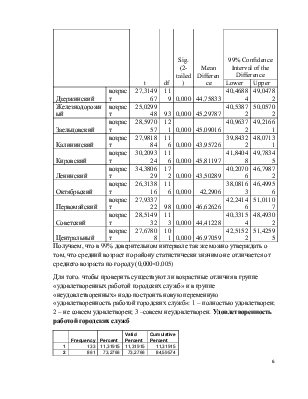
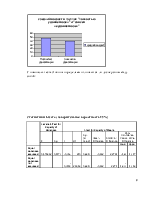
Для описания воспользуемся опциями Excel. Строим график, который будет отражать минимальный и максимальный возраст по района с наложением прямой «средний возраст»

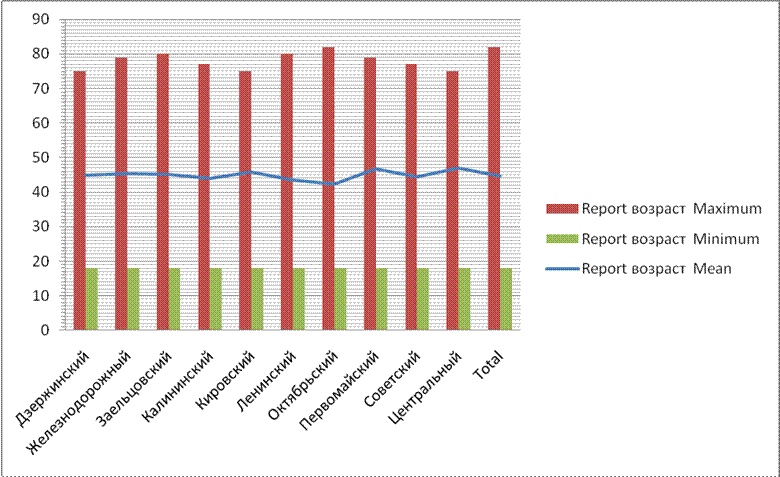
В результате можно сказать о том, что минимальный возраст во всех районах одинаковый и равен 18 годам. Самый большой максимальный возраст в Октябрьском районе, возраст респондента составляет 82 года. Но несмотря на это, средний возраст в Октябрьском районе равен 42 годам. Это говорит о том, что в этом районе проживают люди с большим возрастным разбросом. В Дзержинском и Кировском районах зарегистрирован максимальный возраст – 75 лет. Этот возраст является самым «молодым» среди максимальных возрастов по городу.