Параметры состояния рабочего тела. Термодинамический процесс и законы термодинамики. Реальные газы. Влажный воздух. Физические свойства воды и водяного пара на линии насыщения, страница 2

а)  Р_аб = 740 мм рт.ст.,            h = (500 + 200·n);           в)Р_аб = 790 мм рт.ст., 

б)  Р_аб  = 770 мм рт.ст.,           h = (4000 + 200·n);          h = (2000 + 150·n).

Результаты расчетов привести в различных размерностях: ат (кГ/см²), кПа (МПа), бар.

Рекомендации: Расчет давлений произвести по зависимостям (1.6), (1.7), размерности пересчитываются по зависимостям (1.2 – 1.5).

Задача № 1.3

Рассчитать температуру воздуха в атмосфере на высоте (м):

а) (500 + 200·n)     и    (7000 + 300·n);                  в) (2000 + 150·n)   и

б) (4000 + 200·n)   и    (12000 + 300·n);                (10000 + 150·n).

Результаты расчетов привести в различных размерностях: К, ^оС, F. Сравнить полученные результаты.

Рекомендации: Температура воздуха находится по зависимости (1.12), пересчет размерностей – по (1.11).

Задача № 1.4

Рассчитать плотность морской воды, если в 1 л воды растворено морских солей:

а) m_c=(10 + 1·n), г;          б) m_c= (25 + 1·n), г;                 в) m_c= (35 + 2·n), г.

Плотность пресной воды ρ = 1000 кг/м³, 1 л = 1 дм³, 1 м³ = 10³ дм³.

Рекомендации: Рассчитать массу солей в 1 м³ воды (кг), суммировать ее с массой пресной воды, по (1.13) найти плотность.            

Задача № 1.5

Определить общую силу, которая сжимает вакуумную камеру с размерами: диаметр d = 0,5 м и высотой h = 0,6 м, если в ней необходимо поддерживать абсолютное давление Р_аб = (10 + 5∙n) кПа, а барометрическое давление составляет

а)  725 мм рт.ст.;                      б)  810 мм рт.ст.;            б)  760 мм рт.ст.

Рекомендации: Вакуумметрическое давление (разность абсолютного внутри и барометрического снаружи) находится по (1.8), затем по (1.1) рассчитывается сила F.

Задача № 1.6

Рассчитать вакуумметрическое давление  (которое необходимо откачать из сосуда), если сосуд находится в горах на высоте h, а абсолютное давление в нем необходимо поддерживать Р_аб = (0,1 + 0,05∙n);

а)  h = 1,5 км;                           б)  h = 1,2 км;                 в)  h = 1,8 км.

Результаты расчетов привести в различных размерностях: ат (кГ/см²), кПа (МПа), бар.

Рекомендации: Расчет барометрического давления произвести по (1.6), вакуумметрического – по (1.8).

Тема 2-3: термодинамический процесс и законы

термодинамики

По уравнению Майера

,                                               (2.1)

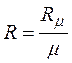                                        .                                                       (2.2)

Здесь R_μ = 8314 Дж/(моль·К) – универсальная газовая постоянная; μ – молекулярная масса, кг/моль.

Средняя теплоемкость газа (изобарная или  изохорная) в диапазоне температур  t₁ и t₂ определяется по зависимости

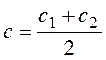,                                                 (2.3)

где с₁ и с₂ – теплоемкости газа при температурах t₁ и t₂, ^оС.

Таблица 2.1.

Средняя изобарная теплоемкость газов

в диапазоне от t=0 ⁰С до 1500 ⁰С

( в формулах t – ⁰С)

Универсальное уравнение состояния газа

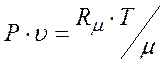.                                               (2.4)

Объемная доля газовой смеси определяется

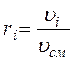.                                                          (2.5)

Молекулярная масса и теплоемкость смеси определяются по

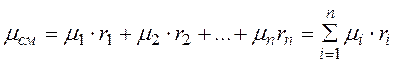                      (2.6)

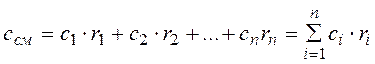                          (2.7)

Внутренняя энергия – функция состояния системы тел, представляющая собой совокупность всех видов энергии, заключенных в данной системе тел (кинетическая и потенциальная энергия молекул, колебательное движение молекул), с повышением температуры Т и давления Р, а также с понижением удельного объема внутренняя энергия ΔU повышается.

При изохорной теплоемкости (Дж/кг·К) , тогда внутренняя энергия рассчитывается (Дж/кг)

.                             (2.8)