Построение математической модели методом ортогонального центрального композиционного плана (ОЦКП)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Дальневосточный федеральный университет»

Школа естественных наук

Базовая кафедра химических и ресурсосберегающих технологий

Отчет по лабораторной работе № 2

«Построение математической модели методом ортогонального центрального композиционного плана (ОЦКП)»

работу проверил: ассистент	работу выполнил              студент группы Б8321

Владивосток

2015

Содержание задания(вариант №5):

При проведении планового эксперимента для четырех факторов получены следующие результаты

№ опыта	х0	х1	х2	х3	х4	у
1	1	1	1	1	1	71,94
2	1	-1	-1	1	1	43,50
3	1	-1	1	1	1	58,527
4	1	1	-1	1	1	72,08
5	1	1	1	-1	1	57,69
6	1	-1	-1	-1	1	45,77
7	1	-1	1	-1	1	47,95
8	1	1	-1	-1	1	59,31
9	1	1	1	1	-1	37,475
10	1	-1	-1	1	-1	54,47
11	1	-1	1	1	-1	54,68
12	1	1	-1	1	-1	66,72
13	1	1	1	-1	-1	68,00
14	1	-1	-1	-1	-1	40,06
15	1	-1	1	-1	-1	49,33
16	1	1	-1	-1	-1	66,00
17	1	+α	0	0	0	76,36
18	1	-α	0	0	0	41,00
19	1	0	+α	0	0	67,20
20	1	0	-α	0	0	53,25
21	1	0	0	+α	0	69,30
22	1	0	0	-α	0	49,38
23	1	0	0	0	+α	57,60
24	1	0	0	0	-α	57,49
25	1	0	0	0	0	68,31
26	1	0	0	0	0	67,16
27	1	0	0	0	0	66,27
28	1	0	0	0	0	72,65

Заданы:

y₃*k₁

y₉*k₂

поиск max или min

k₁=1,05;

k₂=0,5.

Цель работы:

-  рассчитать коэффициенты нелинейных уравнений регрессии с учетом и без учета двойных межфакторных взаимодействий;

-  оценить их значимость;

-  проверить адекватность полученного уравнения с учетом произведенных 4-х параллельных опытов в нулевой точке;

-  рассчитать максимум или минимум y полученного уравнения регрессии.

Ход работы:

Сначала, предположим, что уравнение регрессии является нелинейным, т.е. может быть представлено в виде:

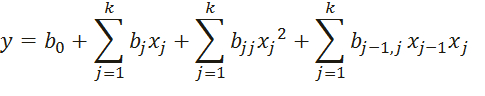
где i - номер опыта; j - номер коэффициента, k - количество факторов.

Рассчитаем количество экспериментов N, значение α и S:

=28

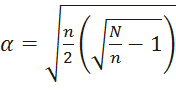= 1,607

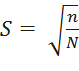= 0,756

где N - количество опытов (точка (0; 0; 0) входит);

n - количество опытов ПФЭ без точек (0; 0; 0).

Рассчитаем коэффициенты уравнения регрессии по формулам:

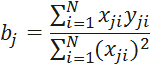
Рассчитаем дисперсию воспроизводимости:

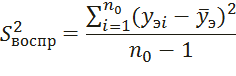
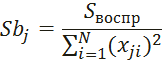
Из соотношения 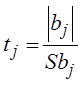, сравнивается с табличным значением при заданных значениях уравнения α (α=0,05) и числом степеней свободы (n₀-1), т.е.

Значимыми оказались следующие коэффициенты:

b₀=58,4

b₁=7,4

b₃=2,46

b₁₂=-3,48

b₃₄=2,8

b₁₁=-3,6

b₃₃=-2,77

b₄₄=-3,47

Вид уравнения до проверки коэффициентов на значимость:

y=58,4+x₁*7,4+x₂*0,9+x₃*2,5+x₄*1,2-x₁₂*3,5+x₁₃*1,6-x₁₄*1,9+x₂₃*2,1-x₂₄*1,6+x₃₄*2,8-(x₁₁-0,75)*3,6-(x₂₂-0,75)*2,4-(x₃₃-0,75)*2,77-(x₄₄-0,75)*3,47

Вид уравнения регрессии после проверки коэффициентов на значимость (с учетом двойного межфакторного взаимодействия):

y=58,4+x₁*7,4+x₃*2,5-x₁₂*3,5+x₃₄*2,8-(x₁₁-0,75)*3,6-(x₃₃-0,75)*2,77-(x₄₄-0,75)*3,47

Вид уравнения регрессии после проверки коэффициентов на значимость (без учета двойного межфакторного взаимодействия):

y=58,4+x₁*7,4+x₃*2,5

Для проверки адекватности полученного уравнения регрессии рассчитывается F-критерий Фишера.

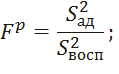
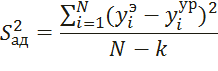
По результатам вычислений, подробно приведенных в файле exel, выяснили, что уравнение регрессии, составленное с учетом двойных межфакторных взаимодействий, является адекватным. Однако, уравнение регрессии, составленное без учета двойных межфакторных взаимодействий не является адекватным.

С помощью функции «Поиск решения» в программе Exel, нашли координаты точек max и min.

y_max= 73,867, (1,1,-1,0.56,0.23);

y_min=39,851, (1,-1,-1,-1,1).

Вывод:

Рассчитали коэффициенты нелинейных уравнений регрессии с учетом и без учета двойных межфакторных взаимодействий, оценили их значимость.

Проверили адекватность полученного уравнения с учетом произведенных 4-х параллельных опытов в нулевой точке.

Рассчитали максимум и минимум y полученного уравнения регрессии.