Математическое описание реактора с неподвижным слоем катализатора. Вектор массовой скорости, направленный вдоль оси трубки. Коэффициент эффективной диффузии в слое

7.8. Математическое описание реактора с неподвижным слоем катализатора

При строгом подходе к математическому описанию неподвижного слоя катализатора приведенные выше уравнения, выражающие процесс па зерне, должны рассматриваться совместно с уравнениями гидродинамики, описывающими движение потока в пространстве между зернами.

Ввиду очень больших трудностей, возникающих при таком подходе, используется квазигомогенная модель зернистого слоя, аналогичная квазигомогенной модели зерна катализатора. Эта модель заключается в следующем:

1.  Слой рассматривают как однородную среду с непрерывным распределением концентраций и температур.

2.  Скорости реакций усредняют по объему слоя. Переход от средней скорости -ой реакции в зерне  к скорости, рассчитанной на единицу объема слоя , производят по соотношению

,                                                             (7.58)

где  - доля свободного объема (пористость) слоя.

3.  Перенос тепла и вещества в слое характеризуют эффективными коэффициентами теплопроводности и диффузии, которые зависят от физических свойств смеси, скорости движения, размеров и формы зерен и структуры зернистого слоя.

Применение квазигомогенной модели обосновано при условии, что участки слоя катализатора, в пределах которых изменения температуры и концентрации малы по сравнению с их средним значением, содержат достаточно большое число зерен. При этом сами участки могут быть значительно меньше размеров всего слоя.

Показано, что в промышленных реакторах с неподвижным слоем катализатора, где длина слоя много больше диаметра зерна катализатора, осевой перенос вещества и тепла в результате эффективной диффузии и теплопроводности в отличие от конвективного переноса очень мал и, как правило, может не учитываться.

Радиальный перенос тепла и вещества в адиабатических реакторах отсутствует, однако при наличии теплоотвода он происходит. Рассмотрим материальный баланс элементарного объема зернистого слоя по -му компоненту.

Количество -гo компонента, уходящего через поверхность выделенного объема в результате эффективной диффузии в единицу времени

,                                                где  - вектор массовой скорости, направленный вдоль оси трубки;  - осевая координата.

Количество -гo компонента, уходящего через поверхность выделенного объема в результате эффективной диффузии в единицу времени

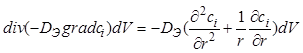,                           где  - коэффициент эффективной диффузии в слое (поскольку диффузионный перенос имеет гидродинамическую природу, то коэффициенты эффективной диффузии различных компонентов не отличаются друг от друга);  - радиальная координата.

Здесь учтена осесимметричность цилиндрического слоя и опущены члены, содержащие производную по , поскольку, как сказано выше, осевой перенос можно не учитывать.

Количество -гo компонента, образующееся в объеме  в единицу времени, составляет

.                                                              

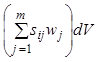Приравнивая в стационарном состоянии приход и уход, получим уравнение:

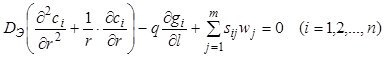,      (7.59)

Тепловой баланс элементарного объема приводит к аналогичному уравнению

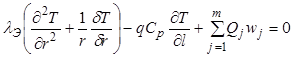,                             (7.60)

где  - эффективная теплопроводность слоя.

Граничные условия:

а)   На наружной поверхности слоя катализатора радиальный поток вещества

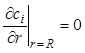,                                                                  (7.61)

а радиальный поток тепла равен теплу, отводимому от слоя охлаждающей средой:

,                                                (7.62)

где  - наружный радиус слоя катализатора;  - коэффициент теплопередачи от слоя к охлаждающей среде.

б)   На оси слоя выполняются условия симметрии

,       ,                                          (7.63)

.                                                                   (7.64)

Обычно в реакторах допускаются относительно небольшие радиальные перепады температуры и концентраций, поскольку значительная поперечная неравномерность неблагоприятно влияет на ход процесса. Поэтому, выбрав при помощи уравнений (7.59), (7.30) диаметр трубки, обеспечивающий допустимую степень радиальной неравномерности, можно во всех дальнейших расчетах ее не учитывать. Это значит, что радиальный перенос тепла и вещества эффективной диффузией и теплопроводностью не рассматривается, а концентрации и температура принимаются постоянными вдоль радиуса. Отсюда можно сделать вывод, что для реактора с неподвижным слоем катализатора в указанных условиях применима квазигомогенная модель и аппарат работает в режиме идеального вытеснения.

Уравнения материального и теплового баланса «квазигомогенного»