В связи с трудностями, имеющимися при построении математических моделей ректификационных колонн из-за недостаточной разработки вопросов теории массопереноса в многокомпонентных многофазных системах, рассмотрим только некоторые распространенные модели.
· Модель 7 построена на концепции теоретической ступени разделения. Основные допущения, приводящие к этой модели, следующие:
1) паровая фаза, покидающая ступень разделения, находится в равновесии с жидкой фазой;
2) в паровой и жидкой фазах принято идеальное перемешивание;
3) унос жидкости отсутствует.
Математическое описание для этой модели содержит следующие уравнения:
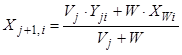 ,
, ![]() , (8.59)
, (8.59)
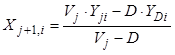 ,
, ![]() , (8.60)
, (8.60)
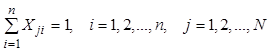 , (8.61)
, (8.61)
![]() , (8.62)
, (8.62)
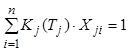 , (8.63)
, (8.63)
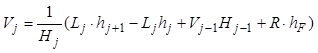 , (8.64)
, (8.64)
где
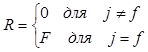 , (8.65)
, (8.65)
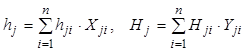 , (8.66)
, (8.66)
(здесь ![]() ,)
,)
![]() , (8.67)
, (8.67)
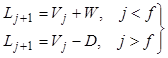 . (8.68)
. (8.68)
Уравнения (8.59) и (8.60) описывают покомпонентный материальный баланс. Уравнение (8.61) служит для расчета равновесного состава пара идеальных смесей. Зависимости энтальпий и константы фазового равновесия от температуры аппроксимируются уравнениями (8.67).
Модель 8 принимается при следующих допущениях:
1) жидкая фаза идеально перемешана;
2) в паровой фазе полное вытеснение в зоне массообмена и идеальное перемешивание в межтарелочном пространстве;
3) давление в колонне постоянно;
4) унос жидкости отсутствует;
5) тарелка работает в адиабатическом режиме;
6) массопередача в зоне массообмена эквимолярная;
7) кинетические зависимости могут быть представлены в форме, приведенной в работе.
Уравнения модели имеют следующий вид:
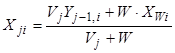 ,
, 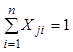 ,
,
![]() , (8.69)
, (8.69)
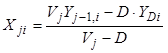 ,
, ![]() , (8.70)
, (8.70)
![]() , (8.71)
, (8.71)
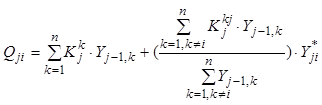 , (8.72)
, (8.72)
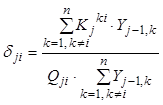 , (8.73)
, (8.73)
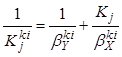 , (8.74)
, (8.74)
![]() , (8.75)
, (8.75)
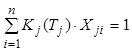 , (8.76)
, (8.76)
![]() , (8.77)
, (8.77)
![]() . (8.78)
. (8.78)
Уравнение (8.71) учитывает кинетику массопередачи в многокомпонентной системе, вывод уравнения можно найти в работах.
Модель 9 применяется в случаях моделирования статического режима ректификационной колонны с отбором бокового погона при допущениях, принятых в модели 7.
Уравнения, описывающие модель 9, имеют вид
![]()
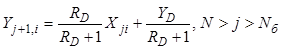 , (8.79)
, (8.79)
где ![]() - флегмовое число, представляющее
отношение расхода жидкости, стекающей с верхних тарелок, к дистилляту
- флегмовое число, представляющее
отношение расхода жидкости, стекающей с верхних тарелок, к дистилляту ![]() ;
; ![]() -
номер тарелки отбора бокового погона.
-
номер тарелки отбора бокового погона.
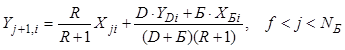 , (8.80)
, (8.80)
где ![]() -
флегмовое число, равное отношению расхода жидкости в рассчитываемой секции к
суммарной величине дистиллята и бокового погона.
-
флегмовое число, равное отношению расхода жидкости в рассчитываемой секции к
суммарной величине дистиллята и бокового погона.
Уравнения для расчета составов равновесных фаз и уравнения концентраций для отгонной секции колонны остаются такими же, как и соответствующие уравнения для расчета колонны без бокового отбора, а именно:
1) уравнение для расчета состава равновесной жидкости (укрепляющая секция)
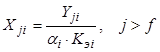 , (8.81)
, (8.81)
где
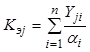 ; (8.82)
; (8.82)
2) уравнение для расчета состава равновесных паров (отгонная секция)
![]() , (8.83)
, (8.83)
где
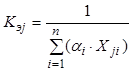 ; (8.84)
; (8.84)
3) уравнение концентраций для отгонной секции
![]() , (8.85)
, (8.85)
где ![]() -
паровое число.
-
паровое число.
Для расчета начального приближения применяются уравнения, отвечающие режиму полного орошения:
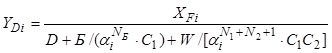 , (8.86)
, (8.86)
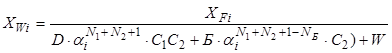 . (8.87)
. (8.87)
Величины ![]() и
и
![]() находятся путем решения системы
двух нелинейных уравнений (8.86) и (8.87), исходя из условий:
находятся путем решения системы
двух нелинейных уравнений (8.86) и (8.87), исходя из условий:
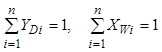 . (8.88)
. (8.88)
Для ускорения сходимости расчета применяется уравнение, полученное в результате совместного решения уравнений:
![]() (8.89)
(8.89)
и
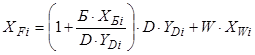 .
(8.90)
.
(8.90)
где ![]() -
корректирующий множитель, учитывающий невязки при итерационном расчете составов
дистиллята и остатка.
-
корректирующий множитель, учитывающий невязки при итерационном расчете составов
дистиллята и остатка.
Окончательное решение системы уравнений (8.86)-(8.87) позволяет получить уравнение вида
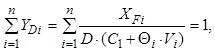 (8.91)
(8.91)
где
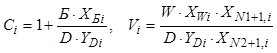 . (8.92)
. (8.92)
Для однозначного решения уравнения (8.91)
принимается, что ![]() для ведущего компонента.
По величине
для ведущего компонента.
По величине ![]() корректируются составы дистиллята
и остатка по следующим уравнениям:
корректируются составы дистиллята
и остатка по следующим уравнениям:
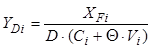 , (8.93)
, (8.93)
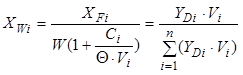 .
(8.94)
.
(8.94)
Расчет заканчивается при достижении заданной
точности по величине ![]() , которая стремится к
единице.
, которая стремится к
единице.
Модель 10 применяется при расчете сложных тарельчатых ректификационных колонн, предназначенных для разделения как идеальных, так и неидеальных многокомпонентных смесей. Она также может быть использована для моделирования динамических режимов ректификационных колонн. Для этой модели принижаются следующие допущения:
1) паровая фаза, покидающая тарелку, находится в равновесии с жидкой фазой;
2) жидкая фаза идеально перемешивается;
3)
давление в колонке ![]() постоянно;
постоянно;
4) не учитывается тепловое взаимодействие потоков.
Структурную схему для этой модели можно рассматривать как дискретную последовательность стадий смешения потоков, поступающих на тарелку, однократного испарения и разделения смеси на равновесные потоки, как показано на рис. 8.3.
Математическое описание модели 10 включает следующие уравнения.
Исходя из условия идеального
перемешивания приходящих потоков на ![]() -ую ступень
разделения, можно записать уравнение дня определения состава смеси в следующем
виде:
-ую ступень
разделения, можно записать уравнение дня определения состава смеси в следующем
виде:
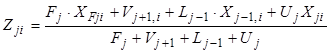 , (8.95)
, (8.95)
где ![]() -
параметр, учитывающий изменение удерживающей способности
-
параметр, учитывающий изменение удерживающей способности ![]() -ой тарелки по жидкости в единицу
времени,
-ой тарелки по жидкости в единицу
времени, ![]() - состав смеси на тарелке.
- состав смеси на тарелке.
Значение ![]() при
расчете статического режима можно принять равным нулю, так как составы
продуктов, отвечающие стационарному состоянию колонны, не зависят от начальных
условий и удерживающей способности тарелки.
при
расчете статического режима можно принять равным нулю, так как составы
продуктов, отвечающие стационарному состоянию колонны, не зависят от начальных
условий и удерживающей способности тарелки.
Для определения температуры на ![]() -ой ступени разделения используется
-ой ступени разделения используется
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.