массопередача по фазам независима, диффузионные сопротивления аддитивны, т.е. общий коэффициент массопередачи может быть разложен на частные;
5) коэффициенты массоотдачи постоянны по поверхности контактного устройства;
6) унос жидкости постоянен.
Математическое описание модели 2 включает систему уравнений (8.1)-(8.6) и дополняется следующими уравнениями:
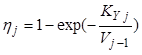 , (8.8)
, (8.8)
где
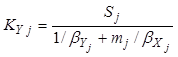 , (8.9)
, (8.9)
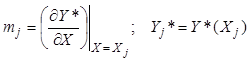 , (8.10)
, (8.10)
![]() , (8.11)
, (8.11)
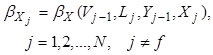 . (8.12)
. (8.12)
Здесь ![]() -
коэффициент массопередачи;
-
коэффициент массопередачи; ![]() и
и ![]() - частные коэффициенты
массоотдачи по паровой и жидкой фазе соответственно;
- частные коэффициенты
массоотдачи по паровой и жидкой фазе соответственно; ![]() - эффективная площадь тарелки.
- эффективная площадь тарелки.
Конкретный вид уравнений (8.11) и
(8.12) зависит от конструктивных особенностей тарелки и физико-химических
свойств разделяемых компонентов. Данная модель имеет минимум два настроечных
параметра ![]() и
и ![]() .
.
· Модель 3 принимается при следующих допущениях:
1) жидкая и паровая фазы идеально перемешаны;
2)
равновесная кривая имеет
линейный характер в пределах измерения концентрации ![]() на
на
![]() -том контактном устройстве;
-том контактном устройстве;
3) унос жидкости отсутствует;
4) выполняются допущения 1 и 4-5, принятые для модели 2.
Уравнения, описывающие модель 3, имеют вид
![]() , (8.13)
, (8.13)
![]() , (8.14)
, (8.14)
![]() , (8.15)
, (8.15)
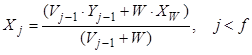 , (8.16)
, (8.16)
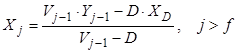 , (8.17)
, (8.17)
![]() , (8.18)
, (8.18)
где
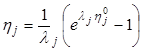 , (8.19)
, (8.19)
локальный КПД
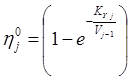 , (8.20)
, (8.20)
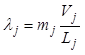 ,
, 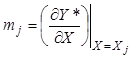 , (8.21)
, (8.21)
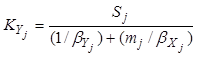 , (8.22)
, (8.22)
![]() , (8.23)
, (8.23)
![]() . (8.24)
. (8.24)
Эта модель также имеет два настроечных
параметра ![]() и
и ![]() .
.
· Модель 4 принимается при следующих допущениях:
1) гидродинамическая обстановка в жидкой и паровой фазах может быть представлена в виде однопараметрической диффузионной модели;
2) коэффициенты перемешивания постоянны;
3)
кривая равновесия линейна в
пределах изменения концентрации ![]() на контактном
устройстве;
на контактном
устройстве;
4) унос жидкости отсутствует;
5) выполняются допущения 1 и 4-5, принятые для модели 2.
Математическое описание модели 4 включает систему уравнений (8.13)-(8.17), (8.22)-(8.24) и дополняется следующими уравнениями:
![]() , (8.25)
, (8.25)
где
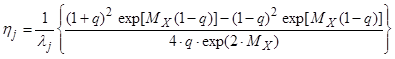 , (8.26)
, (8.26)
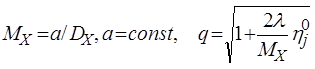 , (8.27)
, (8.27)
![]() ,
, 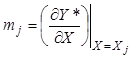 , (8.28)
, (8.28)
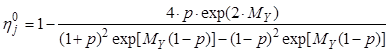 , (8.29)
, (8.29)
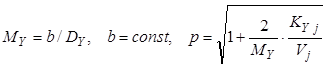 , (8.30)
, (8.30)
![]() ,
, ![]() . (8.31)
. (8.31)
Для этой модели можно выделить не менее
четырех параметров настройки: ![]() ,
, ![]() ,
, ![]() ,
,
![]() , которые могут иметь следующие
частные случаи при использовании модели 4:
, которые могут иметь следующие
частные случаи при использовании модели 4:
1)
при ![]() (
(![]() ) перемешивание в паровой фазе
отсутствует и принимается модель идеального вытеснения, - тогда
) перемешивание в паровой фазе
отсутствует и принимается модель идеального вытеснения, - тогда 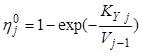 ;
;
2)
при ![]() (
(![]() )
в паровой фазе принимается полное перемешивание, - тогда
)
в паровой фазе принимается полное перемешивание, - тогда 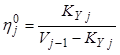 ;
;
3)
при ![]() ,
, ![]() случай
сводится к модели 3;
случай
сводится к модели 3;
4)
при ![]() ,
,
![]() случай сводится к модели 2;
случай сводится к модели 2;
5)
при ![]() ,
,
![]() получаем
получаем ![]() , т.е. частный случай модели 1.
, т.е. частный случай модели 1.
· Модель 5 принимается при следующих допущениях:
1) по жидкой фазе приняла ячеечная модель;
2) по паровой фазе принята модель идеального вытеснения;
3) равновесная кривая линейна в пределах изменения концентрации на контактном устройстве;
4) локальный кпд постоянен по всей площади контактного устройства;
5) объёмы ячеек и время пребывания в них равны между собой;
6) унос жидкости отсутствует;
7) выполняются допущения 1 и 4-5, принятые для модели 2.
Математическое описание модели 5 включает систему уравнений (8.13)-(8.17) и дополняется следующими уравнениями:
![]() , (8.32)
, (8.32)
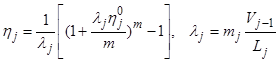 , (8.33)
, (8.33)
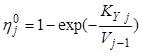 . (8.34)
. (8.34)
Здесь ![]() -
число ячеек, на которые разбивается эффективная площадь тарелки.
-
число ячеек, на которые разбивается эффективная площадь тарелки.
Модель 5 имеет три параметра настройки ![]() ,
, ![]() и
и
![]() .
.
· Модель 6 принимается при следующих допущениях:
1) теплоты смешения потоков жидкости пренебрежимо малы;
2) режим работы контактного устройства - адиабатический;
3) выполняется допущения 2-5, принятые для модели 2.
Математическое описание модели 6 имеет следующий вид
![]() , (8.35)
, (8.35)
![]() , (8.36)
, (8.36)
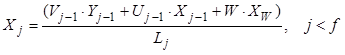 , (8.37)
, (8.37)
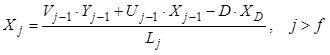 , (8.38)
, (8.38)
![]() , (8.39)
, (8.39)
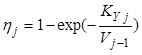 ,
, 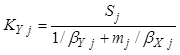 , (8.40)
, (8.40)
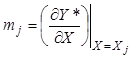 , (8.41)
, (8.41)
![]() , (8.42)
, (8.42)
![]() , (8.43)
, (8.43)
![]() , (8.43)
, (8.43)
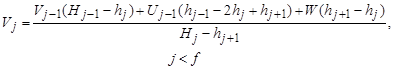 , (8.44)
, (8.44)
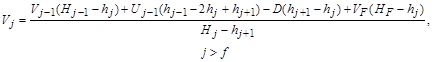 , (8.45)
, (8.45)
![]() , (8.46)
, (8.46)
![]() , (8.47)
, (8.47)
![]() ,
, ![]() , (8.48)
, (8.48)
![]() . (8.49)
. (8.49)
Величина уноса U (8.43) зависит от конструктивных особенностей контактного устройства,
физико-химических свойств компонентов и может быть определена по уравнениям,
приведенным, например, в работе. Уравнения (8.46)-(8.49) обычно
представляют в виде полиномов, удобных для реализации на ЭВМ. Данная модель
имеет три настроечных параметра ![]() ,
, ![]() ,
, ![]() .
.
Уравнение, описывающее систему дефлегматор - конденсатор - емкость, может быть представлено в виде:
![]() , (8.50)
, (8.50)
где ![]() -
эффективность дефлегматора,
-
эффективность дефлегматора, ![]() .
.
Возможны частные случаи:
1)
![]() , что справедливо для полного конденсатора,
, что справедливо для полного конденсатора, ![]() ;
;
2)
![]() , что справедливо для парциального конденсатора, тогда
, что справедливо для парциального конденсатора, тогда ![]() , т.е. существует дополнительное
разделение.
, т.е. существует дополнительное
разделение.
Часто при моделировании процесса ректификации на ЭВМ в качестве парциального конденсатора принимают одну теоретическую ступень разделения.
В простейшем случае уравнение, описывающее кипятильник, монет быть представлено в виде
![]() , (8.51)
, (8.51)
где ![]() -
эффективность кипятильника,
-
эффективность кипятильника, ![]() .
.
Частные случаи:
1)
![]() , что обычно справедливо для полного кипятильника (испарителя),
тогда
, что обычно справедливо для полного кипятильника (испарителя),
тогда ![]() ;
;
2)
![]() , что справедливо для парциального кипятильника (испарителя).
, что справедливо для парциального кипятильника (испарителя).
Количество тепла, вносимое в кипятильник колонны с паровым потоком, может быть записано в общем виде:
![]() . (8.52)
. (8.52)
Приведенные выше системы уравнений
устанавливают соотношение между концентрациями легколетучего компонента в фазах
по высоте колонны ![]() ,
, ![]() и режимными (входными)
переменными:
и режимными (входными)
переменными: ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() . В нее входят нелинейные уравнения и, следовательно, колонна является
нелинейным объектом. Количество уравнений в системе меньше числа переменных,
входящих в эти уравнения, на 5 и, следовательно, система является
неопределенной. Она будет определена после задания величин каких-либо пяти переменных.
. В нее входят нелинейные уравнения и, следовательно, колонна является
нелинейным объектом. Количество уравнений в системе меньше числа переменных,
входящих в эти уравнения, на 5 и, следовательно, система является
неопределенной. Она будет определена после задания величин каких-либо пяти переменных.
В соответствии с физическим смыслом работы колонны этим пятью
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.