Перейдем к математическому описанию последовательности реакторов или, другими словами, многоступенчатого реактора.
Реактор состоит из ряда ступеней (стадий, секций), в которых происходят химические превращения, и расположенных между ними физических аппаратов (теплообменников и смесителей), в которых меняются некоторые параметры реакционного потока. Рассмотрим отдельно ступени и промежуточные аппараты.
Ступень представляет собой химический реактор, математическое описание которого было дано выше. Здесь приведем общую структуру уравнений химического реактора, являющегося ступенью многоступенчатого реактора.
Обозначим число
ступеней через ![]() , и будем отсчитывать
время контакта от начала первой ступени. Обозначим также время контакта в конце
, и будем отсчитывать
время контакта от начала первой ступени. Обозначим также время контакта в конце![]() -ой ступени и начале
-ой ступени и начале ![]() -ой ступени через
-ой ступени через ![]() . Время контакта
. Время контакта ![]() -ой ступени равно
-ой ступени равно ![]() . В начале первой ступени
. В начале первой ступени ![]() t0.
t0.
Для удобства
записи параметры реакционного потока внутри ![]() -ой
ступени (концентрации и температуру) обозначим через
-ой
ступени (концентрации и температуру) обозначим через![]() ,
где
,
где ![]() - номер переменной,
- номер переменной, ![]() - номер ступени, причем первые
- номер ступени, причем первые ![]() переменных
переменных ![]() будут представлять собой
концентрации, а
будут представлять собой
концентрации, а ![]() температуру. Значения
переменных на входе в
температуру. Значения
переменных на входе в ![]() -ую ступень и выходе из
нее обозначим соответственно через
-ую ступень и выходе из
нее обозначим соответственно через ![]() и
и ![]() . Для реакторов всех типов за
исключением реактора полного смешения параметры реакционной смеси меняются по
длине реактора
. Для реакторов всех типов за
исключением реактора полного смешения параметры реакционной смеси меняются по
длине реактора
![]() ,
, ![]() , причем
, причем
![]() ,
, ![]() .
.
Для реактора
полного смешения ![]() .
Обозначим еще через
.
Обозначим еще через ![]() параметры, входящие в
правые части уравнений (7.42) и (7.45). К ним относятся параметры потока
хладоагента (температура, давление, состав), конструкционные параметры
параметры, входящие в
правые части уравнений (7.42) и (7.45). К ним относятся параметры потока
хладоагента (температура, давление, состав), конструкционные параметры ![]() -ой ступени и т.д. Внутри
интервала
-ой ступени и т.д. Внутри
интервала ![]() величина
величина ![]() не зависит от времени контакта
не зависит от времени контакта ![]() .
.
Переменные ![]() будем называть в дальнейшем
фазовыми переменными, а параметры
будем называть в дальнейшем
фазовыми переменными, а параметры ![]() управляющими
переменными. Примем для простоты, что изменения давления реакционной смеси и
температуры хладоагента по длине ступени можно не учитывать.
управляющими
переменными. Примем для простоты, что изменения давления реакционной смеси и
температуры хладоагента по длине ступени можно не учитывать.
Пусть
рассматривается последовательность реакторов идеального вытеснения, работающих
стационарно. В новых обозначениях уравнения, описывающие изменение параметров
процесса в ![]() -ой ступени, имеют вид
обыкновенных дифференциальных уравнений:
-ой ступени, имеют вид
обыкновенных дифференциальных уравнений:
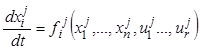 , (7.85)
, (7.85)
![]() ,
, ![]() ,
, ![]() .
.
Разберем теперь
ступень, представляющую собой каталитический реактор, работающий в квазистатическом
режиме. Параметры газового потока будем по-прежнему обозначать через ![]() , а переменные, характеризующие
состояние катализатора, - как
, а переменные, характеризующие
состояние катализатора, - как ![]() . Тогда
уравнения, описывающие процессы в
. Тогда
уравнения, описывающие процессы в ![]() -ой секции,
примут форму дифференциальных уравнений в частных производных:
-ой секции,
примут форму дифференциальных уравнений в частных производных:
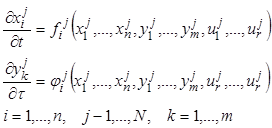 . (7.86)
. (7.86)
Наконец, если секции являются реакторами, полного смешения, то они описываются конечными уравнениями:
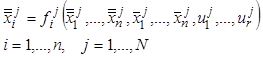 . (7.87)
. (7.87)
Этими уравнениями
задается неявная зависимость выходных значений параметров ![]() от входных
от входных ![]() . Примем, что их можно решить
относительно
. Примем, что их можно решить
относительно ![]() , т.е. зависимость
выходных значений параметров от входных может быть выражена в явной форме
(обозначение функциональной зависимости не меняется):
, т.е. зависимость
выходных значений параметров от входных может быть выражена в явной форме
(обозначение функциональной зависимости не меняется):
![]() . (7.88)
. (7.88)
Уравнения,
описывающие промежуточные аппараты, дают соотношения, связывающие входные и выходные
значения переменных двух последовательных ступеней, т.е. ![]() и
и ![]() ,
,
![]() Эти соотношения, естественно, зависят от вида промежуточного аппарата
Эти соотношения, естественно, зависят от вида промежуточного аппарата
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.