Типовые математические модели структуры потоков в аппаратах. Модель идеального вытеснения и её характеристика. Диффузионные модели

4. Типовые математические модели структуры потоков в аппаратах

Все многообразие математических моделей потоков, возникающих в различных аппаратах, может быть представлено в зависимости от вида функции распределения.

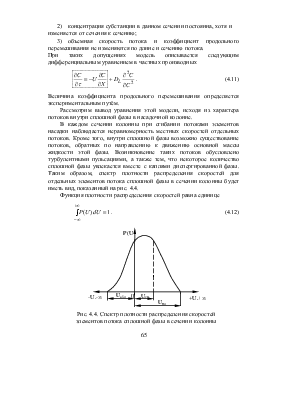
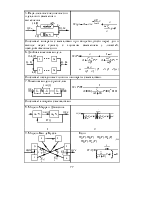
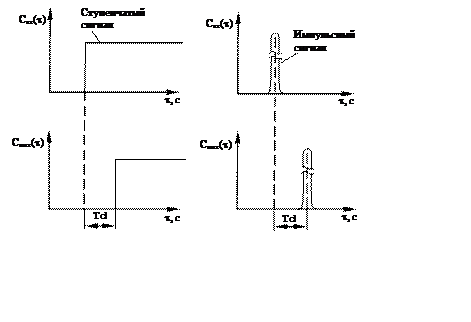
Чтобы установить вид функции распределения любого процесса химической технологии, необходим эксперимент с подачей сигнала (индикатора) на вход системы в виде ступенчатого, импульсного или частотного возмущения. При ступенчатом возмущении изменяют входную величину (например, концентрацию индикатора) до нового значения скачком и получают так называемую кривую разгона по выходной координате. При импульсном возмущении изменяют входную величину мгновенно (дельта-функция), а при частотном возмущении входную величину изменяют по закону гармонического колебания (синусоидальное возмущение). На рис. 4.1 показаны три вида входных и выходных сигналов.

В зависимости от вида кривой разгона определяют передаточную функцию и принадлежность характеристики исследуемого объекта к одному из типов математической модели структуры потоков в аппарате.

4.1. Модель идеального вытеснения и её характеристика

Для этой модели принимается поршневое течение без перемешивания в направлении, перпендикулярном движению. Время пребывания в системе всех частиц одинаково и равно отношению объема системы  к объемному расходу , т.е. . Математическое описание модели имеет вид

,                                                                               (4.1)

где  - концентрация субстанции (вещества или энергии),  - время,  - линейная скорость потока,  - координата.

Модели идеального вытеснения, в первом приближении, соответствуют процессы, происходящие в трубчатых аппаратах при отношении длины трубы к диаметру более 20.

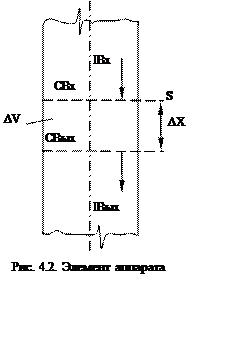
На рис. 4.2 показан элемент аппарата и изображены следующие условные обозначения: ,  - концентрации субстанции в сечениях на границе элементарного объема  на элементарном участке ,  - поток, входящий в элементарный объем,  - поток на выходе из элементарного объема,  - сечение аппарата,  - линейная скорость потока. Рассмотрим вывод уравнения модели идеального вытеснения.

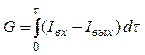,                                                   (4.2)

где

,                      .                               (4.3)

Подставив выражения (4.3) в уравнение (4.2), получим

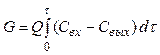.                                                              (4.4)

Поделим обе части уравнения (4.4) на

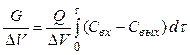.                                                       (4.5)

Отношение  есть изменение концентрации субстанции в пределах элементарного объема с поперечным сечением, равным единице, и высотой . Поэтому можно записать

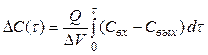.                                                  (4.6)

Учитывая, что  и , получим

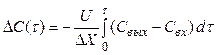.                                                (4.7)

Разделим переменные и продифференцируем уравнение (4.7)

.                                         (4.8)

Переходя от полного дифференциала к частному с учетом условия квазистационарности, получим

.                                                                               (4.9)

Эта модель относится к модели с распределенными параметрами, в которой изменение концентрации является непрерывной функцией во времени и координаты .

Модель идеального вытеснения характеризуется функциями отклика, приведенными на рис. 4.3.

Передаточная функция модели идеального вытеснения имеет следующий вид:

,                                                                                   (4.10)

где  - транспортное запаздывание аппарата,  - длина аппарата,  - линейная скорость потока.

4.2. Диффузионные модели

Различают две разновидности диффузионных моделей: однопараметрическую и двухпараметрическую.

Однопараметрическая диффузионная модель представляет собой модель идеального вытеснения, осложненную обратным перевешиванием, подчиняющимся формальному закону диффузии. Дополнительным параметром, характеризующим эту модель, служит коэффициент турбулентной диффузии или коэффициент продольного перемешивания .

При составлении однопараметрической диффузионной модели принимаются следующие допущения:

1)  изменение концентрации субстанции является непрерывной функцией координаты (длины, высоты);

2)  концентрация субстанции в данном сечении постоянна, хотя и изменяется от сечения к сечению;

3)  объемная скорость потока и коэффициент продольного перемешивания не изменяются по длине и сечению потока.

При таких допущениях модель описывается следующим дифференциальным уравнением в частных производных

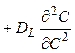.                                                           (4.11)

Величина коэффициента продольного перемешивания определяется экспериментальным путём.

Рассмотрим вывод уравнения этой модели, исходя из характера потоков внутри сплошной фазы в насадочной колонне.

В каждом сечении колонны при сгибании потоками элементов насадки