Изложенная выше процедура расчета сушилки псевдоожиженного слоя основана на двух допущениях: 1) температура слоя постоянна; 2) осушающий газ является однородным, т.е. газ в псевдоожиженном слое не разделяется на ожижающий газ и фазу газовых пузырей. Хотя при определенных условиях эти допущения и являются справедливыми, во многих случаях необходима модель, отражающая реальную структуру псевдоожиженного слоя.
Рассмотрим физическую картину процесса псевдоожижения. Псевдоожиженным называется слой, в котором легкие твердые частицы приходят в состояние, подобное жидкому, вследствие контакта с газом. При низких скоростях поток газа просто фильтруется через пустоты между частицами; в таком состоянии они составляют неподвижный слой. С увеличением скорости потока частицы будут двигаться друг относительно друга и совершать колебательные движения с малыми амплитудами; в таком состоянии частицы образуют так называемый расширенный слой. При более высокой скорости потока достигается состояние, когда почти все частицы составляют нечто вроде суспензии с текущим вверх потоком газа, В этой области трение между частицей и потоком компенсируется весом частицы. Такое состояние слоя называется состоянием минимального псевдоожижения. При дальнейшем увеличении скорости потока начинают появляться неоднородности в виде пузырей газа, проходящих через слой без взаимодействия с частицами. Этот слой обычно и называется псевдоожженным. Следует отметить, что между газовыми пузырями и плотной фазой происходит газовый обмен. При движении мелких пузырей газ, фильтрующийся через плотную фазу, движется вверх быстрее пузыря; следовательно, прохождение газа в пузыре представляет для газа путь наименьшего сопротивления. Газ входит в нижнюю часть пузыря, а выходит из верхней. Часть газа в виде кольцевой пленки перемещается вместе с пузырем. Скорость движения крупных пузырей больше скорости движения газа в плотной фазе, Поэтому при их движении газовый поток входит в пузырь у основания, покидает его у свода и, огибая пузырь, снова поступает в его нижнюю часть. Зона вокруг пузыря, пронизываемая циркулирующими струями газа, называется облаком.
Движение газа в псевдоожиженном слое может быть описано с помощью двухфазной модели, согласно которой слой представляется состоящим из двух фаз: фазы пузырей и плотной фазы (которая включает частицы и ожижающий газ и сохраняется при минимальной скорости сжижения). При этом избыточный поток сжижающего газа по отношению к минимальному сжижающему потоку проходит через слой в виде пузырей (рис. 11.2). Для дальнейшего вывода модели сделаем следующие допущения: 1) фаза пузырей, ожижающий газ и твердые частицы считаются непрерывными; 2) фаза пузырей свободна от твердых частиц и размер пузырей одинаков;
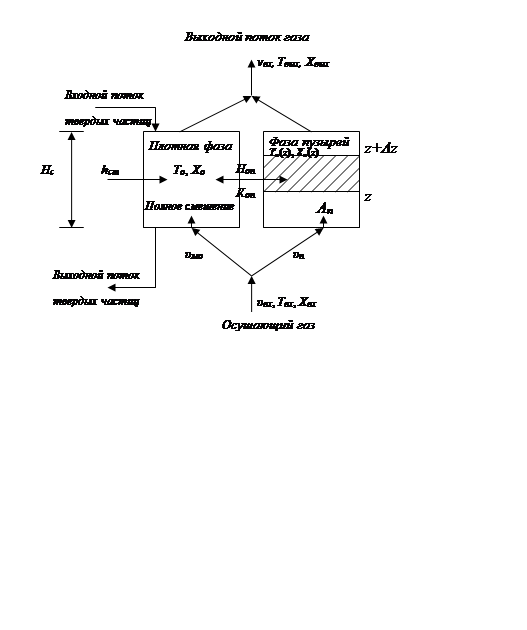Рис. 11.2. Схематическое представление структуры псевдоожиженного слоя
в сушилке: 
- высота псевдоожиженного слоя; 
- скорость газа в слое; 
- температура газа на входе; 
- влагосодержание газа на входе; 
, 
-
температура и влагосодержание плотной фазы; 
,
- температура и влагосодержание в
фазе пузырей; 
- вертикальная
координата; 
- объемный коэффициент
теплопередачи между фазой пузырей и плотной фазой; 
-
коэффициент газового обмена между фазой пузырей и плотной фазой, отнесенный к
единице объема пузырей
3) пузыри газа обмениваются массой и энергией только со сжижающим газом; 4) ожижающий газ и твердые частицы полностью перемешаны; 5) твердые частицы подаются и удаляются с постоянной скоростью; 5) внутреннее сопротивление твердых частиц массо- и теплопередаче пренебрежимо мало; 7) частицы имеют одинаковый размер; 8) температура и влагосодержание каждой частицы зависят от ее времени пребывания в сушилке.
При сделанных допущениях распределение времени пребывания частиц в сушилке определяется выражением
. (11.56)
Запишем теперь уравнения сохранения массы для каждой из фаз псевдоожиженного слоя в сушилке.
Рассмотрим сначала фазу пузырей.
Баланс влаги для выделенного элемента фазы высотой 
(рис.
11.2) приводит к уравнению
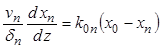(11.57)
со следующим граничным условием:
. (11.58)
Здесь 
-
скорость фазы пузырей, отнесенная ко всей площади псевдоожиженного слоя;
- доля псевдоожиженного
слоя, занимаемая фазой пузырей.
После интегрирования уравнения (11.57) получаем
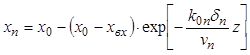. (11.59)
Параметры,
входящие в уравнение (11.59), оцениваются из следующих соотношений. Объемная
доля фазы пузырей определяется скоростью газа в слое ,
скоростью газа при минимальном псевдоожижении 
и
скоростью движения единичного пузыря 
и выражается формулой
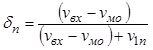, (11.60)
где
, (11.61)
- скорость газа при минимальном псевдоожижении, определяемая
соотношением
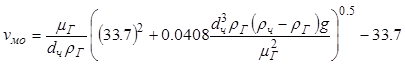, (11.62)
- диаметр пузыря
газа; 
- диаметр твердых частиц; 
, 
-
соответственно плотность влажных частиц и газа; 
-
вязкость газа. Скорость газа в фазе пузырей выражается
формулой
. (11.63)
Коэффициент газового обмена 
между фазой пузырей и плотной фазой
определяется соотношением
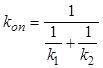, (11.64)
где 
-
коэффициент газового обмена между фазой пузырей и облаком:
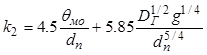, (11.65)
-
коэффициент газового обмена между облаком и плотной фазой:
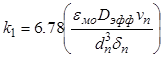, (11.66)
. (11.67)
Фаза
пузырей
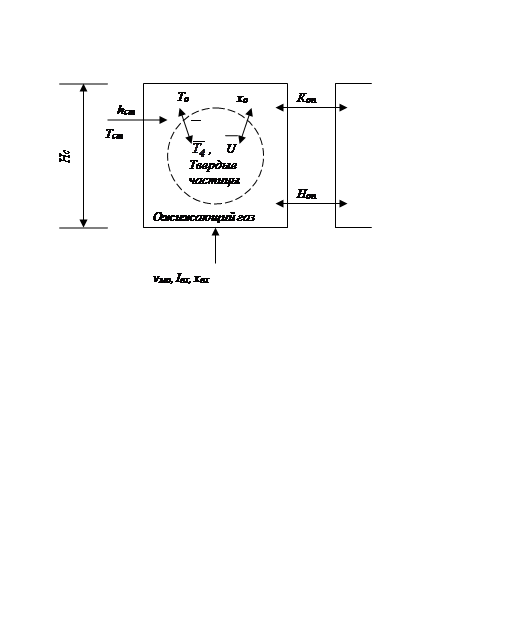Рис. 11.3. Схема
переноса массы и энергии между твердыми частицами и сжижающим газом
В уравнениях (11.65)-(11.67) 
- коэффициент молекулярной диффузии
в газе; 
- эффективный коэффициент
молекулярной диффузии в газе; 
- доля
свободного объема при минимальном псевдоожижении, равная
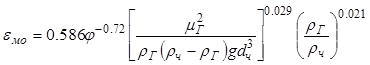; (11.68)
- фактор формы частиц.
Рассмотрим теперь уравнение сохранения массы для ожижающего газа. Из баланса влаги для ожижающего газа (рис. 11.3) получаем
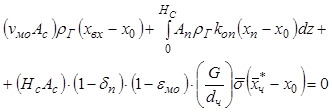, (11.69)
где 
-
среднее влагосодержание газа у поверхности частиц; 
-
коэффициент испарения.
Если обозначить среднее влагосодержание пузырей газа через
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
