Прямая на плоскости. Виды уравнения прямой на плоскости. Уравнение прямой проходящей через заданную точку перпендикулярную заданному вектору

Глава4 Прямая на плоскости.

4.1 Виды уравнения прямой на плоскости.

Некоторые виды уравнения прямой на плоскости вам уже известны из средней школы.  Здесь мы рассмотрим различные уравнения прямой на плоскости.

4.1.1Уравнение прямой проходящей через заданную точку перпендикулярную заданному вектору.

Дана точка М₀(х₀,у₀) и вектор

.

                                  у                                             

                                                                  М

 

М₀(х₀,у₀)

0

                                                                                        х

Рис 4.1

Возьмём на прямой произвольную точку М(х,у)

Рассмотрим вектор  , так как вектор , то их скалярное произведение равно нулю

Используя форму скалярного произведения для векторов заданных своими проекциями получим:

А(х-х₀)+В(у-у₀)=0

4.1.2 Общее уравнение прямой на плоскости

Ах+Ву+С=0

А,В,С – константы причём коэффициенты А и В одновременно не равны нулю.

Из общего уравнения прямой можно получить различные частные случаи в зависимости от значения коэффициентов уравнения:

а)

имеет уравнение Ах+Ву=0

эта прямая проходит через начало координат    б)

прямая параллельна оси ОХ   в)

прямая параллельна оси ОУ

4.1.3 Уравнение прямой проходящей через заданную точку параллельно заданному вектору.

Пусть задана точка М₀(х₀,у₀) и вектор

                      у

 

                                                                              М(х,у)

0

                                                    М₀(х₀,у₀)                        

                                                                                               х

Рис 4.2

Рассмотрим на прямой произвольную точку М(х,у) и найдём координаты вектора , векторы  и  параллельны по условию тогда, используя  условие параллельности двух векторов, получим.

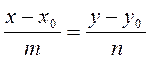
4.1.4 Параметрические уравнения прямой.

Если в уравнении прямой, проходящей через заданную точку параллельно заданному вектору, приравнять оба равенства некоторому параметру t:

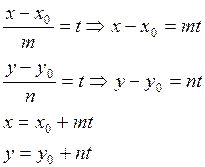
полученные уравнения называются параметрическими уравнениями прямой.

4.1.5 Уравнение прямой проходящей через 2 заданные точки.

Пусть прямая проходит через две точки М₁(х₁,у₁) и М₂(х₂,у₂)  (Рис. 4.3)

                           у

                                                        М(х,у)

                                                    М₂(х₂,у₂)

М₁(х₁,у₁)

0

                                                                                    х

Рис 4.3

Возьмём произвольную точку на прямой и рассмотрим два вектора  и

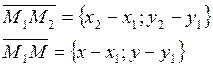
векторы  и лежат на одной прямой, то есть они колинеарны и, следовательно, из условия колинеарности двух векторов имеем:

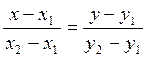
4.1.6 Уравнение прямой в отрезках.

Рассмотрим прямую, которая пересекает оси координат в точках А(а,0) и В(0,в) при этом  (Рис 4.4)

                                             у

 

                                                  В(0,в)

0

                                                                 А(а,0)

                                                   х

Рис 4.4

Воспользуемся уравнением прямой проходящей через 2 заданные точки

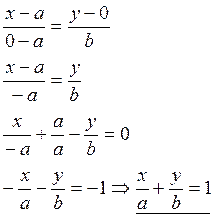
Это уравнение называется уравнением прямой в отрезках.

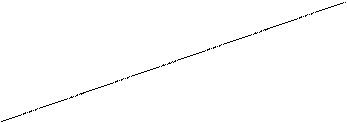
4.1.7 Уравнение прямой с угловым коэффициентом.

Угол наклона прямой к оси ОХ называется угловым коэффициентом.

   

                                                 у

 

                                                   

 

х

Рис. 4.5

Данное уравнение можно записать для любой прямой, кроме прямых перпендикулярных оси ОХ, так как в этом случае, 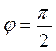а - не определён.

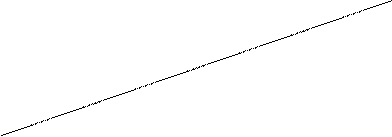
4.1.8 Уравнение прямой проходящей через заданную точку с данными угловыми коэффициентами.

Пусть прямая не перпендикулярна оси ОХ и проходит через точку М₀(х₀,у₀)

                                                  у

 

                                                   

 

х

Рис. 4.6

у-у₀=к(х-х₀) – это и будет уравнение такой прямой.

Мы рассмотрели различные способы задания уравнения прямой на плоскости. Такое многообразие уравнений существенно облегчает решение различных задач по аналитической геометрии.

4.2 Угол между прямыми.

Условие параллельности и перпендикулярности прямых. Расстояние от точки до прямой.

Пусть заданы две неперпендикулярные прямые. Углом между ними будем называть меньший из углов образованных этими прямыми.

В случае если прямые заданы уравнениям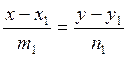и.

 и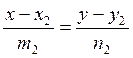

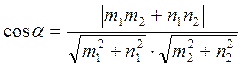
В случае если прямые заданы общими уравнениями.

А₁х+В₁у+С₁=0                А₂х+В₂у+С₂=0

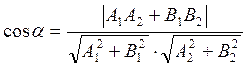
В случае если прямые заданы уравнениями с угловыми коэффициентами:

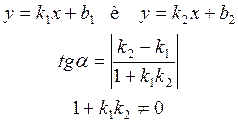
Рассмотрим теперь случай, когда прямые параллельны.

Для различных уравнений имеют различные условия параллельности:

1.

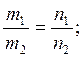
2.

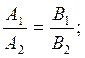
3.

Условие перпендикулярности прямых также различны для различных уравнений:

1.        

2.        

3.