Прямая на плоскости. Виды уравнения прямой на плоскости. Уравнение прямой проходящей через заданную точку перпендикулярную заданному вектору, страница 3

-4х-3у-1=0

4х+3у+1=0 – искомая прямая

Пример 5:

На прямой 2х+у-5=0 найти точку С, равноудалённую от точки А(5;5),      В(-2;4)

Решение:

Сделаем схематический чертёж (Рис. 4.11)

                              А

                                                                                         В

 

С(х_с,у_с)

Рис. 4.11

По условию задачи расстояние от точек А и В до прямой одинаковы, то есть . Обозначив координаты точки С(х_с,у_с), запишем первое условие:

         

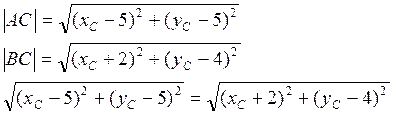
Так как точка С лежит на заданной прямой, то второе условие получается после подстановки координат точки С в уравнение заданной прямой.

2х_с+у_с-5=0

Рассматривая совместно эти два условия получим систему двух уравнений с двумя неизвестными

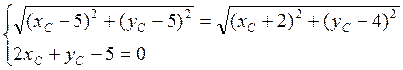
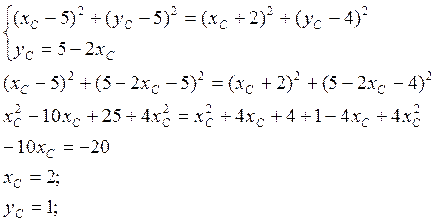
Таким образом координаты искомой точки С(2,1)

Пример 6:

Даны две стороны параллелограмма 2х-3у-1=0, 3х-4у-2=0 и точка Е(3,2) пересечение его диагоналей. Составить уравнение двух других его сторон.

Решение:

Сделаем схематический чертёж (Рис 4.12)

В                                               С

    

Е(3,2)

                            А                                                 D

Рис. 4.12

Две заданные стороны параллелограмма пересекаются в точке А, поэтому решая совместно систему уравнений найдём координаты точки А.

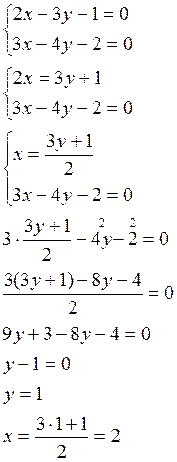
А(2,1)

Используя свойства параллелограмма, что диагонали в точке пересечения делятся пополам найдём координаты точки С

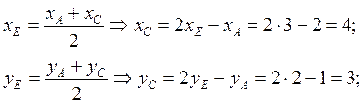
С(4,3)

Зная координаты точки С легко найти уравнения сторон параллелограмма ВС и DC.

Ищем уравнение ВС в виде . Так как стороны ВС и AD параллельны и уравнение стороны AD известно:

3х-4у-2=0, то используя условие параллельности двух прямых, получим:

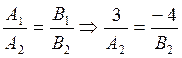
тогда можно принять А₂=3, В₂=-4 и уравнение ВС

3(х-4)+(-4)(у-3)=0

3х-12-4у+12=0

3х-4у=0

Аналогично используя параллельность сторон параллелограмма CD и АВ: 2х-3у-1=0, получим уравнение CD в виде:

2(х-4)+(-3)(у-3)=0

2х-8-3у+9=0

2х-3у+1=0

Пример 7:

Найти точку симметричную точке Р (10,21) относительно прямой

2х+5у-38=0.

Решение:

Сделаем схематический чертёж (Рис. 4.13)

 

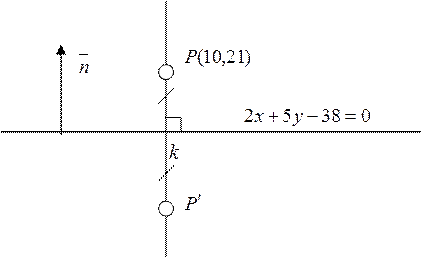Рис. 4.13

Найдём уравнение прямой, проходящей через точку Р. перпендикулярную заданной прямой. Из уравнения заданной прямой 2х+5у-38=0 легко определяются проекции вектора перпендикулярного заданной прямой , этот вектор . Тогда используем уравнение прямой, проходящей через заданную точку параллельно заданному вектору, причём в качестве такого вектора берём вектор .

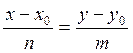
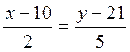
преобразуем уравнение к общему виду.

5(х-10)=2(у-21)

5х-50-2у+42=0

5х-2у-8=0

Найдём координаты точки К, как точки пересечения прямых 2х+5у-38=0 и 5х-2у-8=0, решая совместно систему двух уравнений с двумя неизвестными.

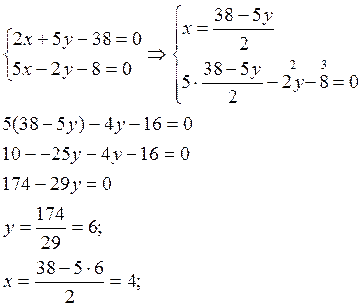
таким образом, координаты точки К(4,6)

зная координаты точки К и точки Р и используя то, что точка К является серединой отрезка РР^/ найдём координаты точки Р^/

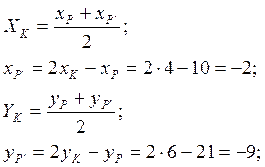
искомая точка Р^/ имеет координаты Р^/(-2,-9).

Пример 8:

Даны вершина треугольника А(-2,3) его медианы 5х-2у-10=0 и 7х+5у-27=0. составить уравнение сторон треугольника.

Решение:

Прежде всего убедимся, что заданная вершина треугольника А(-2,3) не лежит ни на одной из заданных медиан. Для этого будем подставлять координаты точек А в уравнение медиан и, если они не обращаются в тождества, это означает, что точка не лежит на прямой.

Рассмотрим медианы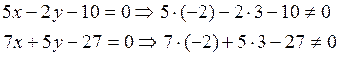   

Таким образом точка А не лежит на заданных медианах, то есть в треугольнике АВС нам заданны уравнения медиан ВК и СМ. сделаем схематический чертёж. (Рис. 4.14)