Прямая на плоскости. Виды уравнения прямой на плоскости. Уравнение прямой проходящей через заданную точку перпендикулярную заданному вектору, страница 4

 

Рис. 4.14

Найдём координаты точки  В(х_в,у_в)

Так как точка В лежит на медиане ВК, то она обращает уравнение ВК в тождество

5х_в-2у_в-10=0

Выразим координаты точки М, как серидины отрезка АВ через координаты точек А и В.

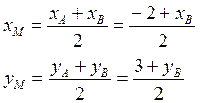
Подставляя координаты точки М в уравнение медианы СМ, получим второе уравнение:

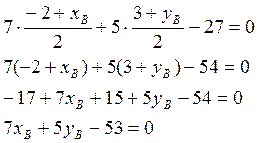
получим систему двух уравнений с двумя неизвестными.

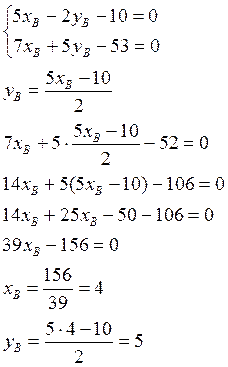
Таким образом, точка В имеет координаты В(4;5)

Зная координаты точек А и В запишем уравнение сторон треугольника АВ, как прямой проходящей через 2 заданные точки.

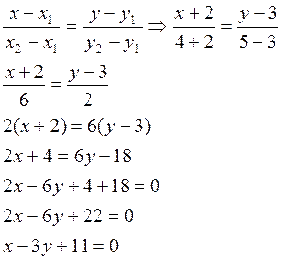
Координаты точки С, находим аналогично. Точка С(х_с,у_с) лежит на медиане СМ

7х_с+5у_с-27=0

Точка К лежит на медиане ВК

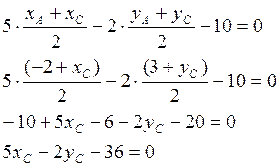
Получим систему уравнений

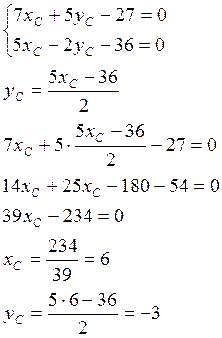
Таким образом точка С имеет координаты С(6;-3).

Зная координаты точек А и С находим уравнение сторон АС

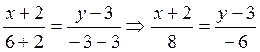
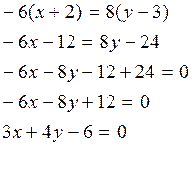
Зная координаты точек В и С найдём уравнение сторон ВС

 

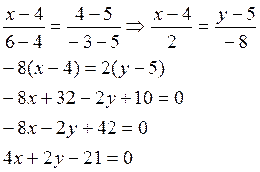
Таким образом мы нашли уравнение всех трёх сторон треугольника:

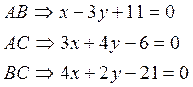
Пример 9:

Даны две вершины треугольника А(-2;2), В(10;8) и точка пересечения  его высот Н(1;6). Найти координаты третьей вершины треугольника.

Решение:

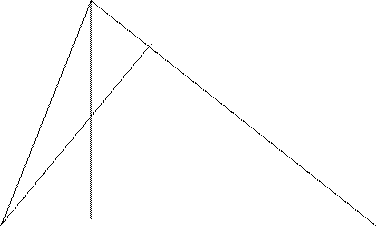
Сделаем схематический чертёж к задаче (Рис 4.15)

А   

 

Н

                       

                   В                                                                    С

Рис. 4.15

Используя уравнение прямой, проходящей через заданную точку перпендикулярно заданному вектору, найдём уравнение сторон АС и ВС. Для нахождения уравнения АС найдём вектор , который перпендикулярен стороне АС.

тогда уравнение  АС

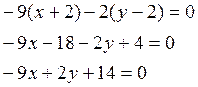
Для нахождения уравнения ВС, найдём вектор , перпендикулярной стороне ВС.

тогда уравнение ВС

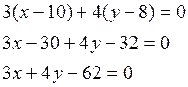
Стороны АС и ВС пересекаются в точке С, поэтому для нахождения её координат рассмотрим систему уравнений, в которую входят уравнения прямой АС и прямой ВС.

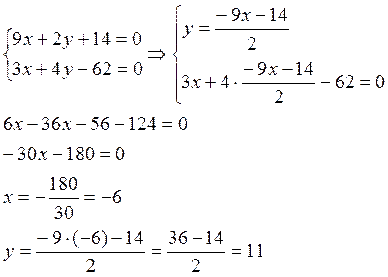
Таким образом координаты точки С(-6;11)

Задачи для самостоятельного решения

1.  Составить уравнение прямой проходящей через точку А(2;-3) перпендикулярную прямой, заданной уравнением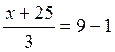

2.  Найти расстояние от точки А(1;2) до прямой 4х+3у-5=0

3.  Найти координаты точки В симметричной точке А(1;3) относительно прямой 2х+у-10=0

4.  Через точку пересечения прямых х-2у-5=0 и 2х-3у-8=0 провести прямую параллельную прямой 3х-2у+2=0

5.  Стороны треугольника выражаются уравнениями х+3у-2=0; 2х+у+5=0; 3х-4=0. найти уравнения высот треугольника.

6.  Вершины треугольника А(2;1), В(0;7), С(-4;-1). Найти уравнения медиан треугольника и координаты точки их пересечения.

7.  Найти уравнение прямой, проходящей через начало координат и через точку пересечения медиан треугольника, стороны которого выражаются уравнениями х-у-4=0, 2х-11у+37=0, 2х+7у-17=0

8.  Найти координаты точки равноудалённой от трёх точек А(2;3), В(4;2), С(-1;0).

9.  Даны две вершины равностороннего треугольника АВС; А(2;1), и В(2;5). Найти координаты третьей вершины С.

10. На прямой х+3у=0 найти точку, равноудалённую от начала координат  и от прямой х+3у-2=0.

11. Найти расстояние между параллельными прямыми 3х+4у-15=0, 3х+4у+20=0.

12. Найти уравнения биссектрис углов образуемых прямыми 3х+4у-9=0 и 12х+9у-8=0. Проверить, что эти биссектрисы перпендикулярны друг другу.

13. Даны центр квадрата С(-1;0) и уравнение стороны х+3у-5=0. найти уравнения трёх его других сторон.

14. Найти уравнение биссектрисы внешнего угла А треугольника с вершинами А(0;0), В(3;0), С(0;7).

15. В прямоугольном равнобедренном треугольнике даны уравнение катета у=2х и середина гипотенузы К(2;4). Найти  уравнения двух других сторон треугольника.