Прямая на плоскости. Виды уравнения прямой на плоскости. Уравнение прямой проходящей через заданную точку перпендикулярную заданному вектору, страница 2

Если задана прямая общим уравнением Ах+Ву+С=0 и некоторая точка М(х₁,у₁) не лежащая на прямой, то расстояние от этой точки до заданной прямой определяется формулой:

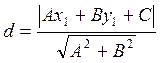
Рассмотрим примеры решения задач по теме главы 4.

Пример 1:

Даны вершины треугольника А(3,2); В(-1,5); С(1,-2). Составить уравнение высоты ВD и найти её длину.

Решение:

Сделаем схематический чертёж (Рис 4.7)

В

 

                          

А             D                          С

Рис. 4.7

Найдём  проекции вектора

Имеем вектор , перпендикулярный исковой прямой и точку В, через которую проходит прямая. Воспользуемся уравнением прямой, проходящей через заданную точку и перпендикулярную заданному вектору.

          А(х-х₀)+В(у-у₀)=0

В нашем случае А= -2;  В= -4; х₀= -1; у₀= 5. Тогда имеем

–2(х-(х-1)+(-4)(у-5)=0

При решении задач по аналитической геометрии все полученные уравнения будем преобразовывать к общему уравнению прямой. Тогда  в нашем случае получим:

-2х-2-4у+20=0

-2х-4у+18=0

или

2х+4у-18=0

полученное уравнение можно поделить на 2

х+2у-9=0 – это и есть искомое уравнение в виде общего уравнения прямой на плоскости.

Для нахождения длины высоты BD воспользуемся формулой расстояния от точки до заданной прямой. Но для этого необходимо найти уравнение прямой АС. Найдём уравнение прямой АС, как уравнение прямой, проходящей через 2 заданные точки А и С.

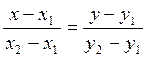
Пусть А – первая точка,

С – вторая точка

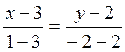
преобразуем полученное уравнение к общему виду.

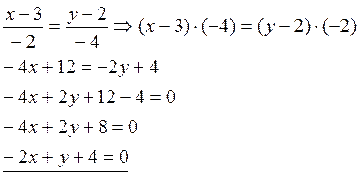
Полученное уравнение и будет уравнением АС в общем виде. Тогда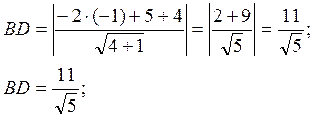

Пример 2:

Даны вершины треугольника А(3,2);В(-1,5);С(1,-2). Составить уравнение медианы ВК и найти её длину.

Решение:

Сделаем схематический чертёж (Рис 4.8)

В

 

А

К                 

С

Рис 4.8

Найдём координаты точки К, как середины отрезка АС.

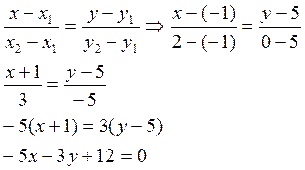
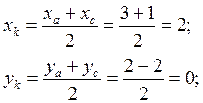
Найдём уравнение ВК, как прямой, проходящей через 2 точки.

Полученное уравнение – уравнение медианы.

Длину медианы ВК найдём как расстояние между двумя точками на плоскости, заданными своими координатами.

длина медианы ВК

Пример 3:

Даны вершины треугольника А(3,2); В(-1,5); С(-5,-3).Составить уравнение биссектрисы ВN и найти её длину.

Решение:

Сделаем схематический чертёж (Рис. 4.9)

В       

 

А                  N               С

Рис. 4.9

Для нахождения координат точки N воспользуемся теоремой о биссектрисе, известно из средней школы, что биссектриса делит противоположную сторону треугольника в том отношении, как относятся соответствующие прилегающие стороны таким образом:

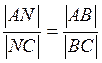
найдём длины сторон треугольника  и

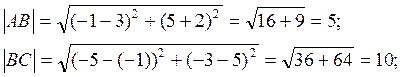
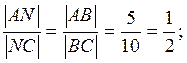
обозначим отношение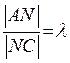

Далее используем формулу деления отрезка в заданном отношении.

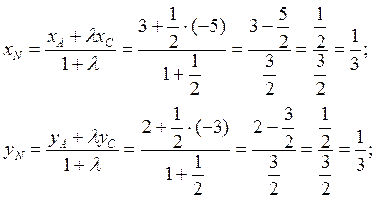
таким образом, координаты точки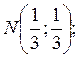

Используя уравнение прямой проходящей через 2 заданные точки, получим:

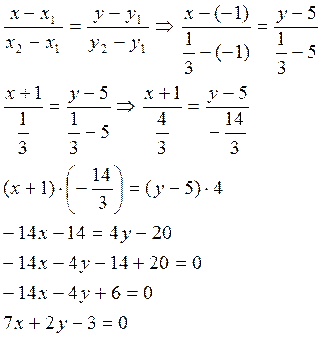
уравнение биссектрисы ВN.

Для нахождения длины биссектрисы BN воспользуемся формулой:

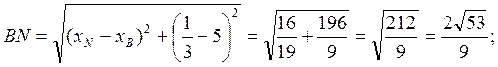
Пример4

Составить уравнение прямой, проходящей через точку А(2;-3) перпендикулярную прямой, заданной уравнением 3х-4у+2=0

Решение

Сделаем схематический чертёж (Рис 4.10)

 

                                                   А(2;-3)

 

Рис. 4.10

Из уравнения заданной прямой определяем проекции вектора  перпендикулярного заданной прямой . По условию задачи этот вектор параллелен искомой прямой. Тогда воспользуемся уравнением прямой проходящей через заданную точку параллельно заданному вектору.

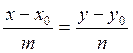
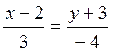
Преобразуем полученное уравнение к общему виду.

(х-2)(-4)=(у+3)3

-4х+8=3у+9

-4х-3у+8-9=0