Глава 7 Системы линейных уравнений.
7.1 Основные понятия.
Определение 1:Системой линейных уравнений называется система вида:
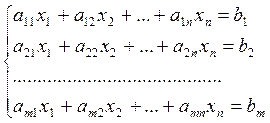
Определение 2: Решением системы линейных уравнений называется
упорядоченный набор чисел ![]() при
подстановке которых в исходную систему каждое из уравнений обращается в
тождество.
при
подстановке которых в исходную систему каждое из уравнений обращается в
тождество.
Определение 3: Основной матрицей системы линейных уравнений
называется матрица А размерности ![]() ,
образованная из коэффициентов при неизвестных:
,
образованная из коэффициентов при неизвестных:
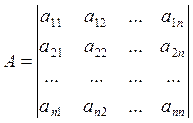
Определение 4: Основная матрица А системы дополненная
столбцом свободных членов, называется расширенной матрицей системы и
обозначается ![]() .
.
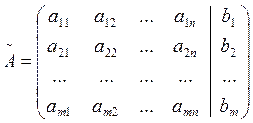
Определение 5: Система уравнений называется совместной, если она имеет хотя бы одно решение и несовместной если у неё нет.
Определение 6: Система уравнений называется однородной, если все свободные члены равны нулю.
Определение 7: Неизвестная хi в системе линейных уравнений называется базисной, если она встречается в единственном уравнении системы и имеет коэффициент равный единице.
Определение 8: Система уравнений имеет базисный вид, то есть приведена к единичному базису, если в каждом уравнении выделена одна базисная переменная.
Приведём системы базисного вида:
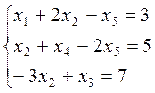
Расширенная матрица этой системы:
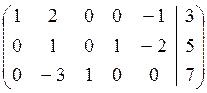
Нетрудно увидеть, что базисными переменными в приведённом примере являются переменные х1, х3, х4.
Определение 9: Переменные входящие в уравнения системы и не являющиеся базисными называются свободными переменными.
Определение 10: Две системы линейных уравнений называются равносильными, если множества их решений совпадают. Все несовместные системы равносильны.
Перечислим элементарные преобразования систем, приводящие к равносильным системам:
1. Удаление из системы нулевого уравнения 0х1+0х2+…+0х4=0
2.
Умножение на число ![]() правой и левой части любого
уравнения.
правой и левой части любого
уравнения.
3.
Прибавление к левой и
правой части i-ого уравнения соответствующих частей j –
ого уравнения, умноженных на число ![]() .
.
4. Перестановка местами i-ого и j-ого уравнений.
7.2 Решение системы линейных уравнений методом Жордана-Гаусса.
Этот метод позволяет привести к базисному виду совместную систему уравнений.
Элементарные преобразования будем осуществлять по следующей схеме.
1. Выбираем разрешающий элемент в каком либо уравнении и если этот элемент расширенной матрицы не является единицей, то элементы разрешающей строки делим на этот элемент.
2. Разрешающий столбец с помощью элементарных преобразований заполняем нулями.
3. Получаем новую расширенную матрицу, в которой снова выбираем другую разрешающую строку и повторяем все действия.
4. В случае возникновения нулевой строки ее вычеркиваем.
5. В случае возникновения строки вида: 0х1+0х2+0хn=bi система не имеет решений, то есть является несовместной.
Рассмотрим пример решения системы с использованием столбца контрольных сумм КΣ, которые представляют собой суммы всех коэффициентов, соответствующих уравнений. Эти числа преобразуются по тем же правилам, что и остальные элементы матрицы. Контроль состоит в том, что на каждом этапе проверяется совпадение контрольной суммы с суммой всех коэффициентов данного уравнения. Решим систему уравнений.
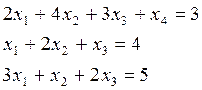
Составим расширенную матрицу системы, причем в первом столбце будут контрольные суммы, а в последнем будем указывать базисные переменные. Легко видеть что в первом уравнении такой переменной будет переменная х4.
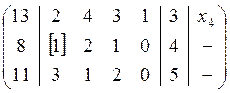
выберем разрешающий элемент во второй строке, пусть
это будет ![]() . Используя элементарные
преобразования, получим матрицу у которой все остальные элементы разрешающего
столбца были нулевые, для этого выполняются следующие элементарные
преобразования:
. Используя элементарные
преобразования, получим матрицу у которой все остальные элементы разрешающего
столбца были нулевые, для этого выполняются следующие элементарные
преобразования:
1. Разрешающая строка умножается на (-2) и складывается с первой строкой, результат записываем на место первой строки.
2. Разрешающая строка умножается на (-3) и складывается с третьей строкой, результат записывается на место третьей строки.
В результате получаем матрицу:
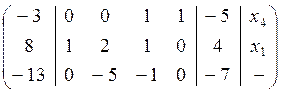
Используя столбец контрольных сумм, сделаем проверку:
-3=0+0+1+1-5
8=1+2+1+0+4
-13=0-5-1+0-7
Следующим шагом необходимо выбрать разрешающий элемент
в третьей строке. В качестве такого элемента можно взять элемент ![]() , но для того чтобы этот элемент
стал равным единице, умножим элементы третьей строки на (-1). Получим матрицу
вида:
, но для того чтобы этот элемент
стал равным единице, умножим элементы третьей строки на (-1). Получим матрицу
вида:
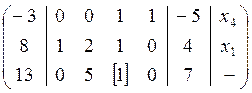
используя элементарные преобразования, преобразуем разрешающий столбец матрицы так, чтобы все элементы кроме разрешающего (базисного) стали равны нулю, для этого выполняем следующие элементарные преобразования.
1. Разрешающая строка умножается на (-1) и складывается со второй строкой, результат записывается на место второй строки.
2. Разрешающая строка умножается на (-1) и суммируется с первой строкой, результат записывается на место первой строки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.