Арифметическое n-мерное векторное пространство. Арифметические векторы и их обозначение. Линейно зависимые и линейно независимые системы векторов

Глава 8 Арифметическое n-мерное векторное пространство.

8.1 Арифметические векторы.

Выше мы дали понятие вектора на плоскости и в пространстве.

На плоскости вектор определяется двумя координатами, то есть парой чисел. В пространстве вектор определяется уже тройкой чисел. Причём в этих случаях возможна была геометрическая интерпретация. Во многих задачах экономики приходится встречаться с величинами, которые определяются гораздо большим числом характеристик чем три. Поэтому обобщим понятие вектора на тот случай, когда число характеристик равно n.

Определение 1:     Арифметическим n - мерным вектором называется любая последовательность из n действительных чисел:

а₁, а₂,…,а_n

Обозначать арифметический вектор будем как и обычный вектор чертой сверху, числа а₁, а₂, …, а_n называются компонентами или координатами вектора.

Пример:

Имеем арифметический вектор с координатами –1, 2, 3, 0, 1.

Многие определения, введённые для векторов, на плоскости и в пространстве фактически обозначаются на случай двух координат. Тем не менее, повторим их.

Определение 2:     Дав вектора и с одинаковым числом координат:

называются равными если: а₁=b₁; а₂=b₂…a_n=b_n.

равенство векторов записывают: .

Определение 3:     Вектор, у которого все компоненты равны нулю, называется нулевым вектором (0,0,…0).

Обозначается:  .

Определение 4:     Суммой двух векторов  и  называется вектор

Определение 5:     Произведением вектора  на число  называется вектор.

Операции сложения двух арифметических векторов и умножение арифметического вектора на число обладает следующими свойствами.

1.   - коммутативность сложения.

2.   - ассоциативность сложения.

3.   - для любого .

4.  Для любого вектора  существует такой вектор , что +=0.

5.   - дистрибутивность относительно суммы векторов.

6.   - дистрибутивность относительно суммы чисел.

7.   - ассоциативность относительно умножения на число.

8.   - существование нейтрального элемента при умножении.

Приведённые свойства почти очевидны и являются следствиями свойств сложения и умножения чисел.

Определение 6:     Арифметическим n – мерным пространством называется множество всех n – мерных арифметических векторов с введёнными выше операциями сложения векторов и умножения вектора на число. Обозначается Rⁿ.

Очень важным понятием для арифметических векторов является скалярное произведение, но для арифметических векторов оно определяется несколько иначе.

Определение 7:     Скалярным произведением двух векторов  и  называется число .

Скалярное произведение обладает теми же свойствами, которые были введены для трёхмерных векторов.

Модуль арифметического n – мерного вектора определяется, так же как и в трёхмерном пространстве.

Аналогично вводится и понятие угла между двумя не нулевыми векторами.

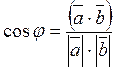
Определение 8:     Неравенство Коши-Буияковского. Для любых двух векторов  и  из пространства Rⁿ справедливо неравенство:         

Определение 9:     Два арифметических вектора  и

 называются ортогональными если их скалярное произведение равно нулю.  или .

8.2 Линейно зависимые и линейно независимые системы векторов.

Прежде чем ввести понятие линейной зависимости векторов, дадим определение системы векторов.

Определение 1:     Если мы имеем дело не с одним, а несколькими векторами, то есть набор векторов  - называется системой векторов.

Определение 2:     Пусть даны векторы  из арифметического пространства Rⁿ. Любой вектор  вида:

, где  какие угодно числа называется линейной комбинацией векторов .

Определение 3:     Система векторов  из арифметического пространства Rⁿ называется линейно зависимой, если существуют такие числа  не равные одновременно нулю, что справедливо равенство

Определение 4:     Система векторов  называется линейно независимой если равенство:

выполняется только в том случае, если все коэффициенты одновременно равны нулю .

Свойства линейной зависимости.

1.  Система из одного вектора линейно зависима тогда и только тогда, когда это нулевой вектор.

2.  Система, содержащая более одного вектора, линейно зависима тогда и только тогда, когда среди данных векторов имеется такой, который выражается линейно через остальные.

3.  Если часть системы векторов линейно зависима, то и вся система векторов линейно зависима. Таким образом, система, содержащая нулевой вектор, линейно зависима.

4.  Если система векторов  линейно независима, но при добавлении к ней ещё одного вектора  становится линейно зависимой, то вектор  линейно выражается через векторы

Рассмотрим систему векторов.

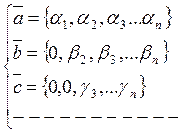
числа стоящие на диагонали отличны от нуля. Такая система векторов называется лестничной, причём число векторов в лестничной системе не превосходит n.

Любая лестничная система векторов линейно независимая.

Определение 5:     Векторы  и  из арифметического пространства Rⁿ называются коллинеарными  если  или , в координатной форме:

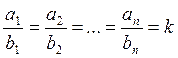
Теорема: