Кривые второго порядка. Преобразование декартовых координат на плоскости. Основные виды кривых второго порядка

Глава 9 Кривые второго порядка. Преобразование декартовых координат на плоскости.

9.1 Основные виды кривых второго порядка.

Определение 1:     Окружностью называется геометрическое место точек равноудалённых от одной точки, называемой центром окружности.

Уравнение окружности имеет вид:

x²+y²=r² - центр окружности находящийся в начале координат; r - радиус окружности.

(x-x₀)²+(y-y₀)²=r²- центр окружности в точке с координатами (x₀;y₀); r - радиус окружности.

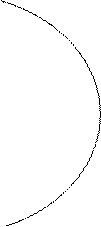
Определение №2  Эллипсом называется геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами есть величина постоянная, причём эта постоянная должна быть больше расстояния между фокусами (рис. 9.1).

Запишем уравнение эллипса с центром в начале координат.

                     

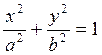
b²=а²-с²

  Числа (а) и (b) называются полуосями эллипса.

Рис 9.1

F₁;F₂- фокусы эллипса.

Отношение расстояния между фокусами 2с к длине большой полуоси эллипса 2а называется эксцентриситетом эллипса.

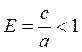
Прямые  перпендикулярные фокальной от эллипса и отстоящие от центра эллипса на расстоянии:     а/Е   называются директрисами: их уравнения имеет вид

   

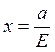
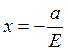
Определение 3: Гиперболой называется геометрическое место точек разность расстояний которых от двух данных точек, называемых фокусами есть величина постоянная, причём эта постоянная должна быть положительной и меньше расстояния между фокусами (рис. 9.2).

                                                           y

	B		C

                                                                   +b

                                                                                                      M         

                F₂(-c;0)              -a                                     +a         F₁(c;0)

D

A

                                                                   -b

Рис. 9.2

Уравнение гиперболы с центром в начале координат имеет вид:

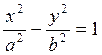
Фокальная ось - ОХ

 

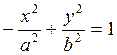
Фокальная ось - ОY

b²=c²-a²

Гипербола имеет две асимптоты уравнения которых:

                                         

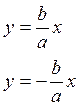
Асимптоты являются диагоналями основного прямоугольника гиперболы ABCD со сторонами 2a и 2b.

Отношение фокусного расстояния 2с к длине действительной оси гиперболы 2а называется – эксцентриситетом гиперболы и обозначается Е.

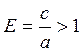
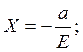
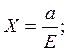Прямые перпендикулярные фокальной оси гиперболы и проходящие через точки и  называются дирректрисами гиперболы, их уравнение:

Определение 4:     Парабола есть геометрическое место точек равноотстоящих от данной точки, называемой фокусом, причём точка фокуса не лежит на дирректрисе (рис. 9.3).

 

                                                         y

 

                                                                                                                                                                                  -p/2                    F(p/2;0)                                  x

Рис. 9.3.

Уравнения параболы с вершиной  в начале координат имеют вид:

y²=2px – фокальная ось ОХ

х²=2ру – фокальная ось ОУ

Эксцентриситет параболы равен единице. Уравнение дирректрисы имеет вид:

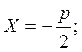
В случае если центр эллипса или центр гиперболы или вершина параболы находятся не в начале координат, а в произвольной точке с координатами (х₀,у₀) то каноническое уравнение этих линий преобразуется к виду:

Эллипс:        

Гипербола:

Парабола:

 

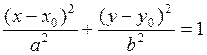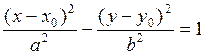Полуоси эллипса и гиперболы уже откладываются в новой системе координат, которая получается параллельным переносом начала координат в точку (х₀,у₀).

10.2 Преобразования систем координат на плоскости.

Приведение общего уравнения кривой к каноническому виду.

Будем использовать два преобразования системы координат – параллельный перенос начала координат и поворот системы координат.

Рассмотрим параллельный перенос начала координат. Если заданы две системы координат X, 0, Y  _и  X₁, 0₁, Y₁ (рис. 9.4)

                                  y             y₁                    

                                                              M

                                                 0₁                   

                       y₀             x_o                                        x₁

 

                                                                                            x       

Рис. 9.4.

Формулы, связывающие координаты точки М в старой и новой системе координат будут:

х₁=х-х₀               х=х₁+х₀

или

у₁=у-у₀               у=у₁+у₀

где  х₀, у₀ – координаты нового начала системы координат.

Теперь рассмотрим преобразование поворота системы координат X, 0, Y и X₁, 0, Y₁, при чём система X₁ 0 Y₁ повёрнута относительно исходной системы координат на угол a  (рис. 9.5).

                                     y₁             y

M

 

                                                                                                  x₁

                                                                                           

a

₀

                                                                                                 x            

Рис. 9.5.

a- угол поворота системы координат.

  Выпишем формулы связывающие координаты точки М в системе координат X, 0, Yс координатами точки М в системе координат X₁, 0, Y₁

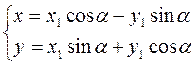Рассмотрим теперь общее уравнение кривой второго порядка.

Ах²+2Вху+Су²+2Dx+2Ey+F=0

Осуществляя поворот системы координат на угол a. Причём угол a выбирается таким образом, чтобы коэффициент при слагаемом, содержащим произведение ху стал равен нулю.

Обозначим новую систему координат X₁ 0 Y₁. В новой системе координат общее уравнение кривой будет:

А₁х₁²+С₁у₁²+2D₁x+2E₁y+F=0

Нетрудно заметить, что коэффициент F не изменился.

Если в полученном уравнении коэффициенты А₁ и С₁ одного знака т.е. если А₁С₁>0, то мы получаем кривую эллиптического типа.

Если коэффициенты А₁ и С₁ разных знаков то есть А₁С₁<0,то уравнение определяет кривую гиперболического типа.        

Если один из коэффициентов А₁ или С₁ равен нулю, то А₁С₁=0, то получаем кривую параболического вида.

Далее используя формулу параллельного переноса переходим из системы координат X₁, 0, Y₁ в систему координат X₂, 0₂, Y₂ в которой получаем канонические уравнения эллипса, гиперболы или параболы.

Пример 1:   

Найти эксцентриситет и дирректрисы эллипса заданного уравнением:

х²+2у²=2

Решение:

Приведём уравнение эллипса к каноническому виду:

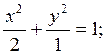Из этого уравнения видно, что

а²=2; b²=1; тогда с²=а²-b²=2-1=1

  Найдём эксцентриситет

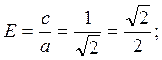Уравнения дирректрис

 

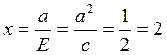
или   х=-2;

таким образом уравнения дирректрис

х=2    и        х=-2.

Пример 2:

Эллипс касается оси ординат в начале координат, а центр его находится в точке (5;0) составить уравнение эллипса, если известно, что его эксцентриситет равен 0,6.

Решение:

Для нахождения основного уравнения эллипса используем каноническое уравнение эллипса со смещённым центром.

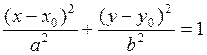        координаты центра эллипса нам заданы          х₀=5; у₀=0;

таким образом, одна из осей эллипса лежит на оси ОХ, так как эллипс касается оси ОУ в начале координат.

Рассмотрим два случая.

1случай:

Большая ось эллипса лежит на оси ОХ

Тогда   а=5;

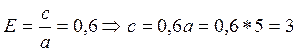
для эллипса известно что: b²=a²-c²=25-9=16

тогда искомое уравнение эллипса имеет вид:

         

         

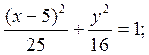
2 случай:

Малая ось эллипса совпадает с осью ОХ.

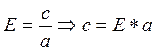Тогда   b=5;

Из                                 соотношения 

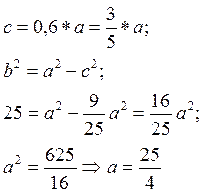
Тогда основное уравнение эллипса имеет вид:

Пример 3:

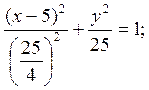
Найти уравнение эллипса расстояние между фокусами которого равно 2, а расстояние между дирректрисами равно 10.

Решение:

Воспользуемся каноническим уравнением эллипса с центром в начале