10.1 Основные типы поверхностей второго порядка.
Определение 1: Цилиндрической поверхностью называется поверхность описываемая прямой, остающейся параллельно некоторой данной прямой и пересекающей заданную линию L.
Пример цилиндрической поверхности круговой цилиндр имеет уравнение:
x2+y2=r2
Образующая параллельна оси ОZ.
В качестве второго примера рассмотрим поверхность:
у=ех
Образующая этой поверхности параллельна оси OZ, а направляющая линия расположена в плоскости ХОУ и представляет собой экспоненту у=ех.
Определение 2: Конической поверхностью называется поверхность описываемая прямой проходящей через данную точку - вершина конуса – и пересекающую данную линию – направляющую конуса. Прямая называется образующей конуса.
Простейшее уравнение кругового конуса:
х2+у2-z2=0
Вершина конуса находится в начале координат.
Рассмотрим некоторые типы поверхностей, которые носят общее название – поверхности вращения.
1. Эллипсоид вращения.
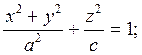
Поверхность получается вращением эллипса 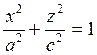 вокруг оси OZ.
вокруг оси OZ.
2. Однополосный гиперболоид вращения
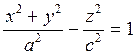 ;
;
Поверхность получается вращением гиперболы 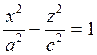 вокруг оси OZ.
вокруг оси OZ.
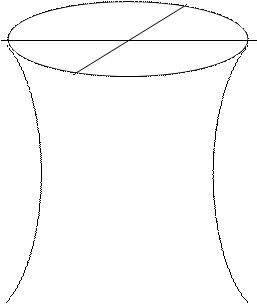
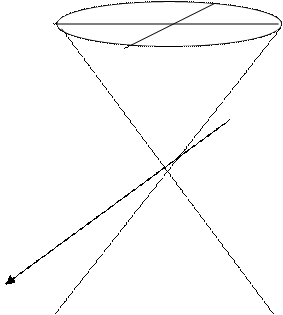
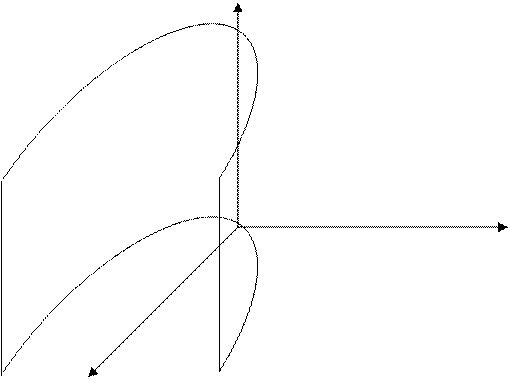
3. Двуполостный гиперболоид вращения.
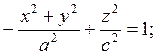
Поверхность получена вращением гиперболы 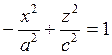 вокруг оси OZ.
вокруг оси OZ.
4. Параболоид вращения.
х2+у2=2рz
Поверхность получается вращением параболы у2=2рz вокруг оси OZ.
Рассмотренные поверхности вращения, легко обобщаются в эллиптические поверхности при замене окружности эллипсом.
Тогда имеем.
1. Эллипсоид
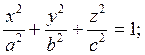 (Рис.
10.1)
(Рис.
10.1)
2. Однополосный гиперболоид
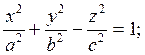 (Рис.
10.2)
(Рис.
10.2)
3. Двуполостный гиперболоид
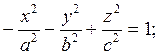 (Рис.
10.3)
(Рис.
10.3)
4. Эллиптический параболоид
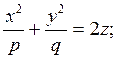 (Рис.
10.4)
(Рис.
10.4)
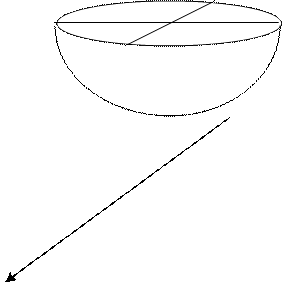
5. Конус второго порядка
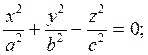 (Рис. 10.5)
(Рис. 10.5)
6. Гиперболический параболоид
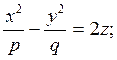 (Рис.
10.6)
(Рис.
10.6)
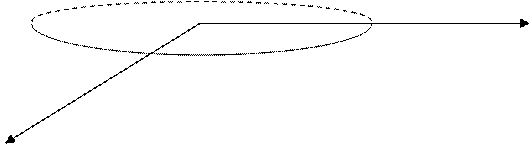
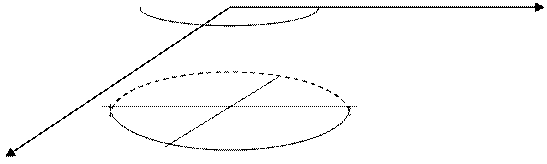
7. Цилиндры второго порядка
а) Эллиптический.
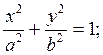 (Рис.
10.7)
(Рис.
10.7)
б) Параболический
![]() (Рис. 10.8)
(Рис. 10.8)
в) Гиперболический
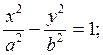 (Рис.
10.9)
(Рис.
10.9)
![]() z
z



 |
0 y
x
Рис 10.1.
z
 |
![]() y
y
 |
x
![]() z
z
 |
![]()
 0
y
0
y
![]()
x
Рис 10.3
![]() z
z
 |
![]() 0
y
0
y
X
![]() z
z
 |
0
![]() y
y
1
![]() x
x
 |
Рис 10.5
z
 |
![]()
![]()
![]() 0 y
0 y
 |
![]() x
x
Рис. 10.6
![]() z
z
 |

![]()
![]() y
y
x
 |
z
0 y
x
![]() z
z
 |
|||
0 y
x
Рис. 10.9
Рассмотрим общее уравнение поверхности второго порядка, которое преобразуется с помощью формул параллельного переноса системы координат одному из уравнений поверхности второго порядка.
Ax2+By2+Cz2+2Dx+2Ey+2Fz+G=0
Для преобразования этого уравнения будем использовать формулы параллельного переноса:
x=x0+x1
y=y0+y1
z=z0+z1
где О1(х0,у0,z0) координаты нового начала координат х1, у1, z1 новые координаты.
Рассмотрим пример преобразования общего уравнения поверхности.
Пример 1:
Определить тип поверхности и сделать её схематический чертёж.
x2+y2-z2+2x-4y+6z-6=0
Решение:
Воспользуемся формулами параллельного переноса.
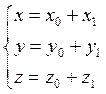
(х0+х1)2+(у0+у1)2-(z0+z1)2+2(x0+x1)-4(y0+y1)+6(z0+z1)-6=0
![]()
Преобразуем это уравнение
![]()
Найдём координаты нового начала координат, приравняв к нулю коэффициенты при х1,у1,z1, получим:
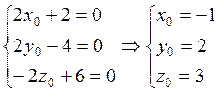
Тогда можно определить свободный член
![]()
В новой системе координат уравнение получим в виде.
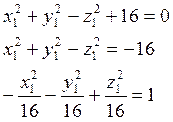
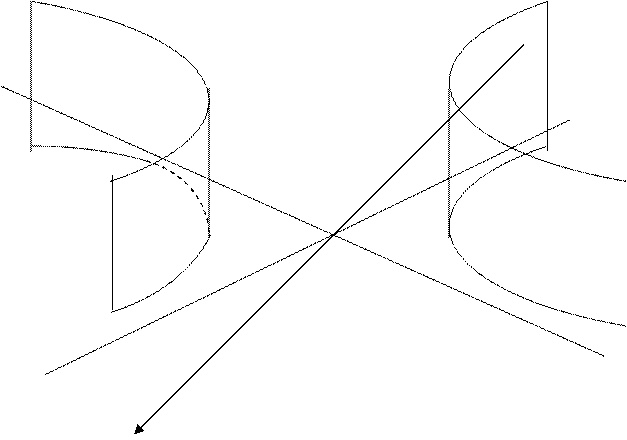
Полученное уравнение представляет собой двуполостный гиперболоид вращения относительно оси О1Z1. Изобразим его схематически. (Рис. 10.10)
![]()


![]() z
z1
z
z1
 |

![]()
![]() y1
y1
01
 |
x1
![]()
![]()
 y
y
![]()
![]()
![]() 0
0
x
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.