Выбор марки стали для конструкции. Исследование свойств монокристалла железа. Работа стали при сложном напряженном состоянии, страница 9

Критические напряжения потери устойчивости внецентренно сжатых стержней могут быть графически изображены аналогично критическим  напряжениям  при центральном сжатии, в зависимости от гибкости стержня , но кривых будет много, каждая из которых соответствует определенному относительному эксцентриситету m (рис. 7.3,в).

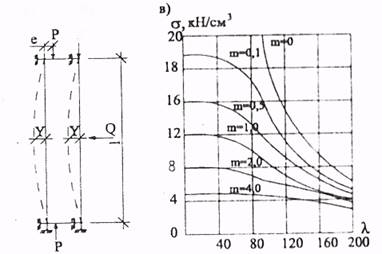
Рис. 7.3. Устойчивость внецентренно сжатых и сжато-изогнутых стержней:

а- расчетная схема внецентренно сжатого стержня; б – расчетная схема

сжато-изогнутого стержня; в – кривые критических напряжений

Так как относительный эксцентриситет характеризует влияние изгибающего момента, то можно сказать, что при заданной гибкости каждому значению изгибающего момента соответствует свое значение критического напряжения.

Для удобства расчетов, также как и при центральном сжатии,  критические напряжения при внецентренном сжатии выражают через расчетное сопротивление и коэффициент продольного изгиба при внецентренном сжатии.

                                                                           .                                                                              (7.10)

Условие устойчивости внецентренно сжатого стержня запишется

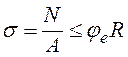                                                                           .                                                                        (7.11)

Значения коэфициента  определяется в зависимости от условной гибкости  и приведенного эксцентриситета _, определяемого по формуле , где  - коэффициент влияния формы сечения, учитывает степень ослабления сечения пластическими деформациями. Так, например, при сжатии двутаврового стержня с изгибом в плоскости стенки текучесть быстро распространяется по толщине полки, и сечение превращается в тавровое (рис. 7.4). Резкое ослабление сечения учитывается коэффициентом >1.

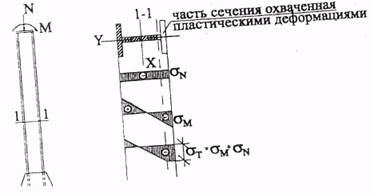
Рис. 7.4. Ослабление сечения внецентренно сжатой колонны

пластическими деформациями

В сквозных внецентренно сжатых стержнях напряжение по сечению ветвей распределяется почти равномерно, т.е. ветви работают на центральное сжатие. Поэтому расчет их на устойчивость ведут по появлению текучести в краевых волокнах и коэффициент влияния формы сечения в этих случаях не учитывают.

Необходимо также отметить, что переход части сечения в пластическую стадию работы смещает центр изгиба по отношению к сжимающей силе, в результате чего стержень не только изгибается, но и закручивается, и теряет устойчивость по изгибно-крутильной форме.

При расчете внецентренно сжатого стержня с различной жесткостью по отношению к главным осям сечения () проверки устойчивости в направлении действия момента может оказаться недостаточно. Если жесткость стержня в плоскости перпендикулярной действующему моменту меньше, есть опасность потери устойчивости стержня в этой плоскости. Так, например, для двутавра на рис. 7.4 >, следовательно, необходима проверка устойчивости стержня относительно оси y-y.

По отношению к оси y-y сила не имеет эксцентриситета и изгибающего момента не возникает, поэтому стержень должен был бы потерять устойчивость как центрально-сжатый. Однако из-за развития пластических деформаций по сечению от действия момента рабочая упругая часть сечения уменьшается, и стержень может потерять устойчивость досрочно. Поэтому для проверки устойчивости стержней в плоскости перпендикулярной действию момента (из плоскости действия момента) используется формула

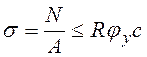                                                                           ,                                                                   (7.12)

где  - коэффициент продольного изгиба при центральном сжатии, c - коэффициент, зависящий от формы сечения, гибкости и относительного эксцентриситета и учитывающий изгибно-крутильную форму потери устойчивости стержня. Значения коэффициента c вычисляются по формулам, приведенным в нормах проектирования, они всегда меньше единицы.

Вопрос 8. Предельное состояние и расчет изгибаемых элементов.