Выбор марки стали для конструкции. Исследование свойств монокристалла железа. Работа стали при сложном напряженном состоянии, страница 8

Таким образом, устойчивость центрально-сжатого стержня будет обеспечена, если напряжения в нем будут меньше критических

                                                                           .                                                                                     (7.4)

Для удобства расчетов критическое напряжение выражают через расчетное сопротивление стали - R и коэффициент продольного изгиба - :

                                                                           .                                                                                (7.5)

Коэффициент  понижает расчетное сопротивление стали до значений критических напряжений и определяется как отношение критических напряжений стержня с учетом случайных эксцентриситетов -  к пределу текучести стали -: .

Очевидно, что коэффициент  может интересовать нас только при значениях <1, так как в противном случае будет >, т.е. более опасной является потеря несущей способности из-за потери прочности, так как условие  наступит раньше, чем .

Формула для проверки устойчивости стержня сжатого осевой силой запишется

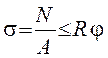                                                                           ,                                                                             (7.6)

где N = Р - продольное осевое усилие в стержне.

Значение коэффициента  можно определить по формулам или по таблицам, приведенным в нормах проектирования. Величина его зависит от расчетного сопротивления стали и гибкости стержня

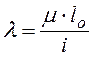                                                                           ,                                                                                 (7.7)

где  - геометрическая длина стержня;  - коэффициент приведения к расчетной длине, величина которого зависит от условий закрепления стержня по концам.

Величина критических напряжений, а следовательно, и значения коэффициентов  зависит от вида диаграммы работы материала , которая для разных марок сталей различна (рис. 7.2,а). Однако при построении диаграмм растяжения стали в относительных безразмерных параметрах  и , где расчетное сопротивление , их вид на участке <<1 (до перехода стали в пластическое состояние) приблизительно совпадает (рис. 7.2,б). Это дает возможность принять для всех марок стали унифицированную диаграмму работы (рис. 7.2,в).

Значения всех параметров в расчетах на устойчивость получены в нормах проектирования на основе такой унифицированной диаграммы.

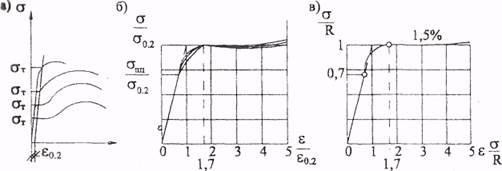
Рис. 7.2. Унификация диаграмм работы сталей:

а – диаграммы работы сталей различной прочности; б – то же, в относительных

 координатах; в – унифицированная диаграмма работы сталей

Устойчивость внецентренно сжатых стержней.

Если на стержень действует только продольная сила - Р, но приложенная с эксцентриситетом - е, стержень будет внецентренно сжат. Если к стержню приложена осевая сила Р, вызывающая продольное усилие N, и поперечная нагрузка Q, вызывающая изгибающий момент М, стержень будет сжато изогнут. Работа стержней в этих случаях мало отличается, поэтому сжато-изгибаемые элементы при рассмотрении критического состояния потери устойчивости приравниваются к внецентренно сжатым, имеющим эксцентриситет  (рис. 7.3,а,б).

При определенных значениях продольной силы и изгибающего момента внецентренно сжатые стержни также теряют устойчивость, причем критическая сила Р_сr будет естественно меньше, чем при центральном сжатии, так как потере устойчивости способствует изгибающий момент. Наибольшие краевые напряжения при действии продольной силы и момента определяются по формуле

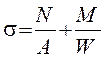                                                            .                                                                              (7.8)

Учитывая известные зависимости (эксцентриситет приложения силы , радиус ядра сечения , относительный эксцентриситет ), преобразуем выражение (7.8):

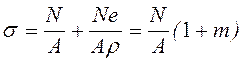                                                            .                                                          (7.9)