Выбор марки стали для конструкции. Исследование свойств монокристалла железа. Работа стали при сложном напряженном состоянии, страница 7

Ecли прямой стержень сжимать центрально приложенной силой Р, то вначале стержень будет оставаться прямым, а при незначительном отклонении, под  влиянием какого-либо воздействия, он возвращается в первоначальное состояние. Объясняется это тем, что внешняя сжимающая сила не может преодолеть сопротивление стержня тому незначительному изгибу, которому он подвергался при отклонении, а внутренняя упругая работа деформации изгиба стержня, полученная вследствие отклонения оси (потенциальная энергия изгиба (), больше внешней работы (), которую совершила сжимающая сила. Однако при увеличении сжимающей силы может наступить момент, когда ее работа будет равна работе деформации изгиба, вызванного любым, достаточно малым возмущающим фактором, т.e.  Это значение сжимающей силы называется критическим -. При достижении силой критического значения прямолинейная форма  равновесия стержня перестает быть устойчивой. Стержень может прогнуться в плоскости наименьшей жесткости, и устойчивой формой равновесия станет криволинейная форма (рис. 7.1,а).

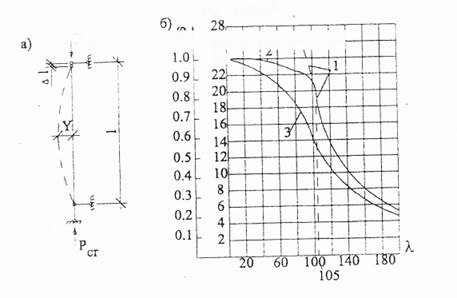
Рис. 7.1. Продольный изгиб центрально-сжатых стержней:

а – стержень с шарнирными соединениями по концам; б – кривые критических

напряжений и коэффициента продольного изгиба малоуглеродистой стали:

1 – кривая Эйлера; 2 – кривая критических напряжений с учетом пластической

работы материала; 3 – кривая коэффициента j

Если стержень имеет небольшую первоначальную кривизну (или незначительную внецентренность сжимающей силы), то при возрастании сжимающей силы он сразу же отклоняется от прямой. Это отклонение вначале мало, но когда сжимающая сила приближается к критической, отклонения становятся значительными, что означает переход в неустойчивое состояние. Дальнейшее самое незначительное увеличение сжимающей силы > приводит к резкому нарастанию деформаций и потере несущей способности стержня.

Критическая сила для упругого, ценрально-сжатого, шарнирно-опертого по концам стержня впервые была определена Л. Эйлером в  1744 году:

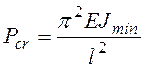                                                                           ,                                                                    (7.1)

где Е - модуль упругости металла; J_min - минимальный момент инерции стержня; l - длина стержня.

Напряжение, которое возникает в сечении стержня от критической силы, называется критическим напряжением:

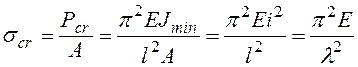                                             ,                                             (7.2)

где  - площадь поперечного сечения стержня без учета возможных ослаблений; - минимальный радиус инерции стержня;  - гибкость стержня.

Из (7.2) видно, что величина критического напряжения зависит только от гибкости стержня, так как числитель  - величина постоянная в пределах работы стали до напряжений, равных пределу пропорциональности - (рис. 4.1).

Графически зависимость критических напряжений от гибкости изображается гиперболой (рис. 7.1,б). Учитывая, что для обычной малоуглеродистой строительной стали Е = 2,06·10⁵ МПа, а 200 МПа, из (7.2) можно получить наименьшую гибкость, выше которой будет справедлива формула Эйлера

                                             .                                                  (7.3)

Критические напряжения для стержней малой (<30) и средней (30<<100) гибкости получаются больше , но меньше  (предела текучести) и теоретическое определение  критических напряжений таких стержней значительно усложняется, так как потеря устойчивости их происходит при частичном развитии пластических деформаций и переменном значении модуля упругости - Е_пл. Эти критические напряжения, определяемые сложными математическими выражениями, изображены графически кривой 2 на рис. 7.1,б.

Абсолютно прямолинейный стержень  является идеализированной расчетной схемой. Все реальные стержни в натуре имеют неизбежные отклонения от прямолинейности (случайные эксцентриситеты). Поэтому любой, так называемый центрально-сжатый стержень, с самого начала работает как внецентренно-сжатый с малым эксцентриситетом. Величина случайных эксцентриситетов определяется статистическим изучением реальных стержней. Кривая критических напряжений для центрально-сжатых стержней с учетом случайных эксцентриситетов приведена на рис. 7.1,б (кривая 3).