Applied stochastic models in business and industry. Trend estimation of financial time series, страница 7

In the present case, the selection of the smoothing constant for a nondaily series will be based on a time domain methodology that produces an equivalent constant, in the sense of producing the same percentage of smoothness as that obtained with a daily series. We start by considering the type of aggregation that links a lower-frequency series  with a higher-frequency series {Y_t}. The aggregation is assumed to be linear, that is

k

Y_T^∗ =  cjYk(T−1)+^j  for T =1,...,n      (19) j=1

with n=N/k, where x denotes the integer part of a real number x, and k is the number of observations Y_t between two successive observations Y_T∗. The c_js are constants that define the type of aggregation, e.g. c₁=···=c_k =1 are used to aggregate a flow series and c₁=···=c_k =1/k are used when working with an index or an annualized flow series (which is also considered a flow series). When working with a series of stocks, the aggregated series is generated by systematic sampling. In that case the usual values are c₁=1, c₂=···=c_k =0 or c₁=···=c_k−1=0, c_k =1.

Without loss of generality, in what follows we shall assume that c₁=···=c_k =1 for a flow series and c₁=···=c_k−1=0, c_k =1 for a series of stocks. Thus, let T and t be the time sub-index for the aggregated and disaggregated series, respectively, then we have

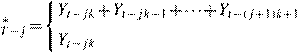for flows

Y,                                                                              j =0,1,...,T −1  (20) for stocks

The model to be applied to the aggregated data preserves the form (12)–(13), in particular the order of integration (as shown by Brewer [17]), that is,

                                                Y^∗ =s^∗+g∗            with E(g∗)=0,          Var(g∗)=∗²I_n                                              (21)

                                         K_1ns^∗ =e∗          with E                             (22)

and E 0, where ∗ is used to denote aggregated variables. As with (15), the trend estimator is given by

                                                sˆ∗ ¹∗− ²Y∗                                                                 (23)

Even though expressions (15) and (23) are of the same form, the resulting trends are different. In fact, aggregating the trend  estimated from the disaggregated series will produce different values than those of the estimated trend  obtained directly from the aggregated series. Nevertheless, we show below that it is possible to find a smoothing constant for a disaggregated series that is equivalent to the ∗_k value for the aggregated data, in the sense of producing the same percentage of smoothness.

From Equations (21)–(22) it follows that

                                                                 ∗∗_T                                                                                         (24)

where ∇∗ is the difference operator for the aggregated series, so that  is represented by an IMA(1,1), i.e. an Integrated Moving Average model of order (1,1) whose variance ∗₀ and autocovariance ∗₁ are given by

                                                             ∗² and ∗₁=−∗²                                                                                  (25)

Similarly, from Equations (12)–(13) we know that the disaggregated series follows the IMA(1,1) model _t with variance  and covariance ₁=−². To see how the two IMA=(1+,1)+···+models relate to each other, let us first consider a flow series, i.e. let^k−¹. Since S_k∇ we have     Y_T^∗−so thatj =S_kY∇_t−kjkS_kwithY_t =

S_k       1   B          B                                  

SS_{k       T} =∇           t we get

                                                     k_t        for flows                                          (26)

Now, for a stock series we know that Y −_j t _jk and_kY_t so that the previous derivation leads us to

                                                       k_t         for stocks                                           (27)

Therefore, the autocovariance generating function (AGF) of the disaggregated series, (B)= _j B_j, is given by

for flows

(28) for stocks