Applied stochastic models in business and industry. Trend estimation of financial time series, страница 5

In Figure 1 we can appreciate the percentage of smoothness achieved by different values of N and . Figure 1(a) shows that the smoothness grows quickly as the sample size grows. When

N =50, the percentage of smoothness is higher than 90% for as small as 50, and the smoothness stays basically constant when the sample size is larger than 50, in spite of the value of . Similarly, Figure 1(b) allows us to appreciate the effect of the sample size for fixed values. For >150, the percentage of smoothness is greater than 95% in the three cases shown in that figure.

Unfortunately, from (18) it is not possible to obtain an analytic expression for as a function of N and S%. Therefore, in Table I we present the values of corresponding to some percentages of smoothness, for different lengths (sample sizes) of a daily series. These values were obtained numerically, for given values of N and S%, by solving Equation (18) for . To simplify the selection of in practical applications, we searched for an approximating function of N and S% that would provide a good fit to the values in Table I. Thus, we fitted several regression models for each S% and the estimation results of the best generic fitting model are shown in Table II. We should bear in mind that the values of produced by the regression model are just approximations to the true values in Table I. We should also notice that it is not possible to get for large values of S% when the sample size is small. Further, in Table II we require that b₁+b₀N be positive in order for to be positive. It is worth stressing that the models shown in Table II are useful to interpolate and, more importantly, extrapolate the values for larger sample sizes than those shown in Table I.

Table III shows the minimum sample sizes required to produce a percentage of smoothness at most equal to S% by using Equation (18), as they appear in Table I, and compares them with those

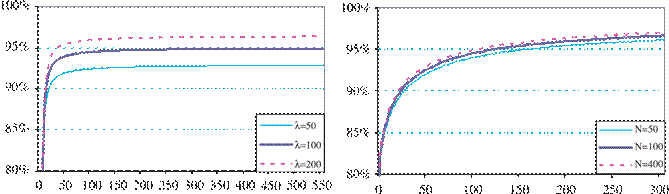
(a)                                                       N                                                     (b)                                                    λ

Figure 1. Behavior of S% for different values of and N.

Table I. Values of as a function of sample size N and S% (for a daily series).