Applied stochastic models in business and industry. Trend estimation of financial time series, страница 10

4.3. Mexican stock exchange—IPC

Data with intraday frequency of observation have become common use in finance due to the advances in data acquisition and storage. Therefore, one objective of this work is to produce a method for trend estimation of time series with intraday periodicity. In Figure 6 we plot the trend of the intraday Mexican Stock Exchange index, named IPC (which is Mexico’s most important financial index) with 55 and 65% smoothness and daily and weekly base periodicities. The sample period runs from April 17, 2006 to May 12, 2006, and covers N =19 days, so that =1.104 for S%079 for S%=65%. There are 78 observations per day, so for daily data we get k= 78= S%=55% and 162.162 for S%=65%. For this sample period there are N =3 complete 5-day weeks, thus Table II indicates =3.025 for S%=55% and =13.375 for S%=65%. Therefore, for a weekly basis we have k= 390 75 for S%=55%, and 25 for S%=65%. We did not use monthly or quarterly periodicities because the resulting sample size became smaller than N =1. It should be clear from this example that

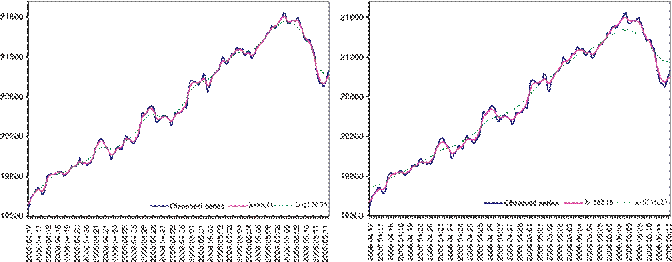
Figure 6. Intraday IPC series and trends with: S%=55%, left: daily (=86.11) and weekly (=1179.75); S%=65%, right: daily (=162.16) and weekly (=5216.25).

estimated trends for series with weekly periodicity become too smooth for low percentages of smoothness. Moreover, it is not possible to obtain trends with a weekly basis and relatively high percentages of smoothness. For the aforementioned reasons we concluded that the most suitable basis periodicity is the daily one.

5. FURTHER ILLUSTRATIVE EXAMPLES

The proposed method is now applied to some of Mexico’s financial time series to illustrate different situations that may arise in practice.

5.1. Same time series with different sample periods

In this illustration we estimate the trend of the weekly yield rate of CETES28 employed previously (see Figure 5), but with different sample periods. In fact, the sample period covers the third week of November, 2005 up to the last week of March, 2006. We have to get first the ∗ value of the weekly series equivalent to the constant used with the daily series. Since we are dealing with a stock series, the equivalent smoothing constants are related by 100 daily data the values that produce 65 and 85% smoothness of the trend are600, respectively. Therefore, for the weekly series with n=20 we get 0.369 when S%=65% and 320 when S%=85%. The resulting trends are shown in Figure 7. In particular, the trend with 85% smoothness shown in this figure resembles closely that in Figure 5. This fact can be appreciated numerically in Table IV. There we see that the trend figures are very close to each other, mainly at the middle and the end of the shorter sample period.

5.2. Time series with missing data

We now use the method to obtain the trend for the daily 5-day week IPC index. This is a stock series whose period of observation runs from November 14, 2005 to March 31, 2006. In this case

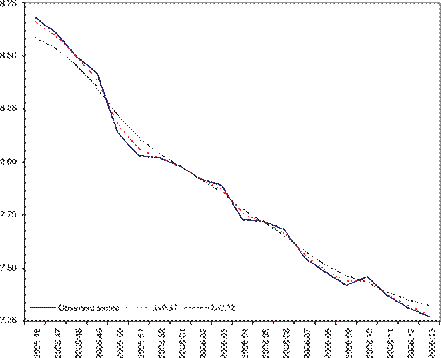
Figure 7. Weekly yield rate of CETES28 and trends with S%=65% (=0.37) and S%=85% (=2.32).

Table IV. Weekly yield rate of CETES28. Selected trend values with S%=85%.

Sample used for trend estimation