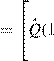Model-free evaluation of directional predictability in foreign exchange markets, страница 12

M_ZY1Y₂1,l,l ,l,l _ZY1Y21,l,lj/p/[,l,l]^1/2 21 jD1                

where

,l,l

 T2

,l,lj/pk² /p                                                                     dWudWv

j

and _,ju,_,ju, is the empirical generalized autocovariance function of fY_1t,Y_2tg,c Z_tc is the sample proportion for fY_1t > c,Y_2t > cg. All the M_ZY,l,l tests have the same N(0, 1) limit distribution as M_ZY

Once again, we conduct the stepwise testing procedure in a manner analogous to the previous case: we begin with a hypothesis test to check whether EZEZ_t, j D

0,š1,..., using the omnibus test statistic M_ZY1Y₂1,0,0. We then proceed to use the derivative tests M_ZY,l,l, for l D 1,2,3,4 to search possible sources of directional predictability of joint changes. Finally, we will use the M_ZZY1Z_Y21,0,0 test to examine whether the directions of past returns can be used to predict the direction of future joint changes.

We further perform the analyses via f_ZY1ω,u,v and f_ZY2ω,u,v, which will tell us whether the direction of joint changes in two currencies is predictable, using individual returns and

, respectively. Also, the same test procedures will be repeated for examining the direction of joint changes based on interest rate differentials, using two interest rate differential series j,ID jointly and individually. With these versatile test sets, we can better characterize the nature of directional predictability of joint changes in foreign exchange markets.

4.  DATA

Daily foreign exchange spot rates in currency units per US dollar and daily foreign currency futures prices for the Australia dollar (AD), the Canadian dollar (CD), the British pound (BP), the Japanese yen (JY), the Swiss franc (SF) and the Deutschemark (DM) are employed to examine directional predictability of the foreign exchange market. Foreign exchange spot rates are noon buying rates in New York for cable transfers payable and available from the Board of Governors of the Federal Reserve System (www.federalreserve.gov). Futures prices for the same six currencies, denoted by an F-prefix on each symbol, are daily closing prices traded at the Chicago Mercantile

¹⁹ The proof is a straightforward extension of that given in Hong and Chung (2006).

Exchange (CME) and obtained from Datastream. We compute returns as the percent logarithmic difference

Y_t/S_t,

where S_t is an exchange spot rate or futures price.^[15]

To construct interest rate differentials r_t  r_t^Ł, we use the 3-month London InterBank Offered Rate (LIBOR) for the US dollar (USD) and all six currencies as the domestic risk-free interest rate r_t and the foreign risk-free interest rate r_t^Ł, respectively. Daily observations on the interest rates come, when available, from Datastream.^[16] Table I reports descriptive statistics of the sample. The first two panels include some basic statistics for the returns on spot rates and futures prices, which have the same starting date, December 1 1987, but have different ending dates for DM. Upon the introduction of the euro and the irrevocably fixed conversion rates, the DM data stop after December 31 1998 and December 14 2001, respectively, for spot rates and future prices. Total observations in futures prices are slightly more than those in spot rates, due to different trading days in each market.

The sample means of returns are marginally different across currencies and markets (i.e., spot rates and futures prices), but they are all close to zero. CD is most stable for both spot and futures, with a standard deviation that is roughly half the size of other currencies. There is evidence of leptokurticity, but there is no clear evidence of negative skewness (particularly for FJY).^[17]