Model-free evaluation of directional predictability in foreign exchange markets, страница 10

∂u∂v

empirical generalized cross-covariance function between fZ_tcg and fY_tg, and ϕO_ZYj,u, T e^iuZtc is the empirical joint characteristic function of fZ_tc,Y. Here, kÐ is a kernel function, p  pT is a bandwidth,^[13] and the factor  is a finite sample correction factor for better finite sample performance.

Under the null hypothesis ₀ of no directional predictability, f_ZY^0,1,lω,0,v becomes a flat generalized cross-spectrum:

                                            fZY,0,10,lω,                                       ,       ω    ,]                                          11

2

which can be consistently estimated by

                                                           fO ZY,0,10,lω,ZY,00,v                                                       12

2

Thus, any significant difference between f_ZY^0,1,lω,0,v and f_ZY,^0,1₀^,lω,0,v will indicate evidence against ₀. Such a discrepancy can be measured by the quadratic norm between the estimators fO ZY0,1,lω,0,v and ,lω,:

                               T                jfO ZY0,1,lω,  f_ZY,0,1₀,lω,

T1

                                              j/pT                                                                                                  13

jD1

where WÐ is a positive and nondecreasing weighting function, and the unspecified integral is taken over the support of W Then, the resulting test statistic is a standardized version of the cumulative sum of :

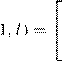
                                                                                             T1                     

                                 M_ZY                                                                   j/p/                           14

jD1

where the centering and scaling factors ,l and ,l are approximately the mean and the variance of the quadratic form TQ in (13) and their expressions are given in Hong and Chung (2006). Under ₀, the statistic MO _ZY1,l is asymptotically N(0, 1). It generally diverges to positive infinity under the alternatives to ₀, and thus allows us to use upper-tailed N(0, 1) critical values as appropriate critical values (see Hong and Chung, 2006, for details).

The last stage of our stepwise testing procedure is to examine whether the directions of past returns_j,j > 0g can be useful to predict the directions of future returns fZ_tg. This aims to explore a growing empirical evidence of pattern anomalies in foreign exchange markets, such as over/underreaction (e.g., Larson and Madura, 2001, and references therein) and long swing (Engel and Hamilton, 1990). The former indicates short-term price reversal (or continuation) following large price changes, while the latter presents periodic short-term foreign exchange rate movements in one direction. In a period of time where these pattern anomalies are found, the successive directions of foreign exchange rate movements can be examined as a function of past directions.

To capture serial dependence in the univariate time series fZ_tcg that consists of past and future directions, we use the generalized spectral density function of Hong (1999):

1

                                                       fZZω,u,                    ZZ,ju,veijω                                                                  15

2 jD1

where the generalized covariance function is

                                                                 ZZ,ju,coveiuZtc,ec                                                          16

The associated test statistic M_ZZ1,0 to test ₀ : EZ_t EZ_t a.s. can be derived in a similar manner to the test statistic M_ZY1,0: we compare a consistent kernel estimator for the (1, 0)th order univariate generalized spectral derivative f_ZZ^0,1,0ω,0,v and a consistent estimator for the flat spectrum f_ZZ,^0,1₀^,0ω,u, Likewise, the M_ZZ1,0 test has the same N(0, 1) limit distribution as M_ZY1,l (Hong, 1999).