Cистема координат на прямой и на плоскости. Расстояние между точками на осях координат, страница 4

4.  Точки пересечения прямой y=2х и окружности  (x - 1)² + (y - 2)² = 4  .

Вариант № 21

1.  Записать уравнение прямой с угловым коэффициентом.

2.  Фокусы гиперболы.

3.  Директриса параболы.

4.  Определить координаты точек пересечения с осями координат линии, заданной уравнением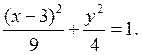

Вариант № 22

1.  Записать формулу для вычисления угла от прямой y = k₁x+b₁ до прямой y = k₂x+b₂ , отсчитанного против часовой стрелки.

2.  Фокус параболы.

3.  Найти центр и радиус окружности, заданной уравнением  x² + y² + 4x + 4 -|d|=0; (d ≠ 0).

4.  Точки пересечения прямой y=-x и параболы y=x².

Вариант № 23

1.  Записать общее уравнение прямой.

2.  Изобразить на координатной плоскости эллипс с центром в точке (0; 0), если длины его большой и малой полуосей равны a и b соответственно.

3.  Определить координаты точек пересечения с осями координат линии, заданной уравнением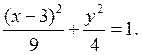

4.  Изобразить на координатной плоскости кривую, задающуюся уравнением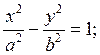   

Вариант № 24

1.  Записать каноническое уравнение эллипса.

2.  Дан треугольник с вершинами A(x₁; y₁), B(x₂; y₂) C(x₃; y₃). Написать уравнение сторон этого треугольника и формулы для вычисления их длин.

3.  Записать уравнение эллипса, центр которого смещен в точку O с координатами (x₀; y₀).

4.  Определить координаты точек пересечения с осями координат линии, заданной уравнением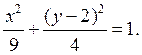

Вариант № 25

1.  Записать условие параллельности прямых y = k₁x+b₁ и y = k₂x+b₂.

2.  Фокусы эллипса.

3.  Записать уравнение гиперболы, центр которой смещен в точку C₀ с координатами (x₀; y₀).

4.  Определить координаты точек пересечения с осями координат линии, заданной уравнением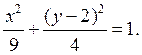

Вариант № 26

1.  Записать уравнение окружности с центром в точке M₀(x₀;y₀) и радиусом R. Изобразить на координатной плоскости кривую, задающуюся уравнением  x² = 2py.

2.  Эксцентриситет гиперболы.

3.  Определить координаты точек пересечения с осями координат линии, заданной уравнением

4.  Директриса параболы.

Вариант № 27

1.  Записать уравнение окружности с центром в точке M₀(x₀;y₀) и радиусом R.

2.  Фокусы эллипса.

3.  Записать уравнение эллипса, центр которого смещен в точку O с координатами (x₀; y₀).

4.  Определить координаты точек пересечения с осями координат линии, заданной уравнением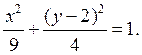

Вариант № 28

1.  Записать условие параллельности прямых y = k₁x+b₁ и y = k₂x+b₂.

2.  Дан треугольник с вершинами A(x₁; y₁), B(x₂; y₂) C(x₃; y₃). Написать уравнение сторон этого треугольника и формулы для вычисления их длин.

3.  Записать уравнение гиперболы, центр которой смещен в точку C₀ с координатами (x₀; y₀).

4.  Определить координаты точек пересечения с осями координат линии, заданной уравнением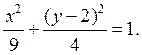

Вариант № 29

1.  Записать каноническое уравнение эллипса.

2.  Определить точки пересечения с осями координат линии, заданной уравнением

y=x² + 3x - 4.

3.  Эксцентриситет гиперболы.

4.  Дать определение эллипса.

Вариант № 30

1.  Записать уравнение прямой в отрезках на осях.

2.  Изобразить на координатной плоскости кривую, задающуюся уравнением  x² = 2py.

3.    Записать уравнения асимптот гиперболы.

4.    Определить координаты точек пересечения с осями координат линии, заданной уравнением

Вариант № 31

1.  Построить на координатной плоскости окружность с центром в начале координат и радиусом R. Записать её уравнение.