Высшая математика. 1-ый модуль. 1-ый семестр. 1-ый курс
1. Расстояния между двумя точками на осях координат и на плоскости.
2. Уравнение прямой с угловым коэффициентом.
3. Каноническое уравнение эллипса. Форма, свойства и построение эллипса.
4.
Является
ли прямоугольным треугольник с вершинами ![]() ,
,
![]() ,
,
![]() ?
?
1. Общee уравнение прямой. Уравнение осей координат.
2. Каноническое уравнение параболы. Свойства и форма параболы.
3. Область
определения ![]() для канонического
уравнения эллипса.
для канонического
уравнения эллипса.
4. Составить
уравнение гиперболы, для которой действительная полуось ![]() ,
эксцентриситет
,
эксцентриситет ![]() .
.
5. Составить
уравнение окружности с центром в точке![]() и
радиусом
и
радиусом ![]() .
.
6. Построить треугольник
с вершинами ![]() и составить
уравнение одной из его tвысот.
и составить
уравнение одной из его tвысот.
7. Найти
точки пересечения гиперболы ![]() с осями
координат и построить ее.
с осями
координат и построить ее.
1. Уравнение прямой с угловым коэффициентом.
2. Расстояние
между точками ![]() ,
,
![]() на
плоскости.
на
плоскости.
3. Определение, свойства и форма гиперболы. Каноническое уравнение гиперболы.
4. Построить
окружность с центром в точке ![]() и
радиусом
и
радиусом ![]() и
составить ее уравнение.
и
составить ее уравнение.
5. Найти
фокусы и эксцентриситет эллипса 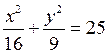 .
.
6. Дан
треугольник с вершинами ![]() . Составить
уравнение медианы
. Составить
уравнение медианы ![]() .
.
7.
Найти
точки пересечения линии ![]() и
координатных осей.
и
координатных осей.
1. Свойства фокусов и эксцентриситета эллипса.
2. Уравнeние прямой в отрезках на осях.
3. Виды парабол. Каноническое уравнение параболы.
4. Найти
точку пересечения окружности ![]() и
параболы
и
параболы ![]()
5. Найти угол между
прямыми ![]() .
.
6. Даны точки
![]() .Отрезок
.Отрезок ![]() разделить
точкой
разделить
точкой ![]()
в
отношении ![]()
7. Составить уравнение
гиперболы с полуосью ![]() и
эксцентриситетом
и
эксцентриситетом ![]() .
.
Высшая математика. 1-ый курс. 1-ый семестр. 1-ый модуль.
1. Деление отрезка на осях координат и на плоскости в заданном отношении.
2. Диаметры и вершины эллипса.
3. Фокус и директриса параболы.
4. Составить
уравнение прямой, проходящей через точки ![]() .
.
5. Найти
периметр треугольника с вершинами ![]() .
.
6. Найти
центр и радиус окружности ![]() .
.
7. Построить
гиперболу 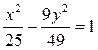 .
Составить уравнения её осей симметрии.
.
Составить уравнения её осей симметрии.
Высшая математика. 1-ый курс. Первый семестр. Первый модуль.
1. Угол между двумя прямыми на плоскости.
2. Деление отрезка в заданном отношении.
3. Определение и свойства параболы.
4. Для
эллипса малая ось ![]() равна
равна
![]() ,
а удвоенноерасстояние между фокусами
,
а удвоенноерасстояние между фокусами ![]() .
Составить уравнение эллипса и построить его.
.
Составить уравнение эллипса и построить его.
5. Составить
уравнение одной из высот треугольника с вершинами ![]()
6. Найти
центр и радиус окружности ![]()
7.
Построить
гиперболу 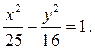 Найти
расстояние между её фокусами.
Найти
расстояние между её фокусами.
Высшая математика. 1-ый курс. 1-ый семестр.
1-ый модуль. Вариант №47
1. Виды уравнений окружности.
2. Каноническое уравнение параболы. Форма параболы.
3. Уравнeние прямой в отрезках на осях. Горизонтальне и вертикальне прямые.
4. Построить эллипс
![]() .
.
5. Найти
длину высоты ![]() треугольника
с вершинами
треугольника
с вершинами ![]() ,
,
![]() ,
,
![]() .
.
6. Построить
директрису параболы ![]()
7. Найти угол
между асимптотой гиперболы 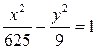 и
осью
и
осью ![]()
Высшая математика. 1-ый курс. 1-ый семестр.
1-ый модуль. Вариант №48
2. Виды уравнений окружности.
3. Уравнeние прямой с угловым коэффициентом.
4.
Построить
эллипс ![]() . Найти фокусы
и главные диметры эллипса.
. Найти фокусы
и главные диметры эллипса.
5.
Найти
длину высоты ![]() треугольника
с вершинами
треугольника
с вершинами ![]() ,
,
![]() ,
,
![]() .
.
6.
Составить
уравнение прямой, проходящей через точки ![]() и
и
![]() .
.
7. Принадлежит
ли асимптоте гиперболы 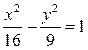 точка
точка
![]() ?
?
Высшая математика. 1-ый курс. Первый семестр.
Первый модуль. Вариант №49.
1. Определение и построение линий второго порядка на плоскости.
2. Уравнение прямой в отрезках на осях.
3. Директриса и фокус параболы.
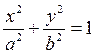 ,
для которой
,
для которой 5. Построить
гиперболу 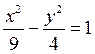 .
Составить уравнения её асимптот.
.
Составить уравнения её асимптот.
7. Найти точки
пересечения линии ![]() с
осями координат. Построить линию.
с
осями координат. Построить линию.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.