|
Высшая математика. 1-ый курс. Первый семестр. Первый модуль. Вариант №57. 1. Деление отрезка в заданном отношении. 2. Дать определение линии на плоскости. Уравнение линии. Принадлежность точки линии. 3. Угол между прямыми. Условия параллельности и перпендикулярности прямых. 4.
Составить
уравнение прямых, проходящих через точку 5.
Построить
окружность 6.
Построить эллипс 7.
Построить
гиперболу |
|
Высшая математика. 1-ый курс. Первый семестр. Первый модуль. Вариант №58 1. Уравнение прямой, проходящей через точки A(x1;y1) и B(x2;y2). 2. Уравнение окружности с центром в точке M0(x0;y0) и радиусом R. 3. Определение, свойства и построение гиперболы. 4. Найти
угол между двумя прямыми 5. Составить
уравнение эллипса с центром в точке 6. Построить
точки в отношении 7. Найти
расстояние от начала координат до прямой |
|
Высшая математика. 1-ый курс. Первый семестр. Первый модуль. Вариант №59 1. Свойства фокуса и директрисы параболы. 2. Угол между двумя прямыми на плоскости. 3. Координаты точки, делящей отрезок в заданном соотношении. 4. Составить
уравнение эллипса, для которого малая ось равна 2, а расстояние между
фокусами 5. Составить
уравнение окружности с центром в точке 6. Построить
гиперболу 7. Написать
уравнение прямой, проходящей через точки |
|
Высшая математика. 1-ый курс. Первый семестр. Первый модуль. Вариант №60 1. Уравнение прямой с угловым коэффициентом. 2. Отыскание точек пересечения линии с осями координат. 3. Определение параболы. Каноническое уравнение параболы. 4.
Построить
эллипс 5.
Построить
гиперболу 6.
Составить
уравнение прямой, проходящей через точки 7.
Найти
центр и радиус окружности |
|
Высшая математика. 1-ый курс. Первый семестр. Первый модуль. Вариант №61 1. Как задается система декартовых координат на прямой и на плоскости? 2. Уравнение
эллипса с центром, смещенным в точку 3. Определение и свойства модуля. Примеры. 4. Составить
уравнение прямой, проходящей через точки 5. Составить
уравнение директрисы параболы 6.
Найти
точку 7.
Построить
гиперболу |
|
Высшая математика. 1-ый курс. Первый семестр. Первый модуль. Вариант №62 1. Определение и свойства эллипса. 2. Каноническое уравнение гиперболы. 3. Виды и свойства парабол. Построение парабол. 4.
Найти
угол между двумя прямыми 5.
Определить
параметры и
составляющей с 6.
Построить
эллипс 7.
Дана
точка |
|
Высшая математика. 1-ый курс. Первый семестр. Первый модуль. Вариант №63 1. Область
определения 2. Директриса параболы. 3. Точки пересечения прямых. 4.
Найти
длину высоты 5.
Построить
гиперболу 6.
Построить
эллипс 7.
Составить
уравнение окружности с центром в точке Построить окружность. |
Высшая математика. 1-ый курс. Первый семестр.
Первый модуль. Вариант №64
1. Расстояния между точками на прямой и на плоскости.
2. Уравнение прямой, проходящей через две точки.
3. Эллипс. Его уравнение и свойства.
4. Даны
точки: точки ![]()
![]()
![]()
![]() Проверить,
Проверить,
что прямые ![]() и
и
![]() параллельны.
параллельны.
5. Найти
фокус параболы ![]() ..
..
6. Составить
уравнение окружности с центром в точке ![]() и
радиусом
и
радиусом ![]() . Найти
точки пересечения окружности с осями координат..
. Найти
точки пересечения окружности с осями координат..
7. Построить
гиперболу 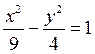 .
Найти ее эксцентриситет.
.
Найти ее эксцентриситет.
Высшая математика.1-ый курс. Первый семестр.
Первый модуль. Вариант №65.
1. Понятие модуля числа. Свойства модуля
2. Условия параллельности и перпендикулярности двух прямых.
3. Директриса и фокус параболы.
4. Найти центр и
радиус окружности ![]() .
Построить окружность.
.
Построить окружность.
5. Найти
периметр треугольника с вершинами ![]()
![]()
![]()
6. Построить
гиперболу 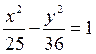 .
Найти ее эксцентриситет. Построить ее асимптоты.
.
Найти ее эксцентриситет. Построить ее асимптоты.
7. Даны точки
![]() . Найти
точку
. Найти
точку ![]() , делящую отрезок
, делящую отрезок
![]() в
отношении
в
отношении ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.