Выбор исполнительного двигателя. Расчет основных параметров редуктора. Построение механической характеристики исполнительного двигателя, страница 2

J_q =0– момент инерции редуктора.

.

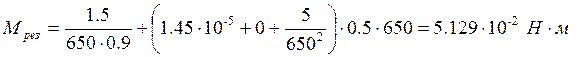M_П = > M_рез

2) Величина эквивалентного момента должна быть меньше номинального момента на валу исполнительного двигателя.

,

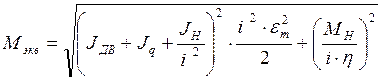М_{экв <} М_N=H*м

Результаты проверки показали, что выбранный двигатель удовлетворяет условиям пригодности исполнительного двигателя.

Предварительное передаточное число редуктора может быть не оптимальным с точки зрения быстродействия системы, следовательно, значение передаточного числа редуктора следует уточнить.

Построим графики зависимостей  (рис 1) и (рис. 2).

Область допустимых значений передаточного числа редуктора определятся уравнением:

Корни этого квадратного уравнения относительно i, получаем:

-  минимально значение передаточного числа  

-  максимально допустимое передаточное отношение

Для нахождения оптимального передаточного числа с точки зрения быстродействия системы нужно найти экстремум функции

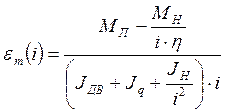
Эта функция имеет максимум в точке i = 1050 (см. рисунок 2), это передаточное отношение является наилучшим с точки зрения ускорения, но эта точка лежит правее точки i₀, при этом увеличивается инерционность редуктора и его массогабаритные показатели,  поэтому принимаем передаточное число i₀, которое было получено на предварительном этапе расчета.

а)

б)

Рис.1 - График зависимости : а – область допустимых значений; б – запретная область.

Рис.2 - График зависимости

3. Расчет основных параметров редуктора.

3.1 Число пар зубчатых колес.

Число пар зубчатых колес:

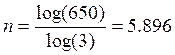
где:

i – передаточное отношение редуктора.

Передаточные числа первых двух пар выбираются в пределах 2-3, а третьей и последующих - в пределах 4-8.

Определение числа зубьев каждого колеса.

Разобьем передаточное число на передаточные числа отдельных пар зубчатых колес:    

Для определения числа зубьев колес нужно предварительно задаться числом зубьев ведущих колес, число зубцов ведомого колеса получается путем перемножения передаточного числа зубчатой на число зубцов ведущего колеса. При их выборе учитывается режим работы редуктора. Для увеличения надежности редуктора выберем многочасовой ежедневный режим работы. Где .

число зубцов шестеренок	число  зубцов колес
Z1 = 20	Z2 = 40
Z3 = 20	Z4 = 80
Z5 = 20	Z6 =80
Z7 = 20	Z8 = 80
Z9 = 20	Z10 = 100

 

3.2 Расчет модуля.

Расчет модуля производится для самой нагруженной ступени зубчатого механизма.

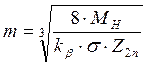, где:

k_b=0.4 - коэффициент ширины зуба;

- допустимое напряжение материала колеса при расчете на выносливость;

Z_2n=100 – число зубьев выходного колеса.

Выбранное значение модуля должно быть не меньше полученного, для обеспечения прочности зубчатого колеса. Значение модуля выбирается из нормального ряда регламентированного государственным стандартом. Выберем модуль, равный 1 мм.

3.3  Расчет диаметров зубчатых колес.

Диаметр каждого колеса вычисляется как произведение модуля на число зубьев:

                                 

                               

                              

                       

3.4 Расчет ширины колеса.

Ширина колеса рассчитывается как произведение коэффициента ширины зуба на модуль.

где: y =5 - коэффициент ширины зуба (4-10).

3.5 Момент инерции редуктора

Окончательно момент инерции создаваемый редуктором:

, где:  r- плотность материала колес(r =8000 кг/м³);

b– ширина колес.

После расчета момента инерции редуктора необходимо выполнить проверку выбранного двигателя с учетом инерционных свойств редуктора: