Совокупность значений результативного признака у и соответствующие им значения факторных признаков х1, х2, х3, страница 5

Уравнение  множественной корреляции будет выглядеть так:

y=0,039х₃+1,17x₂-2702.2

12. Расчет коэффициента множественной корреляции

= 0,92

Коэффициент множественной корреляции получился довольно высокий = 0,92, что говорит о тесной взаимосвязи между рассматриваемыми признаками.

13. Расчет ошибки коэффициента множественной корреляции

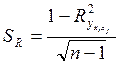
100% =4%

Допустимое значение ошибки не должно превышать 5%.

Значение ошибки составило 4%, что является нормой при допустимых 5%. Полученный результат говорит об адекватности проведенных расчетов и корректности полученных результатов.

14. Расчет совокупного коэффициента детерминации

Коэффициент детерминации характеризует долю дисперсии результативного признака, которая объясняется влиянием факторов, входящих в линейное уравнение регрессии и рассчитывается по следующей формуле:

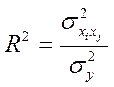, где

- дисперсия факторных признаков,

 - дисперсия результативного признака.

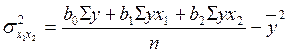= 4217062,467

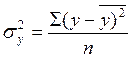= 4934666,7

Таким образом, коэффициент детерминации равен:

R² = 4217062,467/4934666,7 = 0,85

Вариации результативного признака на 85% объясняется вариацией факторов включенных в модель, то есть взаимосвязь исследуемых признаков высокая.

15. Проверка

Коэффициент множественной корреляции, возведенный в квадрат, должен равняться коэффициенту детерминации:

(0,92)²=0,85

0,85 = 0,85

16. Общий вывод

Проводя проверку однородности исследуемой совокупности пришли к выводу, что максимальное значение результативного признака - 11700 тыс. руб. Допустимые границы вариации признака от –979,3 тыс. руб. до 13879,3 тыс. руб. Из этого следует, что испытываемый элемент (а именно максимальное значение результативного признака = 11700 тыс. руб.) входит в расчетные пределы, поэтому исследуемая совокупность является однородной.

Полученные значения  коэффициента вариации свидетельствуют о том, что вариация признака у, х₂ и х_З - является однородной, так как коэффициент вариации меньше 33%.

Фактические данные результативного признака (при их проверки на нормальность по способу Вестергарада) свидетельствуют о достаточно близком распределении эмпирических данных к теоретическим нормального распределения.

Полученное, в результате расчетов, уравнение связи между товарной продукции лесозаготовок и удельными трудозатратами на лесозаготовках свидетельствует о линейной зависимости между этими признаками.

При определении линейной зависимости между двумя факторными признаками, связанными с результативным и имеющими наибольшее значение коэффициентов корреляции (0,97 и 0,958) получили следующее уравнение регрессии: y=0,039х₃+1,17x₂-2702.2

Значение коэффициента множественной корреляции равно 0,92, следовательно, связь между рассматриваемыми признаками достаточно тесная. Ошибка коэффициента множественной корреляции, равна 4, что  ниже допустимого значения - 5%, это является положительной чертой проводимого анализа.

Совокупный коэффициент детерминации - 0,85 или 85%, следовательно, вариации результативного признака на 85% объясняется вариацией факторов включенных в модель, то есть объем товарной продукции лесозаготовок зависит от удельных трудозатрат на лесозаготовках и от выработки товарной продукции на 1 работающего.