Совокупность значений результативного признака у и соответствующие им значения факторных признаков х1, х2, х3, страница 3

Вывод: расчеты показывают, что самое большое влияние на результативный признак оказывает факторный признак х₃, наименьшее – х₁.

7. Расчет квадратической ошибки коэффициента корреляции

Если совокупность относится к однородной и нормально-распределенной, то ошибку коэффициента корреляции можно вычислить по формуле:

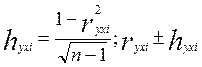
Таблица 6

8. Отбор факторных признаков

Определим факторный признак наиболее тесно связанный с результативным. Таковым признаком являются удельные трудозатраты на лесозаготовках (х3), так как коэффициент корреляции равен  0,97.

9. Нахождение и  статистическая оценка уравнения регрессии

Следует сделать предположение о линейной зависимости изучаемых признаков и записать уравнение линейной регрессивной зависимости:

Для определения параметров b₀  и b₁  в этом регрессивном уравнении надо решить следующую систему нормальных уравнений:

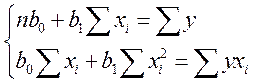
Чтобы получить коэффициент системы уравнений составим рабочую таблицу.

Таблица 7

х3	у	х3y	х32	у=b0+b1x3
350	3200	1120000	122500	2458,86
390	4000	1560000	152100	3535,14
440	4200	1848000	193600	4880,49
460	5400	2484000	211600	5418,63
480	5600	2688000	230400	5956,77
480	5800	2784000	230400	5956,77
510	6200	3162000	260100	6763,98
520	6400	3328000	270400	7033,05
520	7200	3744000	270400	7033,05
530	7400	3922000	280900	7302,12
540	7600	4104000	291600	7571,19
580	8600	4988000	336400	8647,47
590	9100	5369000	348100	8916,54
640	9600	6144000	409600	10261,89
640	11700	7488000	409600	10261,89
7670	102000	54733000	4017700	102000

Подставим в систему полученные данные:

15 * b₀ +  b₁ * 7670 = 102000

b₀ * 7670  +  b₁ * 4017700 = 54733000

Решив систему уравнения получаем:

b₀=-6958,59

b₁=26,907

Проведем проверку: =102000

Уравнение линейной регрессионной зависимости будет выглядеть так: