Совокупность значений результативного признака у и соответствующие им значения факторных признаков х1, х2, х3, страница 2

г) Определяем допустимые границы вариации признака. Итак, значения признака должны варьироваться в следующих пределах:

, то есть

Вывод: Таким образом, исключенный нами ранее максимальный элемент совокупности (11700) входит в допустимые пределы, значит рассматриваемая совокупность – однородна. Максимальный элемент будет рассматриваться нами в дальнейшем в составе изучаемой совокупности.

4. Рассчитаем показатели вариации результативного и факторного признаков.

Для этого рассчитаем средние арифметические, дисперсии, средние квадратические отклонения и коэффициенты корреляции признаков.

Используем следующие формулы:

а)  ,  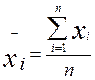  - средние арифметические простые;

б) , 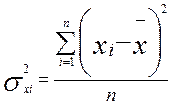-дисперсии;

в) , -средние квадратические отклонения значений результативного и факторного признаков от их средней;

г) 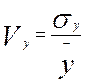*100, *100 - коэффициенты корреляции, показывающие удельный вес среднего квадратического отклонения в средней  величине признака.

Результаты расчетов представим в следующей таблице:

Таблица 3

Показатели вариации признаков

Показатели вариации	y	х1	х2	х3
	6800	292	8066,67	511,3
,	4934666,7	9922,67	1322888,9	6384,9
,	2221,41	99,6	1163,14	79,9
,%	32,67	34,1	14,4	15,6

Вывод: приведенные расчеты показали, что наиболее равномерная совокупность – это совокупность значений факторного признака х₂, поскольку коэффициент корреляции этого признака – самый низкий из рассчитанных (14,4%).

5. Проверка фактического распределения результативного признака на близость к нормальному. Эта проверка проводится по «способу Вестергарда», согласно которому, фактическое распределение данных можно считать близким к нормальному, если оно удовлетворяет следующим условиям:

а) если в интервале 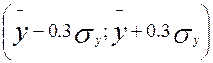 содержится 25% значений;

б) если в интервале 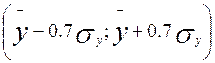 содержится 50% значений;

в) если в интервале 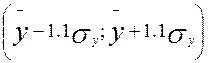содержится 75% значений;

г) если в интервале 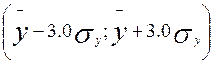 содержится 100% значений.

Оформим результаты проверки в таблице 4.

Таблица 4

Проверка фактического распределения результативного признака на близость к нормальному.

Интервалы (числовые данные)	Частота признака при распределении
	Нормальном		Фактическом
	абсолютном	относительном,%	абсолютном	относительном,%
(6133,21;7466,4)	4	25	4	25
(5235,1;8354,95)	8	50	8	50
(4356,4;9243,6)	11	75	10	66,7
(135,8;13464,23)	15	100	15	100

Вывод: распределение результативного признака можно условно считать близким к нормальному, так как оно по трем пунктам из четырех удовлетворяет условию «способа Вестергарда».

6. Отбор факторных признаков

Основание и отбор факторных признаков будем производить на основе симметричной матрицы линейных коэффициентов корреляции.

Коэффициент парной линейной корреляции можно рассчитать по следующей формуле:

 

Таблица 5