Воспуков И.В.
Содержание
1.Введение....................................................................................................... 3
2.Решение уравнения средствами MS Excel................................................... 4
2.1Построение графиков и уточнение корней............................................ 4
3.Решение уравнения средствами MathCAD.................................................. 8
3.1Построение графика, отделение и уточнение корней……..…………………8
4.Отделение корней уравнения на большом интервале [a1,b1], h1=0.1....... 9
4.1.Графическая иллюстрация..................................................................... 9
4.2.Текст программы на языке Pascal и результаты……….…………………...10
5.Уточнение корней уравнения методом секущих...................................... 11
5.1.Графическая иллюстрация................................................................... 11
5.2 Блок-схема алгоритма уточнения корней(метод секущих)................ 12
5.3.Текст программы на языке Pascal и результаты.................................. 13
6.Вывод...………………….………………………………………………………...15
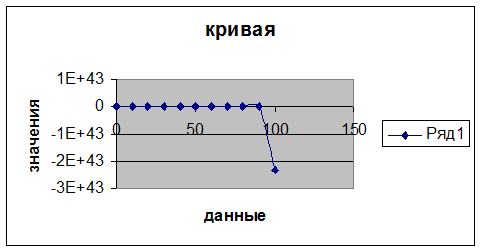
В среде табличного процессора Microsoft Excel отделить корни нелинейного уравнения вида ¦(х)=0 путем вычисления значений функции ¦(х). Построить ее график.
Решение:
Разбиваем данный интервал [0;100] на 10 равных промежутков. Т. к. на 0 делить нельзя, то за начало интервала возьмем число 0,000001.
|
0,000001 |
18,50865674 |
|
10 |
18485,1709 |
|
20 |
-197987210,6 |
|
30 |
-1,6484E+12 |
|
40 |
1,56987E+17 |
|
50 |
-5,00306E+21 |
|
60 |
1,08766E+26 |
|
70 |
-1,59308E+30 |
|
80 |
6,11614E+33 |
|
90 |
5,46831E+38 |
|
100 |
-2,31801E+43 |
-
 |
|
10 |
18485,1709 |
|
11 |
-261,6896166 |
|
12 |
-137338,0668 |
|
13 |
-401463,4805 |
|
14 |
-164437,7103 |
|
15 |
2483435,97 |
|
16 |
8509870,904 |
|
17 |
6646560,29 |
|
18 |
-43356371,88 |
|
19 |
-176466272,5 |
|
20 |
-197987210,6 |
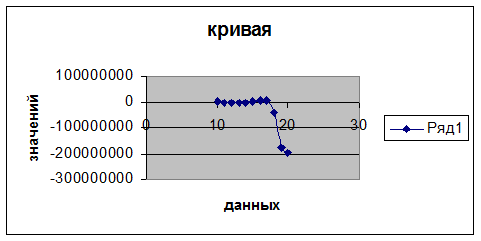
В выше полученной таблице корень лежит между 10 и 11, но не получена заданная точность, поэтому снова делим этот интервал на 10 частей:
|
|
18485,1709 |
|
10,1 |
19004,75918 |
|
10,2 |
19219,3925 |
|
10,3 |
19056,80863 |
|
10,4 |
18437,08405 |
|
10,5 |
17272,70435 |
|
10,6 |
15468,81794 |
|
10,7 |
12923,70808 |
|
10,8 |
9529,5213 |
|
10,9 |
5173,292533 |
|
11 |
-261,6896166 |
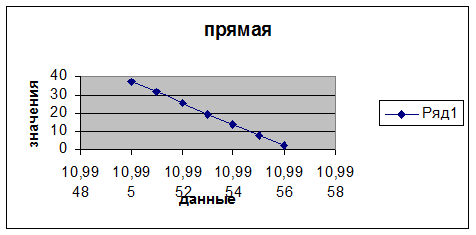
Заданная точность – 0,5*10-4, поэтому чтобы не делить многократно сразу возьмем значения близкие к заданной точности:
|
10,995 |
37,50918391 |
|
10,9951 |
31,55444955 |
|
10,9952 |
25,59852356 |
|
10,9953 |
19,64140582 |
|
10,9954 |
13,68309622 |
|
10,9955 |
7,723594628 |
|
10,9956 |
1,762900931 |
|
10,9957 |
-4,198984992 |
|
10,9958 |
-10,16206326 |
|
10,9959 |
-16,12633399 |
|
10,996 |
-22,0917973 |
|
10,9956 |
1,762900931 |
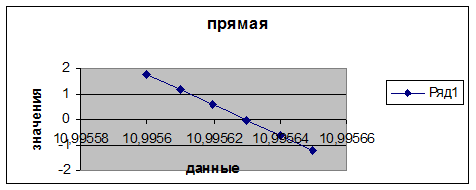 Откуда получаем
интервалы с заданной точностью:
Откуда получаем
интервалы с заданной точностью:
|
10,99561 |
1,166765991 |
|
10,99562 |
0,570619128 |
|
10,99563 |
-0,025539657 |
|
10,99564 |
-0,621710364 |
|
10,99565 |
-1,217892995 |
|
|
-1,6484E+12 |
|
31 |
-2,65722E+13 |
|
32 |
-6,58727E+13 |
|
33 |
2,84977E+12 |
|
34 |
4,95108E+14 |
|
35 |
1,43327E+15 |
|
36 |
5,51681E+14 |
|
37 |
-8,97E+15 |
|
38 |
-3,04248E+16 |
|
39 |
-2,30895E+16 |
|
40 |
1,56987E+17 |
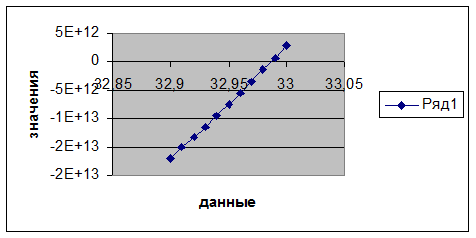
|
32,9 |
-1,6822E+13 |
|
32,91 |
-1,50359E+13 |
|
32,92 |
-1,32107E+13 |
|
32,93 |
-1,1346E+13 |
|
32,94 |
-9,4413E+12 |
|
32,95 |
-7,49622E+12 |
|
32,96 |
-5,51033E+12 |
|
32,97 |
-3,48321E+12 |
|
32,98 |
-1,41443E+12 |
|
32,99 |
6,96416E+11 |
|
33 |
2,84977E+12 |
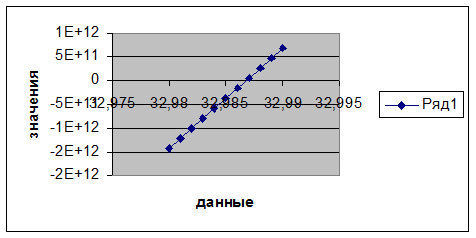
|
32,98 |
-1,41443E+12 |
|
32,981 |
-1,20525E+12 |
|
32,982 |
-9,95645E+11 |
|
32,983 |
-7,85617E+11 |
|
32,984 |
-5,75168E+11 |
|
32,985 |
-3,64296E+11 |
|
32,986 |
-1,53001E+11 |
|
32,987 |
58717433120 |
|
32,988 |
2,70859E+11 |
|
32,989 |
4,83425E+11 |
|
32,99 |
6,96416E+11 |
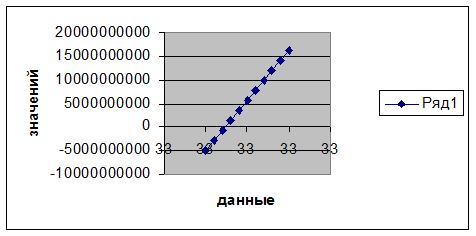 получаем
заданную точность:
получаем
заданную точность:|
32,9867 |
-4842494849 |
|
32,98671 |
-2724444888 |
|
32,98672 |
-606352567,5 |
|
32,98673 |
1511782117 |
|
32,98674 |
3629959163 |
|
32,98675 |
5748178574 |
|
32,98676 |
7866440347 |
|
32,98677 |
9984744486 |
|
32,98678 |
12103090989 |
|
32,98679 |
14221479855 |
|
32,9868 |
16339911089 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.