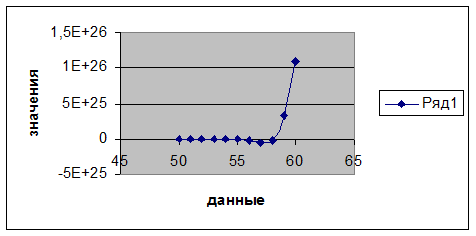
 Уточняем 3-ий корень
Уточняем 3-ий корень|
50 |
-5,00306E+21 |
|
51 |
-1,04595E+22 |
|
52 |
6,24419E+21 |
|
53 |
9,56278E+22 |
|
54 |
2,34757E+23 |
|
55 |
-1,70261E+22 |
|
56 |
-1,78465E+24 |
|
57 |
-5,11639E+24 |
|
58 |
-1,84198E+24 |
|
59 |
3,23947E+25 |
|
60 |
1,08766E+26 |
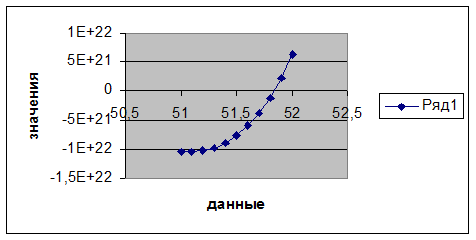
|
51 |
-1,04595E+22 |
|
51,1 |
-1,04596E+22 |
|
51,2 |
-1,02286E+22 |
|
51,3 |
-9,72025E+21 |
|
51,4 |
-8,88454E+21 |
|
51,5 |
-7,66741E+21 |
|
51,6 |
-6,01134E+21 |
|
51,7 |
-3,85574E+21 |
|
51,8 |
-1,13766E+21 |
|
51,9 |
2,20736E+21 |
|
52 |
6,24419E+21 |
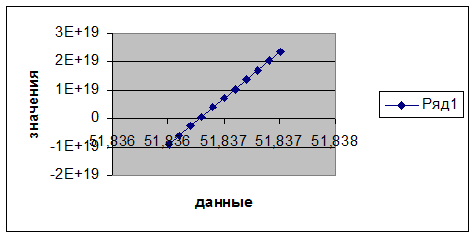
|
51,836 |
-9,06477E+18 |
|
51,8361 |
-5,81382E+18 |
|
51,8362 |
-2,56221E+18 |
|
51,8363 |
6,90046E+17 |
|
51,8364 |
3,94295E+18 |
|
51,8365 |
7,19651E+18 |
|
51,8366 |
1,04507E+19 |
|
51,8367 |
1,37056E+19 |
|
51,8368 |
1,69611E+19 |
|
51,8369 |
2,02172E+19 |
|
51,837 |
2,34741E+19 |
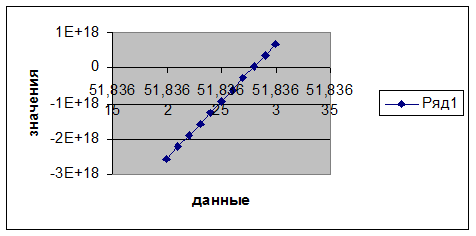 Получаем заданную точность:
Получаем заданную точность:|
51,8362 |
-2,56221E+18 |
|
51,83621 |
-2,23701E+18 |
|
51,83622 |
-1,91181E+18 |
|
51,83623 |
-1,5866E+18 |
|
51,83624 |
-1,26139E+18 |
|
51,83625 |
-9,36164E+17 |
|
51,83626 |
-6,10935E+17 |
|
51,83627 |
-2,857E+17 |
|
51,83628 |
3,95422E+16 |
|
51,83629 |
3,64791E+17 |
|
51,8363 |
6,90046E+17 |
3.1.Построение графика, уточнение и отделение корней
В пакете математических расчетов MathCad построить график функции ¦(х), отделить корни нелинейного уравнения ¦(х)=0 и уточнить значения корня, используя стандартные функции MathCad.
Решение:
Строим график функции: ¦(t)=ln(2/t)-et cos(t)+5, ¦(t)=0 ![]()
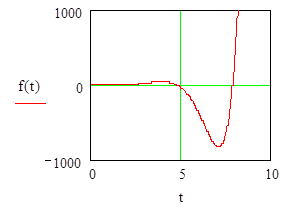
В точках, где график функции пересекает ось ОХ, будет решение данного уравнения. Далее с помощью функции root отделяем корни с заданной точностью. Т.е. вводим (приблизительно) значения точек пересечения графика с осью и заданную точность, получаем решение уравнения:
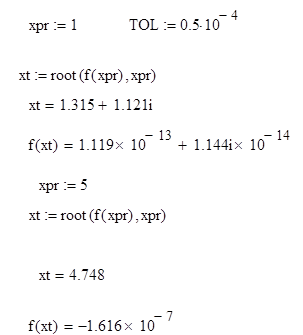
y=f(x)
 |
 y2
y2
y1


![]()
![]() ···
y2 b
···
y2 b
![]() a1
a b1
a1
a b1
 |
![]() ···
b a
···
b a
![]()
![]()
![]()
![]() h h y1
h h y1
![]()
![]()
![]()
![]()
![]()
![]() h h
h h
y1 y1
y1
рис. 1
Дано:
a1, b1, h, f(x)
Найти:
a, b
Пояснения:
f(x) – функция уравнения;
a1, b1 – большой интервал, внутри которого исследуются корни уравнения f(x)=0;
a, b – интервалы размером (шагом) h, внутри которых находятся корни уравнения;
y1 – значение функции уравнения в начале шага;
y2 – значение функции уравнения в конце шага.
Процесс нахождения интервалов [a, b] называется отделением корней уравнения.
4.2.Текст программы на языке Pascal и результаты
Program pasotd; отделение корней на большом интервале a1 -b1
Var a1,b1,y1,y2,x,h:real; fp:text;
Function f(t:real):real;
Begin f:=ln(2/x)-exp(x)*cos(x)+5;
End;
Begin
assign(fp,'rez_otd.txt'); Rewrite(fp); a1:=0; b1:=100; h:=0.1; writeln(fp,' Результат отделения корней'); writeln(fp,'на интервале [',a1:0:1,',',b1:0:1,'], h=',h:0:2); y1:=f(a1);
x:=a1;
Repeat x:=x+h; y2:=f(x); if y1*y2<0 then
Writeln(fp,'a=',x-h:0:3,' y(a)=',y1:0:6, ' b=',x:0:3,' y(b)=',y2:0:6);
y1:=y2;
Until x>b1; close(fp);
End.
[0.00001,100.0], h=0.10
a=4.700 y(a)=5.506595 b=4.800 y(b)=-6.508826
a=7.800 y(a)=-128.021630 b=7.900 y(b)=127.735189
a=10.900 y(a)=5172.804931 b=11.000 y(b)=-262.291015
![]()
 у
у
![]()

![]() x1 x2
b
x1 x2
b
![]()
![]()
![]() 0
X
0
X
x0=a
рис. 2
Пояснения:
Процесс уточнениякорней на отрезке [a,b] с точностью e методом секущих состоит в последовательном (в цикле) построения хорд-секущих до тех пор, пока расстояние между значениями [a, b] не станет меньше e (e=0,5*10-4). Корнем уравнения с точностью e является любое значение x, принадлежащее найденному отрезку [a, b].
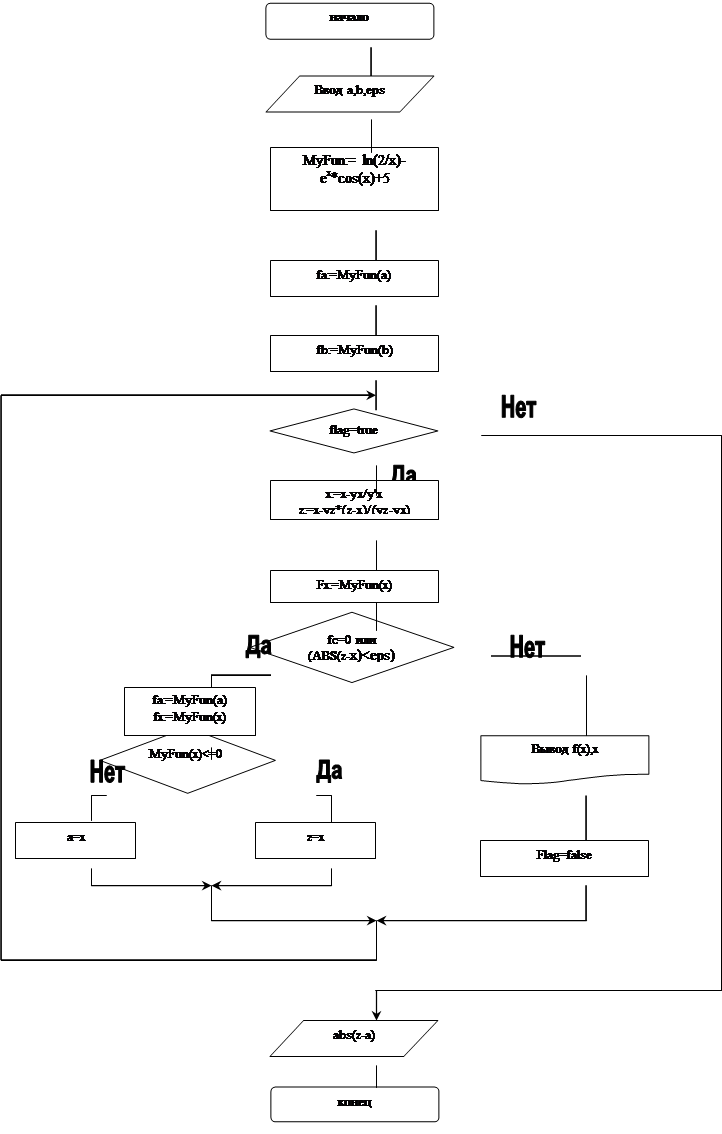 |
Program utompd; Уточнение корня методом полов.деления Var
x,yx,ya,a,b,eps:real;
fp:text;
Procedure f1(x:real; var y:real);
Begin y:=(ln2/x)-ex*cos(x)+5;
End;
Procedure f2(x:real; var y:real);
Begin assign(fp,'rez_ut1.txt'); Rewrite(fp);
write(' Введи a:'); readln(a);
write(' Введи b:'); readln(b);
write(' Введи eps:'); readln(eps);
if ((ln2/a)-ea*cos(a)+5)*(6/a4-2*ea*sin(a)>0 then
begin
x:=a;
z:=b;
end else
begin
x:=b;
z:=a;
end;
Repeat
f1(a,ya); f1(x,yx); f2(a,ya); f2(x,yx);
x:=x-((ln2/x)-ex*cos(x)+5)/(-2/ex-ex*cos(x)+ex*sin(x);
z:=x-yz(z-x)/(yz-yx);
Until abs(z-x)<eps;
Writeln(fp,'x=',x:0:6,' f(x)=',yx:0:6); close(fp);
End.
Результат уточнения корней:
x=4.746685, f(x)=5.50768; x=7.854434, f(x)=127.707004; x=11.006052, f(x)=5173.292532.
Вывод
Цель данной работы достигнута: приобретены навыки по использованию и приложению табличного процессора Microsoft Excel, математического пакета MathCad, и языка программирования Pascal.
Анализируя результаты работы, можно сделать вывод о том, что наиболее простым и удобным способом уточнения и отделения корней уравнения является математический пакет MathCad, т.к. в Pascal и Excel эта процедура весьма трудоемка. В целом использование пакета MathCad является наиболее рациональным, простым и доступным для понимания при решении инженерных задач.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.