Линейная алгебра. Матрицы. Диагональная и квадратная матрица

Аннотация лекции. Лекция посвящена теме «Линейная алгебра». Введено понятие матрицы. Рассмотрены операции над матрицами и их основные свойства. Приведены примеры, иллюстрирующие эти свойства и понятия.

Линейная алгебра

Матрицы

Матрица размера m х n – это прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Матрицы принято обозначать заглавными латинскими буквами, а элементы – теми же, но строчными буквами с двойной индексацией. 

Например, рассмотрим матрицу А размерности 2 х 3:

 3     0        1 А  0      1,5     5 

В этой матрице две строки (m = 2) и три столбца (n = 3), т.е. она состоит из шести элементов a_ij, где i - номер строки, j - номер столбца. При этом i принимает значения от 1

до 2, а j от одного до трех (записывается i 1,2, j 1,3). А именно, a₁₁= 3; a₁₂= 0; a₁₃= -1; a₂₁= 0; a₂₂= 1,5; a₂₃= 5.

Матрицы А и В одного размера (m х n ) называют равными, если они поэлемент-

но совпадают, т.е. a_ij = b_ij для i 1,m, j 1,n , т.е. для любых i и j (можно записать i, j).

Матрица-строка – это матрица, состоящая из одной строки, а матрица-столбец – это матрица, состоящая из одного столбца.

Например, А2 0 6- матрица-строка, а B ^_75_ .

_

Квадратная матрица n-го порядка – это матрица, в которой число строк равно числу столбцов и равно n.

                                                     3   2

               Например, А ^5 5^_- квадратная матрица второго порядка.

Диагональные элементы матрицы – это элементы, у которых номер строки равен номеру столбца (a_ij, i = j). Эти элементы образуют главную диагональ матрицы. В предыдущем примере главную диагональ образуют элементы a₁₁= 3 и a₂₂= 5.

Диагональная матрица – это квадратная матрица, в которой все недиагональные

9 0 0

                                                                                                    

элементы равны нулю. Например, А^0 3 ⁰ - диагональная матрица третьего по0 0 1

рядка. Если при этом все диагональные элементы равны единице, то матрица называется

Матрица называется нулевой, если все ее элементы равны нулю.

Квадратная матрица называется треугольной, если все ее элементы ниже (или

Над матрицами можно производить следующие операции:

1.  Умножение матрицы на число. Произведением матрицы А на число  называется матрица В = А, элементы которой b_ij = a_ij для любых i и j.

                                                              3   2                 3    2 15    10

Например, если А 5  5_^{, то} 5*А _5        5__25       25_ . _

2.  Сложение матриц. Суммой двух матриц А и В одинакового размера m х n называется матрица С = А + В, элементы которой с_ij = a_ij + b_ij для i, j.

                                                                3   2       2   1

               Например, если А 5 5,B 0      1, то 

        C  А B _5302  55 5211_ 63___55                      63_.

_ Отметим, что через предыдущие операции можно определить вычитание матриц одинакового размера: разность А-В = А + (-1)*В.

3. Умножение матриц. Произведением матрицы А размера m x n на матрицу В размера n x p называется такая матрица С, каждый элемент которой с_ij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца мат-

n

рицы В, т.е. cij  ai1b1j  ai2b2j ...  ainbnj aikbkj .

k1

Например, если 

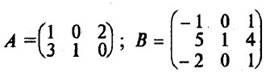, то размер матрицы-произведения будет 2 x 3, и она будет иметь вид: 

На основе операции умножения для квадратных матриц определена операция возведения в степень. Целой положительной степенью А^m (m > 1) квадратной матрицы А называются произведение m матриц, равных А, т.е.  А^m  A1*44A2*...4*43A

m раз

Подчеркнем, что сложение (вычитание) и умножение матриц определены не для любых двух матриц, а только для удовлетворяющим определенным требованиям к своей размерности. Для нахождения суммы или разности матриц их размер обязательно должен быть одинаковым. Для нахождения произведения матриц число столбцов первой из них должно совпадать с числом строк второй (такие матрицы называют согласованными). Возведение в степень определено только для квадратных матриц