











2. Лабораторная работа № 2
ЭЛЕКТРИЧЕСКИЕ цепИ синусоидального тока
Электрическими цепями синусоидального тока называются цепи, находящиеся под воздействием напряжения или тока синусоидальной формы (гармонического воздействия - ГВ). Как воздействие, так и все процессы (напряжения и токи) в такой цепи описываются синусоидальными функциями:
![]() (2.1)
(2.1)
где v(t) – мгновенное значение процесса (тока i(t) или напряжения u(t)); Vm – амплитуда (Um или Im); ω = 2πf = 2π/T – угловая частота (рад/с), а f и T – соответственно частота (Гц) и период (с); ωt и ψ – соответственно текущая и начальная фаза (рад или град); Φ(t) = ωt + ψ – полная фаза гармонического процесса (рад или град).
 |
Помимо амплитудного значения периодические ток и
напряжение также характеризуются действующим (среднеквадратичным) значением V (тока или напряжения). Действующий ток (напряжение)
численно равен такому постоянному току (напряжению), при котором за время,
равное одному периоду периодического воздействия, в проводнике с сопротивлением
R выделяется такое же количество тепловой энергии, как
и при переменном токе (напряжении). Действующие значения для синусоидальных
процессов в ![]() раз меньше амплитудных.
раз меньше амплитудных.
![]() (2.2)
(2.2)
 Описание синусоидальных процессов в
виде (2.1) и соответствующие им временные диаграммы просты и наглядны, однако
пользоваться ими при расчетах неудобно. Расчет цепей синусоидального тока
облегчается, если перейти к описанию процессов векторами на комплексной
плоскости (или комплексными числами) и использовать комплексный метод расчета.
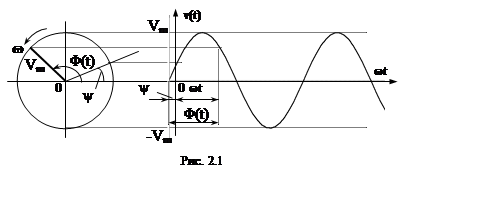
На рис. 2.2 на комплексной плоскости показан вектор
Описание синусоидальных процессов в
виде (2.1) и соответствующие им временные диаграммы просты и наглядны, однако
пользоваться ими при расчетах неудобно. Расчет цепей синусоидального тока
облегчается, если перейти к описанию процессов векторами на комплексной
плоскости (или комплексными числами) и использовать комплексный метод расчета.
На рис. 2.2 на комплексной плоскости показан вектор ![]() гармонического
воздействия вида (2.1). Комплексная величина
гармонического
воздействия вида (2.1). Комплексная величина![]() (в
литературе используется термин «текущий комплекс») определяет мгновенное
текущее значение синусоидальной функции v(t) и, как любое комплексное число, может быть представлено в
трех формах (рис. 2.2):
(в
литературе используется термин «текущий комплекс») определяет мгновенное
текущее значение синусоидальной функции v(t) и, как любое комплексное число, может быть представлено в
трех формах (рис. 2.2):
алгебраической:
![]() ;
(2.3)
;
(2.3)
тригонометрической:
![]() , (2.4)
, (2.4)
где ![]()
показательной:
![]() , (2.5)
, (2.5)
где ![]() .
.
Величину ![]() называют комплексной
амплитудой (комплексом) ГВ (вектор
называют комплексной
амплитудой (комплексом) ГВ (вектор![]() показан
на рис. 2.2). Она несет информацию только об амплитуде
показан
на рис. 2.2). Она несет информацию только об амплитуде ![]() и
начальной фазе ψ синусоидального воздействия, что при известной частоте ω
достаточно для описания синусоидального процесса и анализа свойств
электрической цепи при гармоническом воздействии.
и
начальной фазе ψ синусоидального воздействия, что при известной частоте ω
достаточно для описания синусоидального процесса и анализа свойств
электрической цепи при гармоническом воздействии.
Очевидно, что мгновенное значение v(t) и комплексная амплитуда связаны соотношением:
![]() .
(2.6)
.
(2.6)
Рассмотрим реакцию пассивных идеализированных элементов на гармоническое воздействие.
Резистивный элемент. Пусть через резистор с сопротивлением R протекает ток i(t) = Im sin(ωt + ψi). Тогда в соответствие с законом Ома падение напряжения на сопротивлении R равно
![]() (2.7)
(2.7)
Из (2.10) следует, что синусоидальные ток и напряжение на резистивном элементе совпадают по фазе, а амплитуда напряжения равна UmR = R∙Im.
Емкостной элемент. Напряжение на емкости C при протекании через нее синусоидального тока i(t) определяется по формуле
![]() (2.8)
(2.8)
где ψi - π/2 = ψu – начальная фаза напряжения на конденсаторе, а величина 1/ωС = xC (Ом) – сопротивление емкости С на частоте ω.
Из (2.11) следует, что напряжение на конденсаторе отстает по фазе от протекающего через него тока на угол φ = -π/2, а амплитуда синусоидального напряжения равна UmC = Im/(ωС) = xC·Im.
Индуктивный элемент. Напряжение на индуктивности равно
![]() (2.9)
(2.9)
где ψi + π/2 = ψu – начальная фаза напряжения на индуктивности, а величина ωL = xL (Ом) – сопротивление индуктивности L на частоте ω.
Следовательно, напряжение на индуктивности опережает по фазе ток на угол φ = π/2, а амплитуда UmL = ωL·Im = xL·Im.
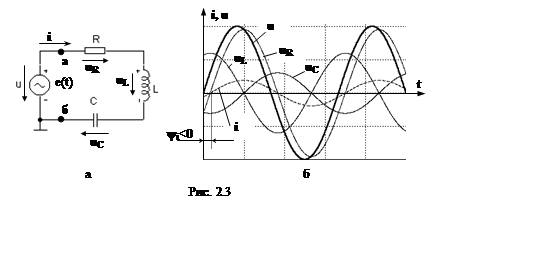
На рис. 2.3, а изображена электрическая цепь, состоящая из трех последовательно
соединенных пассивных элементов R, L
и C (последовательный контур), к которой
приложен синусоидальный источник э.д.с. e(t) = u(t).
Эпюры тока в цепи и напряжений на элементах цепи, полученные с помощью
программы Micro-Cap, приведены
на рис. 2.3, б. Они показывают, что синусоида напряжения на сопротивлении uR совпадает по фазе с синусоидой протекающего
тока i, а синусоиды uC
и uL сдвинуты относительно синусоиды тока i на угол π/2 соответственно вправо (отставание) и влево
(опережение). Между собой напряжения uC и uL находятся в противофазе. Как видно из рис. 2.4,
б начальная фаза входного напряжения u(t) равна нулю (ψu =
0), а фаза входного тока ψi < 0, поэтому
фазовый сдвиг между напряжением и током φ = ψu
– ψi >0, т.е. приложенное к цепи
синусоидальное напряжение u(t)
опережает по фазе протекающий в цепи ток на угол φ.
На основании 2-го закона Кирхгофа для схемы рис. 2.4 запишем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.